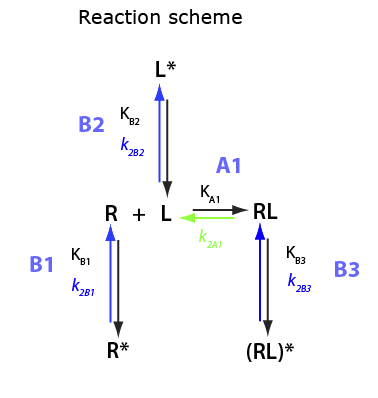
U-R-L-RL
Analysis of equilibrium thermodynamic equations for U-R-L-RL system: isomerization in both reactants and in the complex.

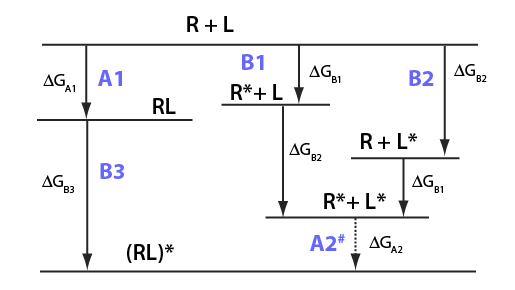
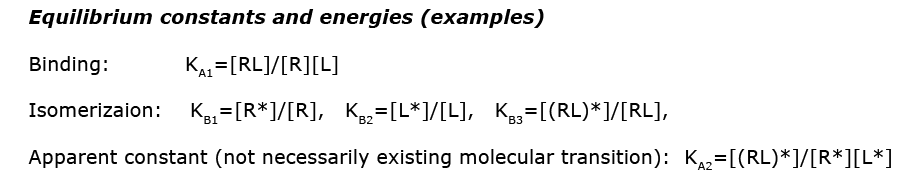
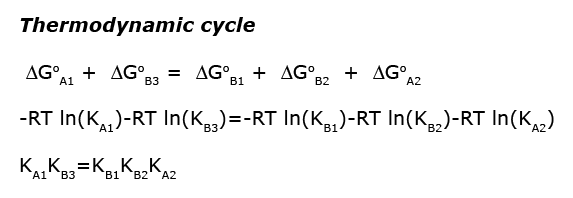
Images from: /Users/kovrigin/Documents/Workspace/Global Analysis/code_development/Mathematical_models/Equilibrium thermodynamic models/U-R-L-RL/U-R-L-RL.ai
Here I will analyze numeric solutions I derived in U-R-L-RL_derivation.mn.
Clean up
reset()
Path to previous results
ProjectName:="U-R-L-RL";
CurrentPath:="/Users/kovrigin/Documents/Workspace/Global Analysis/code_development/Mathematical_models/Equilibrium_thermodynamic_models/U-R-L-RL/"
![]()

Read results of derivations
filename:=CurrentPath.ProjectName.".mb";
fread(filename,Quiet):
anames(User)


Assume some values for testing operation
Total_R:=1e-3:
Total_L:=10e-3:
Ka1:=1e3:
Kb1:=1:
Kb2:=2:
Kb3:=5:
test operation of all functions
fLeq_U_R_L_RL(Total_R, Total_L, Ka1, Kb1, Kb2, Kb3);
fReq_U_R_L_RL(Total_R, Total_L, Ka1, Kb1, Kb2, Kb3);
fRstareq_U_R_L_RL(Total_R, Total_L, Ka1, Kb1, Kb2, Kb3);
fLstareq_U_R_L_RL(Total_R, Total_L, Ka1, Kb1, Kb2, Kb3);
fRLeq_U_R_L_RL(Total_R, Total_L, Ka1, Kb1, Kb2, Kb3);
fRLstareq_U_R_L_RL(Total_R, Total_L, Ka1, Kb1, Kb2, Kb3);
![]()
![]()
![]()
![]()
![]()
![]()
=> operative
Make wrapper functions for plotting
fLeq:=LRratio -> fLeq_U_R_L_RL (Total_R, LRratio*Total_R, Ka1, Kb1, Kb2, Kb3):
fReq:=LRratio -> fReq_U_R_L_RL (Total_R, LRratio*Total_R, Ka1, Kb1, Kb2, Kb3):
fRstareq:=LRratio -> fRstareq_U_R_L_RL (Total_R, LRratio*Total_R, Ka1, Kb1, Kb2, Kb3):
fLstareq:=LRratio -> fLstareq_U_R_L_RL (Total_R, LRratio*Total_R, Ka1, Kb1, Kb2, Kb3):
fRLeq:=LRratio -> fRLeq_U_R_L_RL (Total_R, LRratio*Total_R, Ka1, Kb1, Kb2, Kb3):
fRLstareq:=LRratio -> fRLstareq_U_R_L_RL(Total_R, LRratio*Total_R, Ka1, Kb1, Kb2, Kb3):
Test plotting
Total_R:=1e-3:
LRratio_max:=2:
Ka1:=1e6:
Kb1:=1:
Kb2:=2:
Kb3:=5:
LineW:=1.5: //line width
// create plots
pLeq:= plot::Function2d(
Function=(fLeq),
LegendText="[L]",
Color = RGB::Blue,
XMin=(0),
XMax=(LRratio_max),
XName=(LRratio),
TitlePositionX=(0),
LineWidth=LineW):
pRLeq:= plot::Function2d(
Function=(fRLeq),
LegendText="[RL]",
Color = RGB::Red,
XMin=(0),
XMax=(LRratio_max),
XName=(LRratio),
TitlePositionX=(0),
LineWidth=LineW):
plot(pLeq, pRLeq, LegendVisible=TRUE)
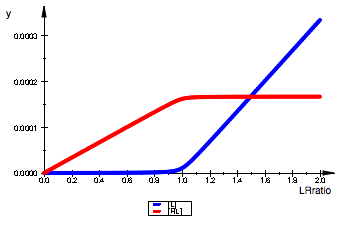
=> works
Assume some constants and evaluate titrations
Total_R:=1e-3:
Ka1:=1e5:
Kb1:=1e-5:
Kb2:=1e-5:
Kb3:=2:
LRratio_max:=1.5: // plotting range
LineW:=1.5: // plot line width
pLeq:= plot::Function2d(
Function=(fLeq),
LegendText="[L]",
Color = RGB::Blue,
XMin=(LRratio_max*1e-6),
XMax=(LRratio_max),
XName=(LRratio),
TitlePositionX=(0),
LineWidth=LineW):
pReq:= plot::Function2d(
Function=(fReq),
LegendText="[R]",
Color = RGB::Black,
XMin=(LRratio_max*1e-6),
XMax=(LRratio_max),
XName=(LRratio),
TitlePositionX=(0),
LineWidth=LineW):
pLstareq:= plot::Function2d(
Function=(fLstareq),
LegendText="[L*]",
Color = RGB::Green,
XMin=(LRratio_max*1e-6),
XMax=(LRratio_max),
XName=(LRratio),
TitlePositionX=(0),
LineWidth=LineW):
pRstareq:= plot::Function2d(
Function=(fRstareq),
LegendText="[R*]",
Color = RGB::Grey,
XMin=(LRratio_max*1e-6),
XMax=(LRratio_max),
XName=(LRratio),
TitlePositionX=(0),
LineWidth=LineW):
pRLeq:= plot::Function2d(
Function=(fRLeq),
LegendText="[RL]",
Color = RGB::Red,
XMin=(LRratio_max*1e-6),
XMax=(LRratio_max),
XName=(LRratio),
TitlePositionX=(0),
LineWidth=LineW):
pRLstareq:= plot::Function2d(
Function=(fRLstareq),
LegendText="[(RL)*]",
Color = RGB::Magenta,
XMin=(LRratio_max*1e-6),
XMax=(LRratio_max),
XName=(LRratio),
TitlePositionX=(0),
LineWidth=LineW):
// Text report
print(Unquoted,"Model: ".ProjectName);
print(Unquoted,"Total_R=".Total_R);
Kda1:=1/Ka1:
print(Unquoted,"Ka1=".Ka1." 1/M, Kd1=".Kda1." M");
Kdb1:=1/Kb1:
print(Unquoted,"Kb1=".Kb1." 1/M");
Kdb2:=1/Kb2:
print(Unquoted,"Kb2=".Kb2." 1/M");
Kdb3:=1/Kb3:
print(Unquoted,"Kb3=".Kb3." 1/M");
// plot all together
plot(pLeq, pReq, pLstareq, pRstareq, pRLeq, pRLstareq,
YAxisTitle="[X]", Header=("Model: ".ProjectName),
Height=160, Width=100,TicksLabelFont=["Helvetica",12,[0,0,0],Left],
AxesTitleFont=["Helvetica",14,[0,0,0],Left],
XGridVisible=TRUE, YGridVisible=TRUE,
LegendVisible=TRUE, LegendFont=["Helvetica",14,[0,0,0],Left],
ViewingBoxYMax=Total_R);
Model: U-R-L-RL
Total_R=0.001
Ka1=100000.0 1/M, Kd1=0.00001 M
Kb1=0.00001 1/M
Kb2=0.00001 1/M
Kb3=2 1/M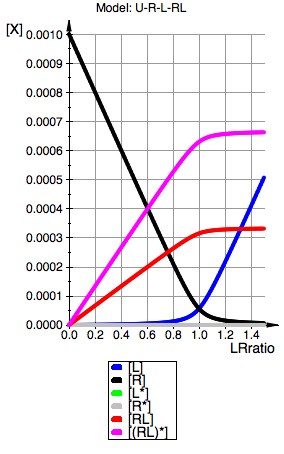
Jump back to the beginning of simulation section
Jump back to the beginning of simulation section
Test of the model: titration of R with L
Full model
|
Reduce to U |
Reduce to U-R |
Reduce to U-L |
Reduce to U-RL |
|
Model: U-R-L-RL |
Model: U-R-L-RL |
Model: U-R-L-RL |
Model: U-R-L-RL |
|
Reduce to U-R-L |
Reduce to U-R-RL |
Reduce to U-L-RL |
Full model U-R-L-RL |
|
Model: U-R-L-RL |
Model: U-R-L-RL |
Model: U-R-L-RL |
Model: U-R-L-RL |
Conclusion:
The model works as expected