ProjectName:="LRIM_U_R";
CurrentPath:="/Users/kovrigin/Documents/Workspace/Data/Data.XV/EKM16.Analysis_of_multistep_kinetic_mechanisms/Equilibria/";
![]()
![]()
Analysis of U-R model
A: R + L <=> RL
B: R <=> R*
2. Derivation of working equation
3. Express concentrations of equilibrium species in terms of a found solution
4. Define functions for equilibrium concentrations
5. Test if solution is meaningful
6. Check whether the solution satisfies all initial equation and conditions
7. Save results on disk for future use
In this notebook I will write out equations for equilibrium concentrations and either solve them or generate expressions for numeric solutions for a number of models derived in /Users/kovrigin/Documents/Workspace/Data/Data.XV/EKM16.Analysis_of_multistep_kinetic_mechanisms/LRIM/Specific_models/Models.pdf
clean up workspace
reset()
Set path to save results into:
ProjectName:="LRIM_U_R";
CurrentPath:="/Users/kovrigin/Documents/Workspace/Data/Data.XV/EKM16.Analysis_of_multistep_kinetic_mechanisms/Equilibria/";
![]()
![]()
Binding constants:
All binding constants I am using are formation constants so I denote them all as Ka and add a label for the transition.
K_a_A
K_a_A;
assume(K_a_A >= 0):
assumeAlso(K_a_A, R_):
![]()
K_a_B - Monomer-Ligand complex formation constant
K_a_B;
assumeAlso(K_a_B>=0):
assumeAlso(K_a_B,R_):
![]()
Total concentrations
Rtot - total concentration of the receptor
Rtot;
assumeAlso(Rtot>=0):
assumeAlso(Rtot,R_):
![]()
Ltot - total concentration of a ligand
Ltot;
assumeAlso(Ltot>=0):
assumeAlso(Ltot,R_):
![]()
Common equilibrium concentrations
Req - equilibrium concentration of a receptor monomer
Req;
assumeAlso(Req>=0):
assumeAlso(Req<=Rtot):
assumeAlso(Req,R_):
![]()
Leq - equilibrium concentration of a receptor monomer
Leq;
assumeAlso(Leq>=0):
assumeAlso(Leq<=Ltot):
assumeAlso(Leq,R_):
![]()
RLeq - equilibrium concentration of a receptor monomer
RLeq;
assumeAlso(RLeq>=0):
assumeAlso(RLeq<=Rtot):
assumeAlso(RLeq,R_):
![]()
Other species will be defined in the sections of specific models.
anames(All,User);
anames(Properties,User);

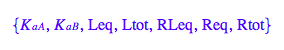
2. Derivation of working equation
U-R is a model with a receptor isomerization such that only one of the isomers binds ligand.
A: R + L <=> RL
B: R <=> R*
Working equation: I will try to express analytical [L] from equation for a total concentration of a receptor or use it for numeric solution if analytical is not possible
[R*] - equilibrium concentration of a receptor non-binding isomer
Rstareq;
assumeAlso(Rstareq>=0):
assumeAlso(Rstareq<=Rtot):
assumeAlso(Rstareq,R_):
![]()
Total concentrations of protein and a ligand
eq2_1:= Rtot = Req + Rstareq + RLeq;
eq2_2:= Ltot = Leq + RLeq;
![]()
![]()
Transition A: Equilibrium constant of ligand binding
eq2_3:= K_a_A = RLeq / (Req*Leq);
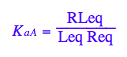
Transition B: Equilibrium constant of isomerization
eq2_4:= K_a_B = Rstareq/Req;
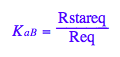
Let's get rid of [R*]
solve(eq2_4,Rstareq);
eq2_5:= Rstareq = %[2][1]
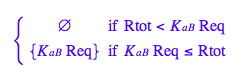
![]()
Let's get rid of [R]
solve(eq2_3,Req);
eq2_6:= Req = %[2][1]
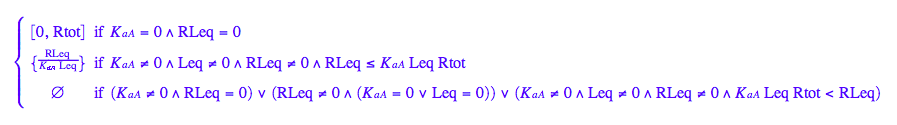
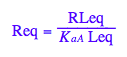
Let's get rid of [RL]
solve(eq2_2,RLeq);
eq2_7:= RLeq = %[2][1]

![]()
Substitute
eq2_1 | eq2_5;
% | eq2_6;
% | eq2_7;
eq2_8:= %;
![]()
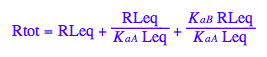
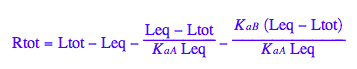
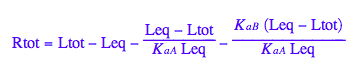
Final equation for [L] in terms of all constants
eq2_8

For the sake of my speed - use numerical solutions leaving analytical for future analysis.
Solve it for [L]
solutions2:=solve(eq2_8, Leq)

Extract solutions
eq2_9:= solutions2[i,1] $ i=1..nops(solutions2);
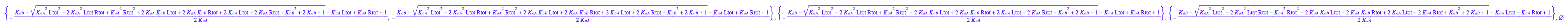
Is Eq2.9[1] a set of Eq2.9[2] and Eq2.9[3]?
if eq2_9[2][1] in eq2_9[1]
then print(Unquoted,"First set of roots contains the second root.");
else print(Unquoted,"First set of roots DOES NOT contain the second root!");
end_if;
if eq2_9[3][1] in eq2_9[1]
then print(Unquoted,"First set of roots contains the third root.");
else print(Unquoted,"First set of roots DOES NOT contain the third root!");
end_if;
First set of roots contains the second root.
First set of roots contains the third root.
Check correctness of the solutions by substitution into original equation to be solved:
Check first root
test1:= eq2_8 | Leq=eq2_9[2][1];
test2:=normal(test1);
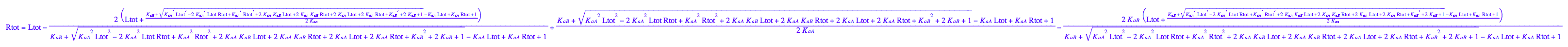
![]()
Check the second root
test1:= eq2_8 | Leq=eq2_9[3][1];
test2:=normal(test1);

![]()
3. Express concentrations of equilibrium species in terms of a found solution
Select one solution out of two found (check it below for being right one).
solution:=3
![]()
Equilibrium concentration of L :
eq3_1:= Leq= eq2_9[solution][1];
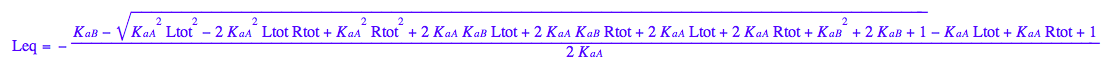
Equations for equilibrium concentrations
eq2_5; eq2_6; eq2_7
![]()
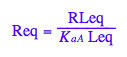
![]()
[RL]
eq3_2:= eq2_7 | eq3_1;
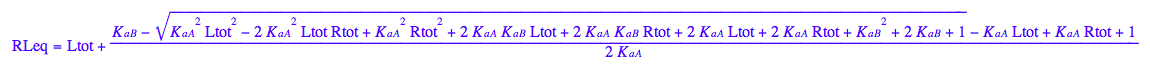
[R]
eq3_3:= eq2_6 | eq2_7 | eq3_1;

[R*]
eq3_4:= eq2_5 | eq3_3

Summary of equations for equilibrium concentrations:
eq3_1

eq2_7;eq3_2
![]()

eq2_6; eq3_3
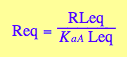

eq2_5; eq3_4
![]()

4. Define functions for equilibrium concentrations
fLeq:=(Rtot, Ltot, K_a_A, K_a_B) --> eq3_1[2]
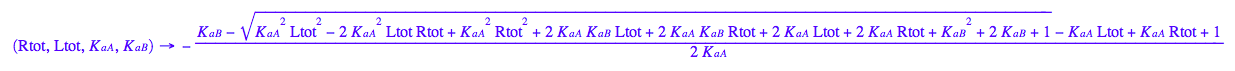
fReq:=(Rtot, Ltot, K_a_A, K_a_B) --> eq3_3[2]

fRLeq:=(Rtot, Ltot, K_a_A, K_a_B) --> eq3_2[2]
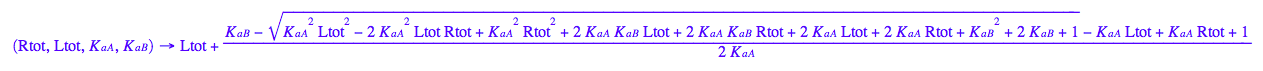
fRstareq:=(Rtot, Ltot, K_a_A, K_a_B) --> eq3_4[2]

5. Test if solution is meaningful
Set some realistic values for constants:
Rtotal:=1e-3:
Ltotal:=0.5e-3:
KaA:=1e6:
KaB:=1:
Test that all equilibrium concentrations are positive values:
if (fLeq(Rtotal, Ltotal, KaA, KaB)>0 and
fReq(Rtotal, Ltotal, KaA, KaB)>0 and
fRLeq(Rtotal, Ltotal, KaA, KaB)>0 and
fRstareq(Rtotal, Ltotal, KaA, KaB)>0
)
then
print(Unquoted,"Solution is meaningful.");
else
print(Unquoted,"WARNING!!!! Solution is NOT meaningful: some concentrations become negative!");
end_if
Solution is meaningful.
6. Check whether the solution satisfies all initial equation and conditions
Here are all original independent
equations to substitute into:
eq2_1; eq2_2; eq2_3; eq2_4
![]()
![]()
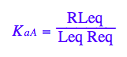
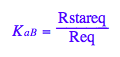
My solutions
eq3_1; eq3_2; eq3_3; eq3_4
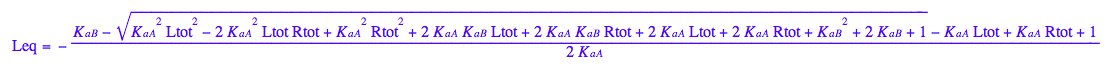
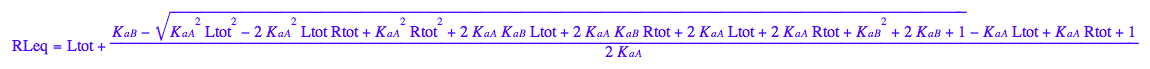


eq2_1;
% | eq3_2 | eq3_3 | eq3_4;
normal(%);
bool(%)
![]()

![]()
![]()
eq2_2;
% | eq3_1 | eq3_2;
normal(%);
bool(%)
![]()
![]()
![]()
![]()
eq2_3;
% | eq3_1 | eq3_2 | eq3_3;
normal(%);
bool(%)
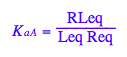
![]()
![]()
![]()
eq2_4;
% | eq3_3 | eq3_4;
normal(%);
bool(%)
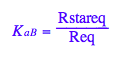
![]()
![]()
![]()
My solutions satisfy all initial equations!
7. Save results on disk for future use
(you can retrieve them later by executing: fread(filename,Quiet))
Equations we want to save:
eq3_1
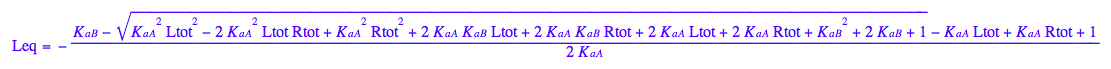
eq2_7;eq3_2
![]()
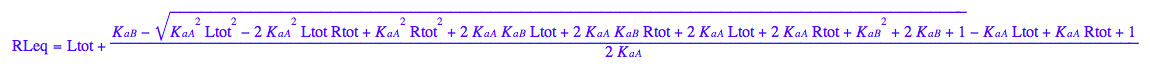
eq2_6; eq3_3
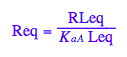

eq2_5; eq3_4
![]()

Rename them with a unique identifier of the project:
ProjectName
![]()
Leq_U_R:= eq3_1:
RLeq_U_R_short:= eq2_7:
RLeq_U_R_long:= eq3_2:
Req_U_R_short:= eq2_6:
Req_U_R_long:= eq3_3:
Rstareq_U_R_short:= eq2_5:
Rstareq_U_R_long:= eq3_4:
filename:=CurrentPath.ProjectName.".derivations";
write(filename,Leq_U_R,RLeq_U_R_short,RLeq_U_R_long,Req_U_R_short,Req_U_R_long,Rstareq_U_R_short,Rstareq_U_R_long)
![]()
Rtotal:=1e-3:
Ltotal:=0.5e-3:
KaA:=1e6:
KaB:=2:
pLeq:= plot::Function2d(
Function=(fLeq(Rtotal, L, KaA, KaB)),
LegendText="[L]",
Color = RGB::Black,
XMin=(0),
XMax=(2e-3),
XName=(L),
TitlePositionX=(0)):
pReq:= plot::Function2d(
Function=(fReq(Rtotal, L, KaA, KaB)),
LegendText="[R]",
Color = RGB::Red,
XMin=(0),
XMax=(2e-3),
XName=(L),
TitlePositionX=(0)):
pRLeq:= plot::Function2d(
Function=(fRLeq(Rtotal, L, KaA, KaB)),
LegendText="[RL]",
Color = RGB::Blue,
XMin=(0),
XMax=(2e-3),
XName=(L),
TitlePositionX=(0)):
pRstareq:= plot::Function2d(
Function=(fRstareq(Rtotal, L, KaA, KaB)),
LegendText="[R*]",
Color = RGB::Green,
XMin=(0),
XMax=(2e-3),
XName=(L),
TitlePositionX=(0)):
plot(pLeq,pReq,pRLeq,pRstareq, YAxisTitle="conc",
Height=180, Width=160,TicksLabelFont=["Helvetica",12,[0,0,0],Left], AxesTitleFont=["Helvetica",14,[0,0,0],Left], XGridVisible=TRUE, YGridVisible=TRUE,LegendVisible=TRUE, LegendFont=["Helvetica",14,[0,0,0],Left]);
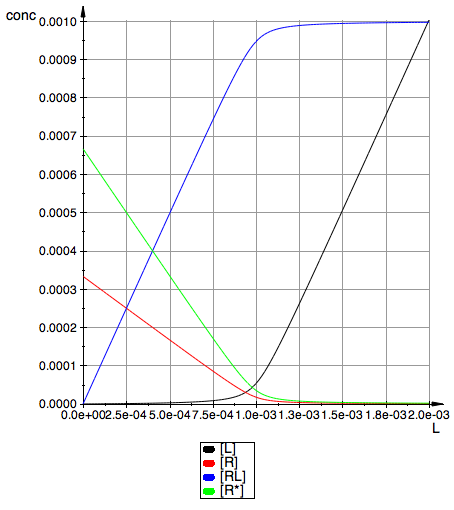
Test limiting concentrations
check R+R* total at 0
x1:=limit(fReq(Rtotal, x, KaA, KaB), x=0,Right);
x2:=limit(fRstareq(Rtotal, x, KaA, KaB), x=0,Right);
Rtotal=x1+x2;
![]()
![]()
![]()
check LR total at +INF
x1:=limit(fRLeq(Rtotal, x, KaA, KaB), x=infinity);
Rtotal=x1
![]()
![]()
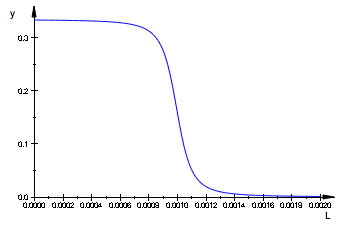
Plot differential (simulated normalized ITC curve - a sum of differentials of all components, not counting R):
df:=L -> diff(fRLeq(Rtotal, L, KaA, KaB),L) +
diff(fRstareq(Rtotal, L, KaA, KaB),L) :
plot(df(L),L=0..Rtotal*2);
1. I successfully derived analytical equations for the U-R model