ProjectName:="LRIM_U_R2L2";
CurrentPath:="/Users/kovrigin/Documents/Workspace/Data/Data.XV/EKM16.Analysis_of_multistep_kinetic_mechanisms/Equilibria/";
![]()
![]()
Analysis of U-R2L2 model
A: R + L <=> RL
B: RL <=> (RL)2
U-R2L2 is a model with a receptor dimerizes via ligand interactions (receptor lacks ability to dimerize in the absence of a ligand) and binding affinity to ligand in this quaternary complex becomes very high.
2. Derivation of working equation
3. Express concentrations of equilibrium species in terms of a found solution
4. Define functions for equilibrium concentrations
5. Test if solution is meaningful
6. Check whether the solution satisfies all initial equation and conditions
7. Save results on disk for future use
In this notebook I will write out equations for equilibrium concentrations and either solve them or generate expressions for numeric solutions for a number of models derived in /Users/kovrigin/Documents/Workspace/Data/Data.XV/EKM16.Analysis_of_multistep_kinetic_mechanisms/LRIM/Specific_models/Models.pdf
clean up workspace
reset()
Set path to save results into:
ProjectName:="LRIM_U_R2L2";
CurrentPath:="/Users/kovrigin/Documents/Workspace/Data/Data.XV/EKM16.Analysis_of_multistep_kinetic_mechanisms/Equilibria/";
![]()
![]()
Binding constants:
All binding constants I am using are formation constants so I denote them all as Ka and add a label for the transition.
K_a_A
K_a_A;
assume(K_a_A >= 0):
assumeAlso(K_a_A, R_):
![]()
K_a_B
K_a_B;
assumeAlso(K_a_B>=0):
assumeAlso(K_a_B,R_):
![]()
Total concentrations
Rtot - total concentration of the receptor
Rtot;
assumeAlso(Rtot>=0):
assumeAlso(Rtot,R_):
![]()
Ltot - total concentration of a ligand
Ltot;
assumeAlso(Ltot>=0):
assumeAlso(Ltot,R_):
![]()
Common equilibrium concentrations
Req - equilibrium concentration of a receptor monomer
Req;
assumeAlso(Req>=0):
assumeAlso(Req<=Rtot):
assumeAlso(Req,R_):
![]()
Leq - equilibrium concentration of a receptor monomer
Leq;
assumeAlso(Leq>=0):
assumeAlso(Leq<=Ltot):
assumeAlso(Leq,R_):
![]()
RLeq - equilibrium concentration of a receptor monomer
RLeq;
assumeAlso(RLeq>=0):
assumeAlso(RLeq<=Rtot):
assumeAlso(RLeq,R_):
![]()
Other species will be defined in the sections of specific models.
anames(All,User);
anames(Properties,User);

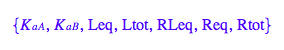
2. Derivation of working equation
Working equation: I will try to express analytical [L] from equation for a total concentration of a receptor or use it for numeric solution if analytical is not possible
[(RL)2] - equilibrium concentration of a receptor-ligand complex dimer
R2L2eq;
assumeAlso(R2L2eq>=0):
assumeAlso(R2L2eq<=Rtot):
assumeAlso(R2L2eq,R_):
![]()
Total concentrations of protein and a ligand
eq2_1:= Rtot = Req + 2*R2L2eq + RLeq;
eq2_2:= Ltot = Leq + RLeq + 2*R2L2eq;
![]()
![]()
Transition A: Equilibrium constant of ligand binding
eq2_3:= K_a_A = RLeq / (Req*Leq);
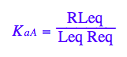
Transition B: Equilibrium constant of isomerization
eq2_4:= K_a_B = R2L2eq/RLeq^2;
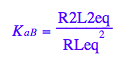
Let's get rid of [R2L2]
solve(eq2_4,R2L2eq);
eq2_5:= R2L2eq = %[1]
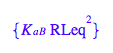
![]()
Let's get rid of [R]
solve(eq2_3,Req);
eq2_6:= Req = %[2][1]
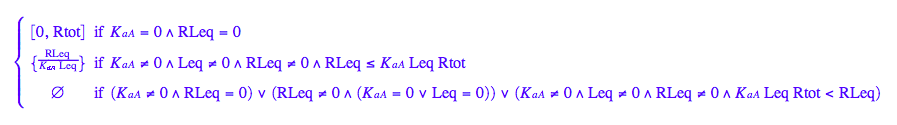
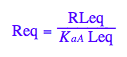
Let's get rid of [RL]
(choose one solution)
eq2_2;
% | eq2_5;
solve(%,RLeq) assuming K_a_B>0;
eq2_7:= RLeq = %[3][1]
![]()
![]()


Substitute
eq2_1;
% | eq2_5;
% | eq2_6;
% | eq2_7;
eq2_8:= %;
![]()
![]()



Final equation for [L] in terms of all constants
eq2_8

For the sake of my speed - use numerical solutions leaving analytical for future analysis.
Solve it for [L]
solutions2:=solve(eq2_8, Leq)
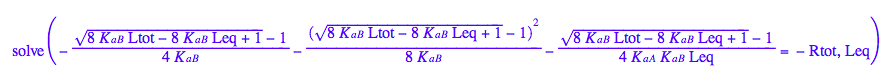
Analytically insoluble: go to Matlab
Summary of equations for equilibrium concentrations:
eq2_8

eq2_7;

eq2_6;
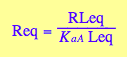
eq2_5;
![]()
1. I successfully derived equation for numeric analysis
2. System is analytically insoluble