U-2R-RL
Derivation of equilibrium thermodynamic equations for U-2R-RL system: isomerization in the binding-incompetent state of the receptor (many states) and in the bound state (induced fit)
Here I will analyze numeric solutions from "derivation.mn" document.
Clean up
reset()
Path to previous results
ProjectName:="U-2R-RL";
CurrentPath:="/Users/kovrigin_laptop/Documents/Workspace/Global_Analysis/IDAP/Mathematical_models/Equilibrium_thermodynamic_models/U-multi-path-models/nR/U-2R-RL";
![]()

Read results of derivations
filename:=CurrentPath."/".ProjectName.".mb";
fread(filename,Quiet):
anames(User)


Assume some values for testing operation
Total_R:=1e-3:
Total_L:=10e-3:
Ka:=1e3:
Kb1_s1:=2:
Kb1_s2:=3:
Kb2:=4:
test operation of all functions
fLeq_U_2R_RL(Total_R, Total_L, Ka, Kb1_s1, Kb1_s2, Kb2);
fReq_U_2R_RL(Total_R, Total_L, Ka, Kb1_s1, Kb1_s2, Kb2);
fR_s_1eq_U_2R_RL(Total_R, Total_L, Ka, Kb1_s1, Kb1_s2, Kb2);
fR_s_2eq_U_2R_RL(Total_R, Total_L, Ka, Kb1_s1, Kb1_s2, Kb2);
fRLeq_U_2R_RL(Total_R, Total_L, Ka, Kb1_s1, Kb1_s2, Kb2);
fR_sLeq_U_2R_RL(Total_R, Total_L, Ka, Kb1_s1, Kb1_s2, Kb2);
![]()
![]()
![]()
![]()
![]()
![]()
=> operative
Make wrapper functions for plotting using L/R as X axis
fLeq:=LRratio -> fLeq_U_2R_RL (Total_R, LRratio*Total_R, Ka, Kb1_s1, Kb1_s2, Kb2):
fReq:=LRratio -> fReq_U_2R_RL (Total_R, LRratio*Total_R, Ka, Kb1_s1, Kb1_s2, Kb2):
fR_s_1eq:=LRratio -> fR_s_1eq_U_2R_RL (Total_R, LRratio*Total_R, Ka, Kb1_s1, Kb1_s2, Kb2):
fR_s_2eq:=LRratio -> fR_s_2eq_U_2R_RL (Total_R, LRratio*Total_R, Ka, Kb1_s1, Kb1_s2, Kb2):
fRLeq:=LRratio -> fRLeq_U_2R_RL (Total_R, LRratio*Total_R, Ka, Kb1_s1, Kb1_s2, Kb2):
fR_sLeq:=LRratio -> fR_sLeq_U_2R_RL (Total_R, LRratio*Total_R, Ka, Kb1_s1, Kb1_s2, Kb2):
Test plotting
Total_R:=1e-3:
LRratio_max:=2:
Ka:=1e5:
Kb1_s1:=2:
Kb1_s2:=3:
Kb2:=4:
LineW:=1.5: //line width
// create plots
pLeq:= plot::Function2d(
Function=(fLeq),
LegendText="[L]",
Color = RGB::Blue,
XMin=(0),
XMax=(LRratio_max),
XName=(LRratio),
TitlePositionX=(0),
LineWidth=LineW):
pRLeq:= plot::Function2d(
Function=(fRLeq),
LegendText="[RL]",
Color = RGB::Red,
XMin=(0),
XMax=(LRratio_max),
XName=(LRratio),
TitlePositionX=(0),
LineWidth=LineW):
plot(pLeq, pRLeq, LegendVisible=TRUE)
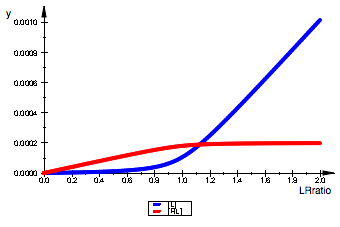
=> works
Assume some constants and evaluate titrations.
NOTE: Adjust dependent constant calculation if necessary.
Simulation_name:= "Full model":
Total_R:=1e-3:
LRratio_max:=2:
Ka:=1e5:
Kb1_s1:=2:
Kb1_s2:=4:
Kb2:=2:
LRratio_max:=1.5: // plotting range
LineW:=1.5: // plot line width
pLeq:= plot::Function2d(
Function=(fLeq),
LegendText="[L]",
Color = RGB::Blue,
XMin=(LRratio_max*1e-6),
XMax=(LRratio_max),
XName=(LRratio),
TitlePositionX=(0),
LineWidth=LineW):
pReq:= plot::Function2d(
Function=(fReq),
LegendText="[R]",
Color = RGB::Black,
XMin=(LRratio_max*1e-6),
XMax=(LRratio_max),
XName=(LRratio),
TitlePositionX=(0),
LineWidth=LineW):
pR_s_1eq:= plot::Function2d(
Function=(fR_s_1eq),
LegendText="[R*]",
Color = RGB::Green,
XMin=(LRratio_max*1e-6),
XMax=(LRratio_max),
XName=(LRratio),
TitlePositionX=(0),
LineWidth=LineW):
pR_s_2eq:= plot::Function2d(
Function=(fR_s_2eq),
LegendText="[R**]",
Color = RGB::Grey,
XMin=(LRratio_max*1e-6),
XMax=(LRratio_max),
XName=(LRratio),
TitlePositionX=(0),
LineWidth=LineW):
pRLeq:= plot::Function2d(
Function=(fRLeq),
LegendText="[RL]",
Color = RGB::Red,
XMin=(LRratio_max*1e-6),
XMax=(LRratio_max),
XName=(LRratio),
TitlePositionX=(0),
LineWidth=LineW):
pR_sLeq:= plot::Function2d(
Function=(fR_sLeq),
LegendText="[R*L]",
Color = RGB::Cyan,
XMin=(LRratio_max*1e-6),
XMax=(LRratio_max),
XName=(LRratio),
TitlePositionX=(0),
LineWidth=LineW):
// Text report
print(Unquoted, Simulation_name);
print(Unquoted, "-------------");
print(Unquoted,"Model: ".ProjectName);
print(Unquoted,"Total_R=".Total_R);
Kda:=1/Ka:
print(Unquoted,"Ka=".Ka.", Kd=".Kda);
print(Unquoted,"Kb1*=".Kb1_s1);
print(Unquoted,"Kb1**=".Kb1_s2);
Kc21:=Kb1_s2/Kb1_s1:
print(Unquoted,"Kc*-**=".Kc21);
print(Unquoted,"Kb2=".Kb2);
// plot all together
plot(pLeq, pReq, pR_s_1eq, pR_s_2eq, pRLeq, pR_sLeq,
YAxisTitle="[X]", Header=("Model: ".ProjectName),
Height=160, Width=100,TicksLabelFont=["Helvetica",12,[0,0,0],Left],
AxesTitleFont=["Helvetica",14,[0,0,0],Left],
XGridVisible=TRUE, YGridVisible=TRUE,
LegendVisible=TRUE, LegendFont=["Helvetica",14,[0,0,0],Left],
ViewingBoxYMax=Total_R);
Full model
-------------
Model: U-2R-RL
Total_R=0.001
Ka=100000.0, Kd=0.00001
Kb1*=2
Kb1**=4
Kc*-**=2
Kb2=2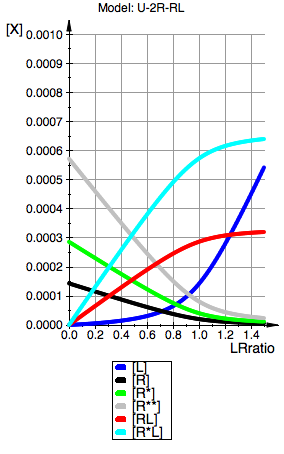
Jump back to the beginning of simulation section
Jump back to the beginning of simulation section
Test of the model: titration of R with L
|
Reduce to U |
Reduce to U-RL |
Reduce to U-R (use R*) |
Reduce to U-R (use R**) |
|
Full model |
|
|
|
|
|
|
|
|
|
|
|
|
|
Conclusion:
The model works as expected