5U-R-RL
Derivation of differential equations and kinetic matrices describing evolution of spin concentrations

NOTE: This document is based on IDAP/Mathematical_models/Equilibrium_thermodynamic_models/U-multi-path-models/nU/5U-R-RL
NOTE 2: The model with one isomerization, 1U-R-RL, is not identical to U-R-RL because the latter contains a transition connecting R* and RL* directly, which is absent from nU-R-RL family models! It, however , is identical to U-1R-RL from U-nR-RL family (with different order of the species).
Strategy:
I will develop kinetic matrices for five cases to have from one to five isomers of R. I will explicitly use all rate constants of similar transitions to be able to simplify in the next steps by setting them to one value. The thermodynamic model includes 5-isomers and was designed to be reducible by appropriate settings of the equilibrium constants.
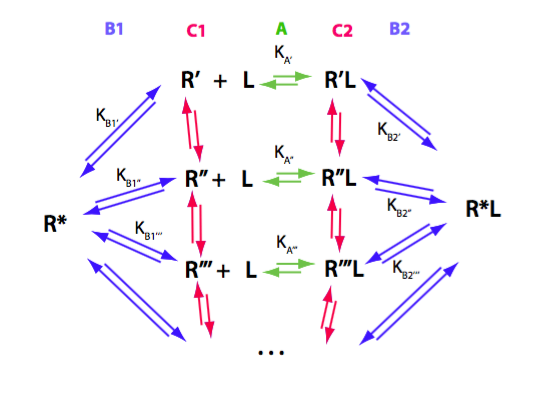
Order of species to allow for easy expansion of matrices:
R*, RL*, R', RL', R'', RL'', R''', RL''', R'''', RL'''', R''''', RL'''''
Accurate extraction of K matrix:
Workflow for accurate extraction of the K matrix
- prepare empty matrix
- copy-paste one equation at a time to MATLAB script
- in MATLAB: arrange terms with increasing coefficients, place commas after groups with the same coefficient , insert zeros for the absent coefficients
- cut-and-paste entire line into the MuPad.
- execute cell after every equation to see how matrix is filled
- delete coefficients (keep negative signs!!!)
- check rules along the column and the row
Definitions of transitions and strategy
Reaction, partial conversion, and net rates
Expression in terms of spin (monomer) concentrations
Control derivation of 1U-R-RL mechanism with conventional order of species
Expession of K matrix for 1U-R-RL mechanism with current order of species
K matrix for 1U-R-RL model with new species order
Expession of K matrix for 2U-R-RL mechanism
Expession of K matrix for 3U-R-RL mechanism
Expession of K matrix for 4U-R-RL mechanism
Expession of K matrix for 5U-R-RL mechanism
clean up workspace
reset()
Definition of transitions and strategy
Write properly balanced reactions equations for all transitions in the mechanism:
Binding reaction, transitions A:
R'+L<=>RL'
Constants: k_1_A_p_1 (forward), k_2_A_p_1 (reverse).
R''+L<=>RL''
Constants: k_1_A_p_2 (forward), k_2_A_p_2 (reverse).
R'''+L<=>RL'''
Constants: k_1_A_p_3 (forward), k_2_A_p_3 (reverse).
R''''+L<=>RL''''
Constants: k_1_A_p_4 (forward), k_2_A_p_4 (reverse).
R'''''+L<=>RL'''''
Constants: k_1_A_p_5 (forward), k_2_A_p_5 (reverse).
Isomerization of R' to R* species: transitions B1
R* <=> R'
Constants: k_1_B_1_p_1 (forward), k_2_B_1_p_1 (reverse).
R* <=> R''
Constants: k_1_B_1_p_2 (forward), k_2_B_1_p_2 (reverse).
R* <=> R'''
Constants: k_1_B_1_p_3 (forward), k_2_B_1_p_3 (reverse).
R* <=> R''''
Constants: k_1_B_1_p_4 (forward), k_2_B_1_p_4 (reverse).
R* <=> R'''''
Constants: k_1_B_1_p_5 (forward), k_2_B_1_p_5 (reverse).
Isomerization of RL-primed to RL* species: transition B2
RL' <=> R*L
Constants: k_1_B_2_p_1 (forward), k_2_B_2_p_1 (reverse).
RL'' <=> R*L
Constants: k_1_B_2_p_2 (forward), k_2_B_2_p_2 (reverse).
RL'''<=> R*L
Constants: k_1_B_2_p_3 (forward), k_2_B_2_p_3 (reverse).
RL'''' <=> R*L
Constants: k_1_B_2_p_4 (forward), k_2_B_2_p_4 (reverse).
RL''''' <=> R*L
Constants: k_1_B_2_p_5 (forward), k_2_B_2_p_5 (reverse).
Interconversion of R-primed isomers: transitions C1
-- R' --
R' <=> R''
Constants: k_1_C_1_p_1_2 (forward), k_2_C_1_p_1_2 (reverse).
R' <=> R'''
Constants: k_1_C_1_p_1_3 (forward), k_2_C_1_p_1_3 (reverse).
R' <=> R''''
Constants: k_1_C_1_p_1_4 (forward), k_2_C_1_p_1_4 (reverse).
R' <=> R'''''
Constants: k_1_C_1_p_1_5 (forward), k_2_C_1_p_1_5 (reverse).
-- R'' --
R'' <=> R'''
Constants: k_1_C_1_p_2_3 (forward), k_2_C_1_p_2_3 (reverse).
R'' <=> R''''
Constants: k_1_C_1_p_2_4 (forward), k_2_C_1_p_2_4 (reverse).
R'' <=> R'''''
Constants: k_1_C_1_p_2_5 (forward), k_2_C_1_p_2_5 (reverse).
-- R''' --
R''' <=> R''''
Constants: k_1_C_1_p_3_4 (forward), k_2_C_1_p_3_4 (reverse).
R''' <=> R'''''
Constants: k_1_C_1_p_3_5 (forward), k_2_C_1_p_3_5 (reverse).
-- R'''' --
R'''' <=> R'''''
Constants: k_1_C_1_p_4_5 (forward), k_2_C_1_p_4_5 (reverse).
Interconversion of RL-primed isomers: transitions C2
-- RL' --
RL' <=> RL''
Constants: k_1_C_2_p_1_2 (forward), k_2_C_2_p_1_2 (reverse).
RL' <=> RL'''
Constants: k_1_C_2_p_1_3 (forward), k_2_C_2_p_1_3 (reverse).
RL' <=> RL''''
Constants: k_1_C_2_p_1_4 (forward), k_2_C_2_p_1_4 (reverse).
RL' <=> RL'''''
Constants: k_1_C_2_p_1_5 (forward), k_2_C_2_p_1_5 (reverse).
-- RL'' --
RL'' <=> RL'''
Constants: k_1_C_2_p_2_3 (forward), k_2_C_2_p_2_3 (reverse).
RL'' <=> RL''''
Constants: k_1_C_2_p_2_4 (forward), k_2_C_2_p_2_4 (reverse).
RL'' <=> RL'''''
Constants: k_1_C_2_p_2_5 (forward), k_2_C_2_p_2_5 (reverse).
-- RL''' --
RL''' <=> RL''''
Constants: k_1_C_2_p_3_4 (forward), k_2_C_2_p_3_4 (reverse).
RL''' <=> RL'''''
Constants: k_1_C_2_p_3_5 (forward), k_2_C_2_p_3_5 (reverse).
-- RL'''' --
RL'''' <=> RL'''''
Constants: k_1_C_2_p_4_5 (forward), k_2_C_2_p_4_5 (reverse).
WORKING NOTE: Species completed and not completed yet: R*, RL*, R', RL', R'', RL'', R''', RL''', R'''', RL'''', R''''', RL'''''
Contents
- Summary equations for R'''''
- Summary of equations for RL''
- Summary of equations for RL'''
- Summary of equations for RL''''
- Summary of equations for RL'''''
- Summary of equations for RL*
Write reaction rates
Here, we distinguish reaction rate (elementary reaction acts per unit time; denote as "Rate_reaction-label") and conversion rates (number of moles of specific species consumed/produced per unit time, dc/dt). Conversion rates, dc/dt, for species are related to reaction rates, Rate, through molecularity coefficients.
We also distinguish here partial conversion rates from net (overall) conversion rates. The net conversion rate is the actual rate of change in measured concentration of the species due to all transitions this species is involved with (denote at Rate_reaction-label_N). Partial conversion rate is the conversion rate of the species along a specific branch of the reaction mechanism (denote 'dC-component-dt-reaction-label'). Summation of the partial conversion rates of the species gives the net conversion rate.
NOTE: In this mechanism, all transition involve only one molecules of species of each kind, therefore all partial conversion rates are equal to reaction rates. This is reflected by setting 'molecularity' to 1 for all transitions. The molecularity sign also indicates whether the species is created or destroyed in this transition.
Strategy:
We need equations for the net conversion rates for each species. For this purpose, we write partial conversion rates originating from every individual (forward or reverse) process. To obtain the partial conversion rate for a process, we use the reaction rate equation times molecularity of the process in terms of this particular species.
1. Each species is analyzed in a separate "Equations group".
3. In each subgroup, equations have uniform numbering system. Yet, beware of cut-and-paste errors!
4. Inside each subgroup, first three equations are to account for FORWARD process. The second three are for REVERSE. It is
reliable to write the first three from scratch and then copy-paste with necessary modifications to make last three.
in Definitions of transitions and strategy
Equations group: Rp1
R'+L<=>RL'
Constants: k_1_A_p_1 (forward), k_2_A_p_1 (reverse).
Equations subgroup: Ap1
a forward reaction rate
eq_Rp1_Ap1_1a:= Rate_1_A_p_1 = k_1_A_p_1*R_p_1*L
![]()
a partial conversion rate of R' in this transition
molecularity:=-1:
eq_Rp1_Ap1_1b:= dcRp1dt_1_A_p_1 = molecularity*Rate_1_A_p_1
![]()
The final form
eq_Rp1_Ap1_1c:= eq_Rp1_Ap1_1b | eq_Rp1_Ap1_1a
![]()
a reverse reaction rate for the transition
eq_Rp1_Ap1_2a:= Rate_2_A_p_1 = k_2_A_p_1*RL_p_1
![]()
a partial conversion rate of R in this transition
molecularity:=1:
eq_Rp1_Ap1_2b:= dcRp1dt_2_A_p_1 = molecularity*Rate_2_A_p_1
![]()
The final form
eq_Rp1_Ap1_2c:= eq_Rp1_Ap1_2b | eq_Rp1_Ap1_2a
![]()
R* <=> R'
Constants: k_1_B_1_p_1 (forward), k_2_B_1_p_1 (reverse).
Equations subgroup: B1p1
a forward reaction rate for the transition
eq_Rp1_B1p1_1a:= Rate_1_B_1_p_1 = k_1_B_1_p_1*R_s
![]()
a partial conversion rate of R' in this transition
molecularity:=1:
eq_Rp1_B1p1_1b:= dcRp1dt_1_B_1_p_1 = molecularity*Rate_1_B_1_p_1
![]()
The final form
eq_Rp1_B1p1_1c:= eq_Rp1_B1p1_1b | eq_Rp1_B1p1_1a
![]()
a reverse reaction rate for the transition
eq_Rp1_B1p1_2a:= Rate_2_B_1_p_1 = k_2_B_1_p_1*R_p_1
![]()
a partial conversion rate of R' in this transition
molecularity:=-1:
eq_Rp1_B1p1_2b:= dcRp1dt_2_B_1_p_1 = molecularity*Rate_2_B_1_p_1
![]()
The final form
eq_Rp1_B1p1_2c:= eq_Rp1_B1p1_2b | eq_Rp1_B1p1_2a
![]()
R' <=> R''
Constants: k_1_C_1_p_1_2 (forward), k_2_C_1_p_1_2 (reverse).
Equations subgroup: C1p12
a forward reaction rate for the transition
eq_Rp1_C1p12_1a:= Rate_1_C_1_p_1_2 = k_1_C_1_p_1_2*R_p_1
![]()
a partial conversion rate of R' in this transition
molecularity:=-1:
eq_Rp1_C1p12_1b:= dcRp1dt_1_C_1_p_1_2 = molecularity*Rate_1_C_1_p_1_2
![]()
The final form
eq_Rp1_C1p12_1c:= eq_Rp1_C1p12_1b | eq_Rp1_C1p12_1a
![]()
a reverse reaction rate for the transition
eq_Rp1_C1p12_2a:= Rate_2_C_1_p_1_2 = k_2_C_1_p_1_2*R_p_2
![]()
a partial conversion rate of R' in this transition
molecularity:=1:
eq_Rp1_C1p12_2b:= dcRp1dt_2_C_1_p_1_2 = molecularity*Rate_2_C_1_p_1_2
![]()
The final form
eq_Rp1_C1p12_2c:= eq_Rp1_C1p12_2b | eq_Rp1_C1p12_2a
![]()
R' <=> R'''
Constants: k_1_C_1_p_1_3 (forward), k_2_C_1_p_1_3 (reverse).
Equations subgroup: C1p13
a forward reaction rate for the transition
eq_Rp1_C1p13_1a:= Rate_1_C_1_p_1_3 = k_1_C_1_p_1_3*R_p_1
![]()
a partial conversion rate of R' in this transition
molecularity:=-1:
eq_Rp1_C1p13_1b:= dcRp1dt_1_C_1_p_1_3 = molecularity*Rate_1_C_1_p_1_3
![]()
The final form
eq_Rp1_C1p13_1c:= eq_Rp1_C1p13_1b | eq_Rp1_C1p13_1a
![]()
a reverse reaction rate for the transition
eq_Rp1_C1p13_2a:= Rate_2_C_1_p_1_3 = k_2_C_1_p_1_3*R_p_3
![]()
a partial conversion rate of R' in this transition
molecularity:=1:
eq_Rp1_C1p13_2b:= dcRp1dt_2_C_1_p_1_3 = molecularity*Rate_2_C_1_p_1_3
![]()
The final form
eq_Rp1_C1p13_2c:= eq_Rp1_C1p13_2b | eq_Rp1_C1p13_2a
![]()
R' <=> R''''
Constants: k_1_C_1_p_1_4 (forward), k_2_C_1_p_1_4 (reverse).
Equations subgroup: C1p14
a forward reaction rate for the transition
eq_Rp1_C1p14_1a:= Rate_1_C_1_p_1_4 = k_1_C_1_p_1_4*R_p_1
![]()
a partial conversion rate of R' in this transition
molecularity:=-1:
eq_Rp1_C1p14_1b:= dcRp1dt_1_C_1_p_1_4 = molecularity*Rate_1_C_1_p_1_4
![]()
The final form
eq_Rp1_C1p14_1c:= eq_Rp1_C1p14_1b | eq_Rp1_C1p14_1a
![]()
a reverse reaction rate for the transition
eq_Rp1_C1p14_2a:= Rate_2_C_1_p_1_4 = k_2_C_1_p_1_4*R_p_4
![]()
a partial conversion rate of R' in this transition
molecularity:=1:
eq_Rp1_C1p14_2b:= dcRp1dt_2_C_1_p_1_4 = molecularity*Rate_2_C_1_p_1_4
![]()
The final form
eq_Rp1_C1p14_2c:= eq_Rp1_C1p14_2b | eq_Rp1_C1p14_2a
![]()
R' <=> R'''''
Constants: k_1_C_1_p_1_5 (forward), k_2_C_1_p_1_5 (reverse).
Equations subgroup: C1p15
a forward reaction rate for the transition
eq_Rp1_C1p15_1a:= Rate_1_C_1_p_1_5 = k_1_C_1_p_1_5*R_p_1
![]()
a partial conversion rate of R' in this transition
molecularity:=-1:
eq_Rp1_C1p15_1b:= dcRp1dt_1_C_1_p_1_5 = molecularity*Rate_1_C_1_p_1_5
![]()
The final form
eq_Rp1_C1p15_1c:= eq_Rp1_C1p15_1b | eq_Rp1_C1p15_1a
![]()
a reverse reaction rate for the transition
eq_Rp1_C1p15_2a:= Rate_2_C_1_p_1_5 = k_2_C_1_p_1_5*R_p_5
![]()
a partial conversion rate of R' in this transition
molecularity:=1:
eq_Rp1_C1p15_2b:= dcRp1dt_2_C_1_p_1_5 = molecularity*Rate_2_C_1_p_1_5
![]()
The final form
eq_Rp1_C1p15_2c:= eq_Rp1_C1p15_2b | eq_Rp1_C1p15_2a
![]()
Summary of partial conversion rates for the species
eq_Rp1_Ap1_1c;eq_Rp1_Ap1_2c;
![]()
![]()
eq_Rp1_B1p1_1c;eq_Rp1_B1p1_2c
![]()
![]()
eq_Rp1_C1p12_1c;eq_Rp1_C1p12_2c;
eq_Rp1_C1p13_1c;eq_Rp1_C1p13_2c;
eq_Rp1_C1p14_1c;eq_Rp1_C1p14_2c;
eq_Rp1_C1p15_1c;eq_Rp1_C1p15_2c;
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Net conversion rate for the species
I will create equations for all five versions of the mechanism.
1U-R-RL
dcRp1dt_N = dcRp1dt_1_A_p_1 + dcRp1dt_2_A_p_1 + dcRp1dt_1_B_1_p_1 + dcRp1dt_2_B_1_p_1
![]()
Substitute (use all equations)
eq_Rp1_N__1U_R_RL:= % | eq_Rp1_Ap1_1c | eq_Rp1_Ap1_2c \
| eq_Rp1_B1p1_1c | eq_Rp1_B1p1_2c \
| eq_Rp1_C1p12_1c | eq_Rp1_C1p12_2c \
| eq_Rp1_C1p13_1c | eq_Rp1_C1p13_2c \
| eq_Rp1_C1p14_1c | eq_Rp1_C1p14_2c \
| eq_Rp1_C1p15_1c | eq_Rp1_C1p15_2c;
![]()
2U-R-RL
dcRp1dt_N = dcRp1dt_1_A_p_1 + dcRp1dt_2_A_p_1 + dcRp1dt_1_B_1_p_1 + dcRp1dt_2_B_1_p_1 +\
dcRp1dt_1_C_1_p_1_2 + dcRp1dt_2_C_1_p_1_2;
![]()
Substitute (use all equations)
eq_Rp1_N__2U_R_RL:= % | eq_Rp1_Ap1_1c | eq_Rp1_Ap1_2c \
| eq_Rp1_B1p1_1c | eq_Rp1_B1p1_2c \
| eq_Rp1_C1p12_1c | eq_Rp1_C1p12_2c \
| eq_Rp1_C1p13_1c | eq_Rp1_C1p13_2c \
| eq_Rp1_C1p14_1c | eq_Rp1_C1p14_2c \
| eq_Rp1_C1p15_1c | eq_Rp1_C1p15_2c;
![]()
3U-R-RL
dcRp1dt_N = dcRp1dt_1_A_p_1 + dcRp1dt_2_A_p_1 + dcRp1dt_1_B_1_p_1 + dcRp1dt_2_B_1_p_1 +\
dcRp1dt_1_C_1_p_1_2 + dcRp1dt_2_C_1_p_1_2 + \
dcRp1dt_1_C_1_p_1_3 + dcRp1dt_2_C_1_p_1_3;
![]()
Substitute (use all equations)
eq_Rp1_N__3U_R_RL:= % | eq_Rp1_Ap1_1c | eq_Rp1_Ap1_2c \
| eq_Rp1_B1p1_1c | eq_Rp1_B1p1_2c \
| eq_Rp1_C1p12_1c | eq_Rp1_C1p12_2c \
| eq_Rp1_C1p13_1c | eq_Rp1_C1p13_2c \
| eq_Rp1_C1p14_1c | eq_Rp1_C1p14_2c \
| eq_Rp1_C1p15_1c | eq_Rp1_C1p15_2c;
![]()
4U-R-RL
dcRp1dt_N = dcRp1dt_1_A_p_1 + dcRp1dt_2_A_p_1 + dcRp1dt_1_B_1_p_1 + dcRp1dt_2_B_1_p_1 +\
dcRp1dt_1_C_1_p_1_2 + dcRp1dt_2_C_1_p_1_2 + \
dcRp1dt_1_C_1_p_1_3 + dcRp1dt_2_C_1_p_1_3 + \
dcRp1dt_1_C_1_p_1_4 + dcRp1dt_2_C_1_p_1_4;

Substitute (use all equations)
eq_Rp1_N__4U_R_RL:= % | eq_Rp1_Ap1_1c | eq_Rp1_Ap1_2c \
| eq_Rp1_B1p1_1c | eq_Rp1_B1p1_2c \
| eq_Rp1_C1p12_1c | eq_Rp1_C1p12_2c \
| eq_Rp1_C1p13_1c | eq_Rp1_C1p13_2c \
| eq_Rp1_C1p14_1c | eq_Rp1_C1p14_2c \
| eq_Rp1_C1p15_1c | eq_Rp1_C1p15_2c;
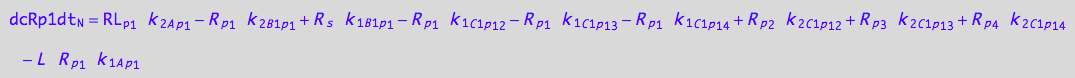
5U-R-RL
dcRp1dt_N = dcRp1dt_1_A_p_1 + dcRp1dt_2_A_p_1 + dcRp1dt_1_B_1_p_1 + dcRp1dt_2_B_1_p_1 +\
dcRp1dt_1_C_1_p_1_2 + dcRp1dt_2_C_1_p_1_2 + \
dcRp1dt_1_C_1_p_1_3 + dcRp1dt_2_C_1_p_1_3 + \
dcRp1dt_1_C_1_p_1_4 + dcRp1dt_2_C_1_p_1_4 + \
dcRp1dt_1_C_1_p_1_5 + dcRp1dt_2_C_1_p_1_5;

Substitute (use all equations)
eq_Rp1_N__5U_R_RL:= % | eq_Rp1_Ap1_1c | eq_Rp1_Ap1_2c \
| eq_Rp1_B1p1_1c | eq_Rp1_B1p1_2c \
| eq_Rp1_C1p12_1c | eq_Rp1_C1p12_2c \
| eq_Rp1_C1p13_1c | eq_Rp1_C1p13_2c \
| eq_Rp1_C1p14_1c | eq_Rp1_C1p14_2c \
| eq_Rp1_C1p15_1c | eq_Rp1_C1p15_2c;

eq_Rp1_N__1U_R_RL
![]()
eq_Rp1_N__2U_R_RL
![]()
eq_Rp1_N__3U_R_RL
![]()
eq_Rp1_N__4U_R_RL
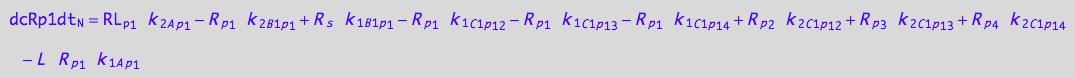
eq_Rp1_N__5U_R_RL

Back to Equations for each species
Equations group: Rp2
R''+L<=>RL''
Constants: k_1_A_p_2 (forward), k_2_A_p_2 (reverse).
Equations subgroup: Ap2
a forward reaction rate
eq_Rp2_Ap2_1a:= Rate_1_A_p_2 = k_1_A_p_2*R_p_2*L
![]()
a partial conversion rate of R'' in this transition
molecularity:=-1:
eq_Rp2_Ap2_1b:= dcRp2dt_1_A_p_2 = molecularity*Rate_1_A_p_2
![]()
The final form
eq_Rp2_Ap2_1c:= eq_Rp2_Ap2_1b | eq_Rp2_Ap2_1a
![]()
a reverse reaction rate for the transition
eq_Rp2_Ap2_2a:= Rate_2_A_p_2 = k_2_A_p_2*RL_p_2
![]()
a partial conversion rate of R'' in this transition
molecularity:=1:
eq_Rp2_Ap2_2b:= dcRp2dt_2_A_p_2 = molecularity*Rate_2_A_p_2
![]()
The final form
eq_Rp2_Ap2_2c:= eq_Rp2_Ap2_2b | eq_Rp2_Ap2_2a
![]()
R* <=> R''
Constants: k_1_B_1_p_2 (forward), k_2_B_1_p_2 (reverse).
Equations subgroup: B1p2
a forward reaction rate for the transition
eq_Rp2_B1p2_1a:= Rate_1_B_1_p_2 = k_1_B_1_p_2*R_s
![]()
a partial conversion rate of R'' in this transition
molecularity:=1:
eq_Rp2_B1p2_1b:= dcRp2dt_1_B_1_p_2 = molecularity*Rate_1_B_1_p_2
![]()
The final form
eq_Rp2_B1p2_1c:= eq_Rp2_B1p2_1b | eq_Rp2_B1p2_1a
![]()
a reverse reaction rate for the transition
eq_Rp2_B1p2_2a:= Rate_2_B_1_p_2 = k_2_B_1_p_2*R_p_2
![]()
a partial conversion rate of R'' in this transition
molecularity:=-1:
eq_Rp2_B1p2_2b:= dcRp2dt_2_B_1_p_2 = molecularity*Rate_2_B_1_p_2
![]()
The final form
eq_Rp2_B1p2_2c:= eq_Rp2_B1p2_2b | eq_Rp2_B1p2_2a
![]()
R' <=> R''
Constants: k_1_C_1_p_1_2 (forward), k_2_C_1_p_1_2 (reverse).
NOTE: Kinetic equations for this transitions were already defined!
Equations subgroup: C1p12
a forward reaction rate for the transition
eq_Rp2_C1p12_1a:= eq_Rp1_C1p12_1a
![]()
a partial conversion rate of R'' in this transition
molecularity:=1:
eq_Rp2_C1p12_1b:= dcRp2dt_1_C_1_p_1_2 = molecularity*Rate_1_C_1_p_1_2
![]()
The final form
eq_Rp2_C1p12_1c:= eq_Rp2_C1p12_1b | eq_Rp2_C1p12_1a
![]()
a reverse reaction rate for the transition
eq_Rp2_C1p12_2a:= eq_Rp1_C1p12_2a
![]()
a partial conversion rate of R'' in this transition
molecularity:=-1:
eq_Rp2_C1p12_2b:= dcRp2dt_2_C_1_p_1_2 = molecularity*Rate_2_C_1_p_1_2
![]()
The final form
eq_Rp2_C1p12_2c:= eq_Rp2_C1p12_2b | eq_Rp2_C1p12_2a
![]()
R'' <=> R'''
Constants: k_1_C_1_p_2_3 (forward), k_2_C_1_p_2_3 (reverse).
Equations subgroup: C1p23
a forward reaction rate for the transition
eq_Rp2_C1p23_1a:= Rate_1_C_1_p_2_3 = k_1_C_1_p_2_3*R_p_2
![]()
a partial conversion rate of R'' in this transition
molecularity:=-1:
eq_Rp2_C1p23_1b:= dcRp2dt_1_C_1_p_2_3 = molecularity*Rate_1_C_1_p_2_3
![]()
The final form
eq_Rp2_C1p23_1c:= eq_Rp2_C1p23_1b | eq_Rp2_C1p23_1a
![]()
a reverse reaction rate for the transition
eq_Rp2_C1p23_2a:= Rate_2_C_1_p_2_3 = k_2_C_1_p_2_3*R_p_3
![]()
a partial conversion rate of R'' in this transition
molecularity:=1:
eq_Rp2_C1p23_2b:= dcRp2dt_2_C_1_p_2_3 = molecularity*Rate_2_C_1_p_2_3
![]()
The final form
eq_Rp2_C1p23_2c:= eq_Rp2_C1p23_2b | eq_Rp2_C1p23_2a
![]()
R'' <=> R''''
Constants: k_1_C_1_p_2_4 (forward), k_2_C_1_p_2_4 (reverse).
Equations subgroup: C1p24
a forward reaction rate for the transition
eq_Rp2_C1p24_1a:= Rate_1_C_1_p_2_4 = k_1_C_1_p_2_4*R_p_2
![]()
a partial conversion rate of R'' in this transition
molecularity:=-1:
eq_Rp2_C1p24_1b:= dcRp2dt_1_C_1_p_2_4 = molecularity*Rate_1_C_1_p_2_4
![]()
The final form
eq_Rp2_C1p24_1c:= eq_Rp2_C1p24_1b | eq_Rp2_C1p24_1a
![]()
a reverse reaction rate for the transition
eq_Rp2_C1p24_2a:= Rate_2_C_1_p_2_4 = k_2_C_1_p_2_4*R_p_4
![]()
a partial conversion rate of R'' in this transition
molecularity:=1:
eq_Rp2_C1p24_2b:= dcRp2dt_2_C_1_p_2_4 = molecularity*Rate_2_C_1_p_2_4
![]()
The final form
eq_Rp2_C1p24_2c:= eq_Rp2_C1p24_2b | eq_Rp2_C1p24_2a
![]()
R'' <=> R'''''
Constants: k_1_C_1_p_2_5 (forward), k_2_C_1_p_2_5 (reverse).
Equations subgroup: C1p25
a forward reaction rate for the transition
eq_Rp2_C1p25_1a:= Rate_1_C_1_p_2_5 = k_1_C_1_p_2_5*R_p_2
![]()
a partial conversion rate of R'' in this transition
molecularity:=-1:
eq_Rp2_C1p25_1b:= dcRp2dt_1_C_1_p_2_5 = molecularity*Rate_1_C_1_p_2_5
![]()
the final form
eq_Rp2_C1p25_1c:= eq_Rp2_C1p25_1b | eq_Rp2_C1p25_1a
![]()
a reverse reaction rate for the transition
eq_Rp2_C1p25_2a:= Rate_2_C_1_p_2_5 = k_2_C_1_p_2_5*R_p_5
![]()
a partial conversion rate of R'' in this transition
molecularity:=1:
eq_Rp2_C1p25_2b:= dcRp2dt_2_C_1_p_2_5 = molecularity*Rate_2_C_1_p_2_5
![]()
The final form
eq_Rp2_C1p25_2c:= eq_Rp2_C1p25_2b | eq_Rp2_C1p25_2a
![]()
Summary of partial conversion rates for the species
eq_Rp2_Ap2_1c;eq_Rp2_Ap2_2c;
![]()
![]()
eq_Rp2_B1p2_1c;eq_Rp2_B1p2_2c
![]()
![]()
eq_Rp2_C1p12_1c;eq_Rp2_C1p12_2c;
eq_Rp2_C1p23_1c;eq_Rp2_C1p23_2c;
eq_Rp2_C1p24_1c;eq_Rp2_C1p24_2c;
eq_Rp2_C1p25_1c;eq_Rp2_C1p25_2c;
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Net conversion rate for the species
I will create equations for all five versions of the mechanism.
1U-R-RL - not needed (does not have R'' species)
2U-R-RL
dcRp2dt_N = dcRp2dt_1_A_p_2 + dcRp2dt_2_A_p_2 +\
dcRp2dt_1_B_1_p_2 + dcRp2dt_2_B_1_p_2 +\
dcRp2dt_1_C_1_p_1_2 + dcRp2dt_2_C_1_p_1_2 ;
![]()
Substitute (use all equations)
eq_Rp2_N__2U_R_RL:= % |\
eq_Rp2_Ap2_1c | eq_Rp2_Ap2_2c |\
eq_Rp2_B1p2_1c | eq_Rp2_B1p2_2c |\
eq_Rp2_C1p12_1c | eq_Rp2_C1p12_2c |\
eq_Rp2_C1p23_1c | eq_Rp2_C1p23_2c |\
eq_Rp2_C1p24_1c | eq_Rp2_C1p24_2c |\
eq_Rp2_C1p25_1c | eq_Rp2_C1p25_2c;
![]()
3U-R-RL
dcRp2dt_N = dcRp2dt_1_A_p_2 + dcRp2dt_2_A_p_2 +\
dcRp2dt_1_B_1_p_2 + dcRp2dt_2_B_1_p_2 +\
dcRp2dt_1_C_1_p_1_2 + dcRp2dt_2_C_1_p_1_2 +\
dcRp2dt_1_C_1_p_2_3 + dcRp2dt_2_C_1_p_2_3 ;
![]()
Substitute (use all equations)
eq_Rp2_N__3U_R_RL:= % |\
eq_Rp2_Ap2_1c | eq_Rp2_Ap2_2c |\
eq_Rp2_B1p2_1c | eq_Rp2_B1p2_2c |\
eq_Rp2_C1p12_1c | eq_Rp2_C1p12_2c |\
eq_Rp2_C1p23_1c | eq_Rp2_C1p23_2c |\
eq_Rp2_C1p24_1c | eq_Rp2_C1p24_2c |\
eq_Rp2_C1p25_1c | eq_Rp2_C1p25_2c;
![]()
4U-R-RL
dcRp2dt_N = dcRp2dt_1_A_p_2 + dcRp2dt_2_A_p_2 +\
dcRp2dt_1_B_1_p_2 + dcRp2dt_2_B_1_p_2 +\
dcRp2dt_1_C_1_p_1_2 + dcRp2dt_2_C_1_p_1_2 +\
dcRp2dt_1_C_1_p_2_3 + dcRp2dt_2_C_1_p_2_3 +\
dcRp2dt_1_C_1_p_2_4 + dcRp2dt_2_C_1_p_2_4 ;

Substitute (use all equations)
eq_Rp2_N__4U_R_RL:= % |\
eq_Rp2_Ap2_1c | eq_Rp2_Ap2_2c |\
eq_Rp2_B1p2_1c | eq_Rp2_B1p2_2c |\
eq_Rp2_C1p12_1c | eq_Rp2_C1p12_2c |\
eq_Rp2_C1p23_1c | eq_Rp2_C1p23_2c |\
eq_Rp2_C1p24_1c | eq_Rp2_C1p24_2c |\
eq_Rp2_C1p25_1c | eq_Rp2_C1p25_2c;
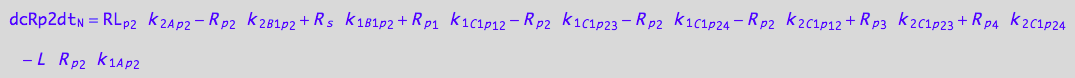
5U-R-RL
dcRp2dt_N = dcRp2dt_1_A_p_2 + dcRp2dt_2_A_p_2 +\
dcRp2dt_1_B_1_p_2 + dcRp2dt_2_B_1_p_2 +\
dcRp2dt_1_C_1_p_1_2 + dcRp2dt_2_C_1_p_1_2 +\
dcRp2dt_1_C_1_p_2_3 + dcRp2dt_2_C_1_p_2_3 +\
dcRp2dt_1_C_1_p_2_4 + dcRp2dt_2_C_1_p_2_4 +\
dcRp2dt_1_C_1_p_2_5 + dcRp2dt_2_C_1_p_2_5 ;

Substitute (use all equations)
eq_Rp2_N__5U_R_RL:= % |\
eq_Rp2_Ap2_1c | eq_Rp2_Ap2_2c |\
eq_Rp2_B1p2_1c | eq_Rp2_B1p2_2c |\
eq_Rp2_C1p12_1c | eq_Rp2_C1p12_2c |\
eq_Rp2_C1p23_1c | eq_Rp2_C1p23_2c |\
eq_Rp2_C1p24_1c | eq_Rp2_C1p24_2c |\
eq_Rp2_C1p25_1c | eq_Rp2_C1p25_2c;
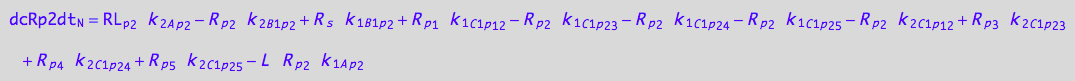
eq_Rp2_N__2U_R_RL
![]()
eq_Rp2_N__3U_R_RL
![]()
eq_Rp2_N__4U_R_RL
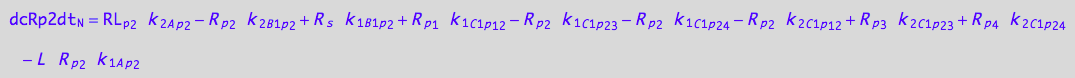
eq_Rp2_N__5U_R_RL
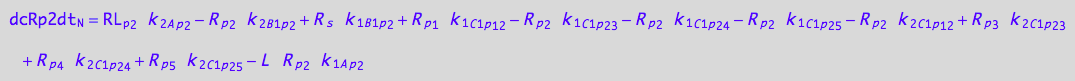
Back to Equations for each species
Equations group: Rp3
R'''+L<=>RL'''
Constants: k_1_A_p_3 (forward), k_2_A_p_3 (reverse).
Equations subgroup: Ap3
a forward reaction rate
eq_Rp3_Ap3_1a:= Rate_1_A_p_3 = k_1_A_p_3*R_p_3*L
![]()
a partial conversion rate of R''' in this transition
molecularity:=-1:
eq_Rp3_Ap3_1b:= dcRp3dt_1_A_p_3 = molecularity*Rate_1_A_p_3
![]()
the final form
eq_Rp3_Ap3_1c:= eq_Rp3_Ap3_1b | eq_Rp3_Ap3_1a
![]()
a reverse reaction rate for the transition
eq_Rp3_Ap3_2a:= Rate_2_A_p_3 = k_2_A_p_3*RL_p_3
![]()
a partial conversion rate of R''' in this transition
molecularity:=1:
eq_Rp3_Ap3_2b:= dcRp3dt_2_A_p_3 = molecularity*Rate_2_A_p_3
![]()
the final form
eq_Rp3_Ap3_2c:= eq_Rp3_Ap3_2b | eq_Rp3_Ap3_2a
![]()
R* <=> R'''
Constants: k_1_B_1_p_3 (forward), k_2_B_1_p_3 (reverse).
Equations subgroup: B1p3
a forward reaction rate for the transition
eq_Rp3_B1p3_1a:= Rate_1_B_1_p_3 = k_1_B_1_p_3*R_s
![]()
a partial conversion rate of R''' in this transition
molecularity:=1:
eq_Rp3_B1p3_1b:= dcRp3dt_1_B_1_p_3 = molecularity*Rate_1_B_1_p_3
![]()
the final form
eq_Rp3_B1p3_1c:= eq_Rp3_B1p3_1b | eq_Rp3_B1p3_1a
![]()
a reverse reaction rate for the transition
eq_Rp3_B1p3_2a:= Rate_2_B_1_p_3 = k_2_B_1_p_3*R_p_3
![]()
a partial conversion rate of R''' in this transition
molecularity:=-1:
eq_Rp3_B1p3_2b:= dcRp3dt_2_B_1_p_3 = molecularity*Rate_2_B_1_p_3
![]()
The final form
eq_Rp3_B1p3_2c:= eq_Rp3_B1p3_2b | eq_Rp3_B1p3_2a
![]()
R' <=> R'''
Constants: k_1_C_1_p_1_3 (forward), k_2_C_1_p_1_3 (reverse).
NOTE: Kinetic equations for this transition were already defined!
Equations subgroup: C1p13
a forward reaction rate for the transition
eq_Rp3_C1p13_1a:= eq_Rp1_C1p13_1a
![]()
a partial conversion rate of R''' in this transition
molecularity:=1:
eq_Rp3_C1p13_1b:= dcRp3dt_1_C_1_p_1_3 = molecularity*Rate_1_C_1_p_1_3
![]()
the final form
eq_Rp3_C1p13_1c:= eq_Rp3_C1p13_1b | eq_Rp3_C1p13_1a
![]()
a reverse reaction rate for the transition
eq_Rp3_C1p13_2a:= eq_Rp1_C1p13_2a
![]()
a partial conversion rate of R''' in this transition
molecularity:=-1:
eq_Rp3_C1p13_2b:= dcRp3dt_2_C_1_p_1_3 = molecularity*Rate_2_C_1_p_1_3
![]()
the final form
eq_Rp3_C1p13_2c:= eq_Rp3_C1p13_2b | eq_Rp3_C1p13_2a
![]()
R'' <=> R'''
Constants: k_1_C_1_p_2_3 (forward), k_2_C_1_p_2_3 (reverse).
NOTE: Kinetic equations for this transition were already defined!
Equations subgroup: C1p23
a forward reaction rate for the transition
eq_Rp3_C1p23_1a:= eq_Rp2_C1p23_1a
![]()
a partial conversion rate of R''' in this transition
molecularity:=1:
eq_Rp3_C1p23_1b:= dcRp3dt_1_C_1_p_2_3 = molecularity*Rate_1_C_1_p_2_3
![]()
the final form
eq_Rp3_C1p23_1c:= eq_Rp3_C1p23_1b | eq_Rp3_C1p23_1a
![]()
a reverse reaction rate for the transition
eq_Rp3_C1p23_2a:= eq_Rp2_C1p23_2a
![]()
a partial conversion rate of R''' in this transition
molecularity:=-1:
eq_Rp3_C1p23_2b:= dcRp3dt_2_C_1_p_2_3 = molecularity*Rate_2_C_1_p_2_3
![]()
the final form
eq_Rp3_C1p23_2c:= eq_Rp3_C1p23_2b | eq_Rp3_C1p23_2a
![]()
R''' <=> R''''
Constants: k_1_C_1_p_3_4 (forward), k_2_C_1_p_3_4 (reverse).
Equations subgroup: C1p34
a forward reaction rate for the transition
eq_Rp3_C1p34_1a:= Rate_1_C_1_p_3_4 = k_1_C_1_p_3_4*R_p_3
![]()
a partial conversion rate of R''' in this transition
molecularity:=-1:
eq_Rp3_C1p34_1b:= dcRp3dt_1_C_1_p_3_4 = molecularity*Rate_1_C_1_p_3_4
![]()
the final form
eq_Rp3_C1p34_1c:= eq_Rp3_C1p34_1b | eq_Rp3_C1p34_1a
![]()
a reverse reaction rate for the transition
eq_Rp3_C1p34_2a:= Rate_2_C_1_p_3_4 = k_2_C_1_p_3_4*R_p_4
![]()
a partial conversion rate of R''' in this transition
molecularity:=1:
eq_Rp3_C1p34_2b:= dcRp3dt_2_C_1_p_3_4 = molecularity*Rate_2_C_1_p_3_4
![]()
the final form
eq_Rp3_C1p34_2c:= eq_Rp3_C1p34_2b | eq_Rp3_C1p34_2a
![]()
R''' <=> R'''''
Constants: k_1_C_1_p_3_5 (forward), k_2_C_1_p_3_5 (reverse).
Equations subgroup: C1p35
a forward reaction rate for the transition
eq_Rp3_C1p35_1a:= Rate_1_C_1_p_3_5 = k_1_C_1_p_3_5*R_p_3
![]()
a partial conversion rate of R''' in this transition
molecularity:=-1:
eq_Rp3_C1p35_1b:= dcRp3dt_1_C_1_p_3_5 = molecularity*Rate_1_C_1_p_3_5
![]()
the final form
eq_Rp3_C1p35_1c:= eq_Rp3_C1p35_1b | eq_Rp3_C1p35_1a
![]()
a reverse reaction rate for the transition
eq_Rp3_C1p35_2a:= Rate_2_C_1_p_3_5 = k_2_C_1_p_3_5*R_p_5
![]()
a partial conversion rate of R''' in this transition
molecularity:=1:
eq_Rp3_C1p35_2b:= dcRp3dt_2_C_1_p_3_5 = molecularity*Rate_2_C_1_p_3_5
![]()
the final form
eq_Rp3_C1p35_2c:= eq_Rp3_C1p35_2b | eq_Rp3_C1p35_2a
![]()
Summary of partial conversion rates for the species
eq_Rp3_Ap3_1c;eq_Rp3_Ap3_2c;
![]()
![]()
eq_Rp3_B1p3_1c;eq_Rp3_B1p3_2c
![]()
![]()
eq_Rp3_C1p13_1c;eq_Rp3_C1p13_2c;
eq_Rp3_C1p23_1c;eq_Rp3_C1p23_2c;
eq_Rp3_C1p34_1c;eq_Rp3_C1p34_2c;
eq_Rp3_C1p35_1c;eq_Rp3_C1p35_2c;
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Net conversion rate for the species
I will create equations for all five versions of the mechanism.
1U-R-RL, 2U-R-RL - not needed (does not have R''' species)
3U-R-RL
dcRp3dt_N = dcRp3dt_1_A_p_3 + dcRp3dt_2_A_p_3 +\
dcRp3dt_1_B_1_p_3 + dcRp3dt_2_B_1_p_3 +\
dcRp3dt_1_C_1_p_1_3 + dcRp3dt_2_C_1_p_1_3 +\
dcRp3dt_1_C_1_p_2_3 + dcRp3dt_2_C_1_p_2_3 ;
![]()
Substitute (use all equations)
eq_Rp3_N__3U_R_RL:= % |\
eq_Rp3_Ap3_1c | eq_Rp3_Ap3_2c |\
eq_Rp3_B1p3_1c | eq_Rp3_B1p3_2c |\
eq_Rp3_C1p13_1c | eq_Rp3_C1p13_2c |\
eq_Rp3_C1p23_1c | eq_Rp3_C1p23_2c |\
eq_Rp3_C1p34_1c | eq_Rp3_C1p34_2c |\
eq_Rp3_C1p35_1c | eq_Rp3_C1p35_2c;
![]()
4U-R-RL
dcRp3dt_N = dcRp3dt_1_A_p_3 + dcRp3dt_2_A_p_3 +\
dcRp3dt_1_B_1_p_3 + dcRp3dt_2_B_1_p_3 +\
dcRp3dt_1_C_1_p_1_3 + dcRp3dt_2_C_1_p_1_3 +\
dcRp3dt_1_C_1_p_2_3 + dcRp3dt_2_C_1_p_2_3 +\
dcRp3dt_1_C_1_p_3_4 + dcRp3dt_2_C_1_p_3_4 ;

Substitute (use all equations)
eq_Rp3_N__4U_R_RL:= % |\
eq_Rp3_Ap3_1c | eq_Rp3_Ap3_2c |\
eq_Rp3_B1p3_1c | eq_Rp3_B1p3_2c |\
eq_Rp3_C1p13_1c | eq_Rp3_C1p13_2c |\
eq_Rp3_C1p23_1c | eq_Rp3_C1p23_2c |\
eq_Rp3_C1p34_1c | eq_Rp3_C1p34_2c |\
eq_Rp3_C1p35_1c | eq_Rp3_C1p35_2c;
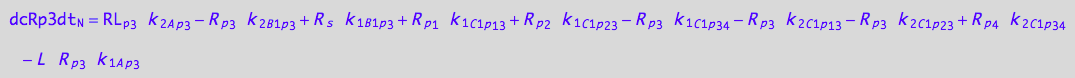
5U-R-RL
dcRp3dt_N = dcRp3dt_1_A_p_3 + dcRp3dt_2_A_p_3 +\
dcRp3dt_1_B_1_p_3 + dcRp3dt_2_B_1_p_3 +\
dcRp3dt_1_C_1_p_1_3 + dcRp3dt_2_C_1_p_1_3 +\
dcRp3dt_1_C_1_p_2_3 + dcRp3dt_2_C_1_p_2_3 +\
dcRp3dt_1_C_1_p_3_4 + dcRp3dt_2_C_1_p_3_4 +\
dcRp3dt_1_C_1_p_3_5 + dcRp3dt_2_C_1_p_3_5 ;

Substitute (use all equations)
eq_Rp3_N__5U_R_RL:= % |\
eq_Rp3_Ap3_1c | eq_Rp3_Ap3_2c |\
eq_Rp3_B1p3_1c | eq_Rp3_B1p3_2c |\
eq_Rp3_C1p13_1c | eq_Rp3_C1p13_2c |\
eq_Rp3_C1p23_1c | eq_Rp3_C1p23_2c |\
eq_Rp3_C1p34_1c | eq_Rp3_C1p34_2c |\
eq_Rp3_C1p35_1c | eq_Rp3_C1p35_2c;
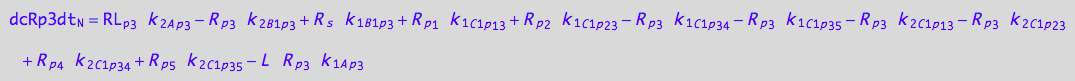
eq_Rp3_N__3U_R_RL
![]()
eq_Rp3_N__4U_R_RL
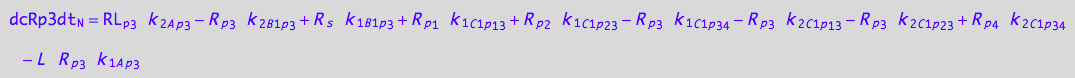
eq_Rp3_N__5U_R_RL
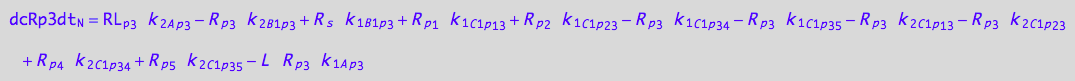
Back to Equations for each species
Equations group: Rp4
R''''+L<=>RL''''
Constants: k_1_A_p_4 (forward), k_2_A_p_4 (reverse).
Equations subgroup: Ap4
a forward reaction rate
eq_Rp4_Ap4_1a:= Rate_1_A_p_4 = k_1_A_p_4*R_p_4*L
![]()
a partial conversion rate of R'''' in this transition
molecularity:=-1:
eq_Rp4_Ap4_1b:= dcRp4dt_1_A_p_4 = molecularity*Rate_1_A_p_4
![]()
the final form
eq_Rp4_Ap4_1c:= eq_Rp4_Ap4_1b | eq_Rp4_Ap4_1a
![]()
a reverse reaction rate for the transition
eq_Rp4_Ap4_2a:= Rate_2_A_p_4 = k_2_A_p_4*RL_p_4
![]()
a partial conversion rate of R'''' in this transition
molecularity:=1:
eq_Rp4_Ap4_2b:= dcRp4dt_2_A_p_4 = molecularity*Rate_2_A_p_4
![]()
the final form
eq_Rp4_Ap4_2c:= eq_Rp4_Ap4_2b | eq_Rp4_Ap4_2a
![]()
R* <=> R''''
Constants: k_1_B_1_p_4 (forward), k_2_B_1_p_4 (reverse).
Equations subgroup: B1p4
a forward reaction rate for the transition
eq_Rp4_B1p4_1a:= Rate_1_B_1_p_4 = k_1_B_1_p_4*R_s
![]()
a partial conversion rate of R'''' in this transition
molecularity:=1:
eq_Rp4_B1p4_1b:= dcRp4dt_1_B_1_p_4 = molecularity*Rate_1_B_1_p_4
![]()
the final form
eq_Rp4_B1p4_1c:= eq_Rp4_B1p4_1b | eq_Rp4_B1p4_1a
![]()
a reverse reaction rate for the transition
eq_Rp4_B1p4_2a:= Rate_2_B_1_p_4 = k_2_B_1_p_4*R_p_4
![]()
a partial conversion rate of R'''' in this transition
molecularity:=-1:
eq_Rp4_B1p4_2b:= dcRp4dt_2_B_1_p_4 = molecularity*Rate_2_B_1_p_4
![]()
The final form
eq_Rp4_B1p4_2c:= eq_Rp4_B1p4_2b | eq_Rp4_B1p4_2a
![]()
R' <=> R''''
Constants: k_1_C_1_p_1_4 (forward), k_2_C_1_p_1_4 (reverse).
NOTE: Kinetic equations for this transition were already defined!
Equations subgroup: C1p14
a forward reaction rate for the transition
eq_Rp4_C1p14_1a:= eq_Rp1_C1p14_1a
![]()
a partial conversion rate of R'''' in this transition
molecularity:=1:
eq_Rp4_C1p14_1b:= dcRp4dt_1_C_1_p_1_4 = molecularity*Rate_1_C_1_p_1_4
![]()
the final form
eq_Rp4_C1p14_1c:= eq_Rp4_C1p14_1b | eq_Rp4_C1p14_1a
![]()
a reverse reaction rate for the transition
eq_Rp4_C1p14_2a:= eq_Rp1_C1p14_2a
![]()
a partial conversion rate of R'''' in this transition
molecularity:=-1:
eq_Rp4_C1p14_2b:= dcRp4dt_2_C_1_p_1_4 = molecularity*Rate_2_C_1_p_1_4
![]()
the final form
eq_Rp4_C1p14_2c:= eq_Rp4_C1p14_2b | eq_Rp4_C1p14_2a
![]()
R'' <=> R''''
Constants: k_1_C_1_p_2_4 (forward), k_2_C_1_p_2_4 (reverse).
NOTE: Kinetic equations for this transition were already defined!
Equations subgroup: C1p24
a forward reaction rate for the transition
eq_Rp4_C1p24_1a:= eq_Rp2_C1p24_1a
![]()
a partial conversion rate of R'''' in this transition
molecularity:=1:
eq_Rp4_C1p24_1b:= dcRp4dt_1_C_1_p_2_4 = molecularity*Rate_1_C_1_p_2_4
![]()
the final form
eq_Rp4_C1p24_1c:= eq_Rp4_C1p24_1b | eq_Rp4_C1p24_1a
![]()
a reverse reaction rate for the transition
eq_Rp4_C1p24_2a:= eq_Rp2_C1p24_2a
![]()
a partial conversion rate of R'''' in this transition
molecularity:=-1:
eq_Rp4_C1p24_2b:= dcRp4dt_2_C_1_p_2_4 = molecularity*Rate_2_C_1_p_2_4
![]()
the final form
eq_Rp4_C1p24_2c:= eq_Rp4_C1p24_2b | eq_Rp4_C1p24_2a
![]()
R''' <=> R''''
Constants: k_1_C_1_p_3_4 (forward), k_2_C_1_p_3_4 (reverse).
NOTE: Kinetic equations for this transition were already defined!
Equations subgroup: C1p34
a forward reaction rate for the transition
eq_Rp4_C1p34_1a:= eq_Rp3_C1p34_1a
![]()
a partial conversion rate of R'''' in this transition
molecularity:=1:
eq_Rp4_C1p34_1b:= dcRp4dt_1_C_1_p_3_4 = molecularity*Rate_1_C_1_p_3_4
![]()
the final form
eq_Rp4_C1p34_1c:= eq_Rp4_C1p34_1b | eq_Rp4_C1p34_1a
![]()
a reverse reaction rate for the transition
eq_Rp4_C1p34_2a:= eq_Rp3_C1p34_2a
![]()
a partial conversion rate of R'''' in this transition
molecularity:=-1:
eq_Rp4_C1p34_2b:= dcRp4dt_2_C_1_p_3_4 = molecularity*Rate_2_C_1_p_3_4
![]()
the final form
eq_Rp4_C1p34_2c:= eq_Rp4_C1p34_2b | eq_Rp4_C1p34_2a
![]()
R'''' <=> R'''''
Constants: k_1_C_1_p_4_5 (forward), k_2_C_1_p_4_5 (reverse).
Equations subgroup: C1p45
a forward reaction rate for the transition
eq_Rp4_C1p45_1a:= Rate_1_C_1_p_4_5 = k_1_C_1_p_4_5*R_p_4
![]()
a partial conversion rate of R'''' in this transition
molecularity:=-1:
eq_Rp4_C1p45_1b:= dcRp4dt_1_C_1_p_4_5 = molecularity*Rate_1_C_1_p_4_5
![]()
the final form
eq_Rp4_C1p45_1c:= eq_Rp4_C1p45_1b | eq_Rp4_C1p45_1a
![]()
a reverse reaction rate for the transition
eq_Rp4_C1p45_2a:= Rate_2_C_1_p_4_5 = k_2_C_1_p_4_5*R_p_5
![]()
a partial conversion rate of R'''' in this transition
molecularity:=1:
eq_Rp4_C1p45_2b:= dcRp4dt_2_C_1_p_4_5 = molecularity*Rate_2_C_1_p_4_5
![]()
the final form
eq_Rp4_C1p45_2c:= eq_Rp4_C1p45_2b | eq_Rp4_C1p45_2a
![]()
Summary of partial conversion rates for the species
eq_Rp4_Ap4_1c;eq_Rp4_Ap4_2c;
![]()
![]()
eq_Rp4_B1p4_1c;eq_Rp4_B1p4_2c
![]()
![]()
eq_Rp4_C1p14_1c;eq_Rp4_C1p14_2c;
eq_Rp4_C1p24_1c;eq_Rp4_C1p24_2c;
eq_Rp4_C1p34_1c;eq_Rp4_C1p34_2c;
eq_Rp4_C1p45_1c;eq_Rp4_C1p45_2c;
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Net conversion rate for the species
I will create equations for all five versions of the mechanism.
1U-R-RL, 2U-R-RL , 3U-R-RL - not needed (do not have R'''' species)
4U-R-RL
dcRp4dt_N = dcRp4dt_1_A_p_4 + dcRp4dt_2_A_p_4 +\
dcRp4dt_1_B_1_p_4 + dcRp4dt_2_B_1_p_4 +\
dcRp4dt_1_C_1_p_1_4 + dcRp4dt_2_C_1_p_1_4 +\
dcRp4dt_1_C_1_p_2_4 + dcRp4dt_2_C_1_p_2_4 +\
dcRp4dt_1_C_1_p_3_4 + dcRp4dt_2_C_1_p_3_4 ;

Substitute (use all equations)
eq_Rp4_N__4U_R_RL:= % |\
eq_Rp4_Ap4_1c | eq_Rp4_Ap4_2c |\
eq_Rp4_B1p4_1c | eq_Rp4_B1p4_2c |\
eq_Rp4_C1p14_1c | eq_Rp4_C1p14_2c |\
eq_Rp4_C1p24_1c | eq_Rp4_C1p24_2c |\
eq_Rp4_C1p34_1c | eq_Rp4_C1p34_2c |\
eq_Rp4_C1p45_1c | eq_Rp4_C1p45_2c;
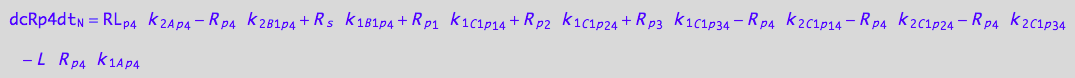
5U-R-RL
dcRp4dt_N = dcRp4dt_1_A_p_4 + dcRp4dt_2_A_p_4 +\
dcRp4dt_1_B_1_p_4 + dcRp4dt_2_B_1_p_4 +\
dcRp4dt_1_C_1_p_1_4 + dcRp4dt_2_C_1_p_1_4 +\
dcRp4dt_1_C_1_p_2_4 + dcRp4dt_2_C_1_p_2_4 +\
dcRp4dt_1_C_1_p_3_4 + dcRp4dt_2_C_1_p_3_4 +\
dcRp4dt_1_C_1_p_4_5 + dcRp4dt_2_C_1_p_4_5 ;

Substitute (use all equations)
eq_Rp4_N__5U_R_RL:= % |\
eq_Rp4_Ap4_1c | eq_Rp4_Ap4_2c |\
eq_Rp4_B1p4_1c | eq_Rp4_B1p4_2c |\
eq_Rp4_C1p14_1c | eq_Rp4_C1p14_2c |\
eq_Rp4_C1p24_1c | eq_Rp4_C1p24_2c |\
eq_Rp4_C1p34_1c | eq_Rp4_C1p34_2c |\
eq_Rp4_C1p45_1c | eq_Rp4_C1p45_2c;
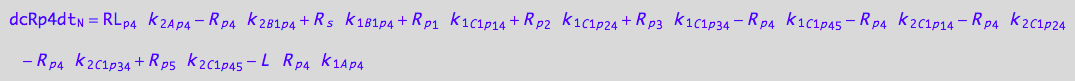
eq_Rp4_N__4U_R_RL
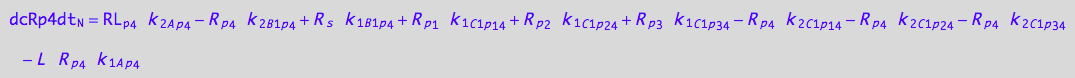
eq_Rp4_N__5U_R_RL
Back to Equations for each species
Equations group: Rp5
R'''''+L<=>RL'''''
Constants: k_1_A_p_5 (forward), k_2_A_p_5 (reverse).
Equations subgroup: Ap5
a forward reaction rate
eq_Rp5_Ap5_1a:= Rate_1_A_p_5 = k_1_A_p_5*R_p_5*L
![]()
a partial conversion rate of R''''' in this transition
molecularity:=-1:
eq_Rp5_Ap5_1b:= dcRp5dt_1_A_p_5 = molecularity*Rate_1_A_p_5
![]()
the final form
eq_Rp5_Ap5_1c:= eq_Rp5_Ap5_1b | eq_Rp5_Ap5_1a
![]()
a reverse reaction rate for the transition
eq_Rp5_Ap5_2a:= Rate_2_A_p_5 = k_2_A_p_5*RL_p_5
![]()
a partial conversion rate of R''''' in this transition
molecularity:=1:
eq_Rp5_Ap5_2b:= dcRp5dt_2_A_p_5 = molecularity*Rate_2_A_p_5
![]()
the final form
eq_Rp5_Ap5_2c:= eq_Rp5_Ap5_2b | eq_Rp5_Ap5_2a
![]()
R* <=> R'''''
Constants: k_1_B_1_p_5 (forward), k_2_B_1_p_5 (reverse).
Equations subgroup: B1p5
a forward reaction rate for the transition
eq_Rp5_B1p5_1a:= Rate_1_B_1_p_5 = k_1_B_1_p_5*R_s
![]()
a partial conversion rate of R''''' in this transition
molecularity:=1:
eq_Rp5_B1p5_1b:= dcRp5dt_1_B_1_p_5 = molecularity*Rate_1_B_1_p_5
![]()
the final form
eq_Rp5_B1p5_1c:= eq_Rp5_B1p5_1b | eq_Rp5_B1p5_1a
![]()
a reverse reaction rate for the transition
eq_Rp5_B1p5_2a:= Rate_2_B_1_p_5 = k_2_B_1_p_5*R_p_5
![]()
a partial conversion rate of R'''' in this transition
molecularity:=-1:
eq_Rp5_B1p5_2b:= dcRp5dt_2_B_1_p_5 = molecularity*Rate_2_B_1_p_5
![]()
The final form
eq_Rp5_B1p5_2c:= eq_Rp5_B1p5_2b | eq_Rp5_B1p5_2a
![]()
R' <=> R'''''
Constants: k_1_C_1_p_1_5 (forward), k_2_C_1_p_1_5 (reverse).
NOTE: Kinetic equations for this transition were already defined!
Equations subgroup: C1p15
a forward reaction rate for the transition
eq_Rp5_C1p15_1a:= eq_Rp1_C1p15_1a
![]()
a partial conversion rate of R''''' in this transition
molecularity:=1:
eq_Rp5_C1p15_1b:= dcRp5dt_1_C_1_p_1_5 = molecularity*Rate_1_C_1_p_1_5
![]()
the final form
eq_Rp5_C1p15_1c:= eq_Rp5_C1p15_1b | eq_Rp5_C1p15_1a
![]()
a reverse reaction rate for the transition
eq_Rp5_C1p15_2a:= eq_Rp1_C1p15_2a
![]()
a partial conversion rate of R''''' in this transition
molecularity:=-1:
eq_Rp5_C1p15_2b:= dcRp5dt_2_C_1_p_1_5 = molecularity*Rate_2_C_1_p_1_5
![]()
the final form
eq_Rp5_C1p15_2c:= eq_Rp5_C1p15_2b | eq_Rp5_C1p15_2a
![]()
R'' <=> R'''''
Constants: k_1_C_1_p_2_5 (forward), k_2_C_1_p_2_5 (reverse).
NOTE: Kinetic equations for this transition were already defined!
Equations subgroup: C1p25
a forward reaction rate for the transition
eq_Rp5_C1p25_1a:= eq_Rp2_C1p25_1a
![]()
a partial conversion rate of R''''' in this transition
molecularity:=1:
eq_Rp5_C1p25_1b:= dcRp5dt_1_C_1_p_2_5 = molecularity*Rate_1_C_1_p_2_5
![]()
the final form
eq_Rp5_C1p25_1c:= eq_Rp5_C1p25_1b | eq_Rp5_C1p25_1a
![]()
a reverse reaction rate for the transition
eq_Rp5_C1p25_2a:= eq_Rp2_C1p25_2a
![]()
a partial conversion rate of R''''' in this transition
molecularity:=-1:
eq_Rp5_C1p25_2b:= dcRp5dt_2_C_1_p_2_5 = molecularity*Rate_2_C_1_p_2_5
![]()
the final form
eq_Rp5_C1p25_2c:= eq_Rp5_C1p25_2b | eq_Rp5_C1p25_2a
![]()
R''' <=> R'''''
Constants: k_1_C_1_p_3_5 (forward), k_2_C_1_p_3_5 (reverse).
NOTE: Kinetic equations for this transition were already defined!
Equations subgroup: C1p35
a forward reaction rate for the transition
eq_Rp5_C1p35_1a:= eq_Rp3_C1p35_1a
![]()
a partial conversion rate of R''''' in this transition
molecularity:=1:
eq_Rp5_C1p35_1b:= dcRp5dt_1_C_1_p_3_5 = molecularity*Rate_1_C_1_p_3_5
![]()
the final form
eq_Rp5_C1p35_1c:= eq_Rp5_C1p35_1b | eq_Rp5_C1p35_1a
![]()
a reverse reaction rate for the transition
eq_Rp5_C1p35_2a:= eq_Rp3_C1p35_2a
![]()
a partial conversion rate of R''''' in this transition
molecularity:=-1:
eq_Rp5_C1p35_2b:= dcRp5dt_2_C_1_p_3_5 = molecularity*Rate_2_C_1_p_3_5
![]()
the final form
eq_Rp5_C1p35_2c:= eq_Rp5_C1p35_2b | eq_Rp5_C1p35_2a
![]()
R'''' <=> R'''''
Constants: k_1_C_1_p_3_5 (forward), k_2_C_1_p_3_5 (reverse).
NOTE: Kinetic equations for this transition were already defined!
Equations subgroup: C1p45
a forward reaction rate for the transition
eq_Rp5_C1p45_1a:= eq_Rp4_C1p45_1a
![]()
a partial conversion rate of R''''' in this transition
molecularity:=1:
eq_Rp5_C1p45_1b:= dcRp5dt_1_C_1_p_4_5 = molecularity*Rate_1_C_1_p_4_5
![]()
the final form
eq_Rp5_C1p45_1c:= eq_Rp5_C1p45_1b | eq_Rp5_C1p45_1a
![]()
a reverse reaction rate for the transition
eq_Rp5_C1p45_2a:= eq_Rp4_C1p45_2a
![]()
a partial conversion rate of R''''' in this transition
molecularity:=-1:
eq_Rp5_C1p45_2b:= dcRp5dt_2_C_1_p_4_5 = molecularity*Rate_2_C_1_p_4_5
![]()
the final form
eq_Rp5_C1p45_2c:= eq_Rp5_C1p45_2b | eq_Rp5_C1p45_2a
![]()
Summary of partial conversion rates for the species
eq_Rp5_Ap5_1c;eq_Rp5_Ap5_2c;
![]()
![]()
eq_Rp5_B1p5_1c;eq_Rp5_B1p5_2c
![]()
![]()
eq_Rp5_C1p15_1c;eq_Rp5_C1p15_2c;
eq_Rp5_C1p25_1c;eq_Rp5_C1p25_2c;
eq_Rp5_C1p35_1c;eq_Rp5_C1p35_2c;
eq_Rp5_C1p45_1c;eq_Rp5_C1p45_2c;
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Net conversion rate for the species
I will create equations for all five versions of the mechanism.
1U-R-RL, 2U-R-RL, 3U-R-RL, 4U-R-RL - not needed (do not have R'''' species)
5U-R-RL
dcRp5dt_N = dcRp5dt_1_A_p_5 + dcRp5dt_2_A_p_5 +\
dcRp5dt_1_B_1_p_5 + dcRp5dt_2_B_1_p_5 +\
dcRp5dt_1_C_1_p_1_5 + dcRp5dt_2_C_1_p_1_5 +\
dcRp5dt_1_C_1_p_2_5 + dcRp5dt_2_C_1_p_2_5 +\
dcRp5dt_1_C_1_p_3_5 + dcRp5dt_2_C_1_p_3_5 +\
dcRp5dt_1_C_1_p_4_5 + dcRp5dt_2_C_1_p_4_5 ;

Substitute (use all equations)
eq_Rp5_N__5U_R_RL:= % |\
eq_Rp5_Ap5_1c | eq_Rp5_Ap5_2c |\
eq_Rp5_B1p5_1c | eq_Rp5_B1p5_2c |\
eq_Rp5_C1p15_1c | eq_Rp5_C1p15_2c |\
eq_Rp5_C1p25_1c | eq_Rp5_C1p25_2c |\
eq_Rp5_C1p35_1c | eq_Rp5_C1p35_2c |\
eq_Rp5_C1p45_1c | eq_Rp5_C1p45_2c;

eq_Rp5_N__5U_R_RL

Back to Equations for each species
Equations group: RLp1
R'+L<=>RL'
Constants: k_1_A_p_1 (forward), k_2_A_p_1 (reverse).
NOTE: Kinetic equations for this transition were already defined!
Equations subgroup: Ap1
a forward reaction rate
eq_RLp1_Ap1_1a:= eq_Rp1_Ap1_1a
![]()
a partial conversion rate of RL' in this transition
molecularity:=1:
eq_RLp1_Ap1_1b:= dcRLp1dt_1_A_p_1 = molecularity*Rate_1_A_p_1
![]()
The final form
eq_RLp1_Ap1_1c:= eq_RLp1_Ap1_1b | eq_RLp1_Ap1_1a
![]()
a reverse reaction rate for the transition
eq_RLp1_Ap1_2a:= eq_Rp1_Ap1_2a
![]()
a partial conversion rate of RL' in this transition
molecularity:=-1:
eq_RLp1_Ap1_2b:= dcRLp1dt_2_A_p_1 = molecularity*Rate_2_A_p_1
![]()
The final form
eq_RLp1_Ap1_2c:= eq_RLp1_Ap1_2b | eq_RLp1_Ap1_2a
![]()
RL' <=> RL*
Constants: k_1_B_2_p_1 (forward), k_2_B_2_p_1 (reverse).
Equations subgroup: B2p1
a forward reaction rate for the transition
eq_RLp1_B2p1_1a:= Rate_1_B_2_p_1 = k_1_B_2_p_1*RL_p_1
![]()
a partial conversion rate of RL' in this transition
molecularity:=-1:
eq_RLp1_B2p1_1b:= dcRLp1dt_1_B_2_p_1 = molecularity*Rate_1_B_2_p_1
![]()
The final form
eq_RLp1_B2p1_1c:= eq_RLp1_B2p1_1b | eq_RLp1_B2p1_1a
![]()
a reverse reaction rate for the transition
eq_RLp1_B2p1_2a:= Rate_2_B_2_p_1 = k_2_B_2_p_1*RL_s
![]()
a partial conversion rate of RL' in this transition
molecularity:=1:
eq_RLp1_B2p1_2b:= dcRLp1dt_2_B_2_p_1 = molecularity*Rate_2_B_2_p_1
![]()
The final form
eq_RLp1_B2p1_2c:= eq_RLp1_B2p1_2b | eq_RLp1_B2p1_2a
![]()
RL' <=> RL''
Constants: k_1_C_2_p_1_2 (forward), k_2_C_2_p_1_2 (reverse).
Equations subgroup: C2p12
a forward reaction rate for the transition
eq_RLp1_C2p12_1a:= Rate_1_C_2_p_1_2 = k_1_C_2_p_1_2*RL_p_1
![]()
a partial conversion rate of RL' in this transition
molecularity:=-1:
eq_RLp1_C2p12_1b:= dcRLp1dt_1_C_2_p_1_2 = molecularity*Rate_1_C_2_p_1_2
![]()
The final form
eq_RLp1_C2p12_1c:= eq_RLp1_C2p12_1b | eq_RLp1_C2p12_1a
![]()
a reverse reaction rate for the transition
eq_RLp1_C2p12_2a:= Rate_2_C_2_p_1_2 = k_2_C_2_p_1_2*RL_p_2
![]()
a partial conversion rate of RL' in this transition
molecularity:=1:
eq_RLp1_C2p12_2b:= dcRLp1dt_2_C_2_p_1_2 = molecularity*Rate_2_C_2_p_1_2
![]()
The final form
eq_RLp1_C2p12_2c:= eq_RLp1_C2p12_2b | eq_RLp1_C2p12_2a
![]()
RL' <=> RL'''
Constants: k_1_C_2_p_1_3 (forward), k_2_C_2_p_1_3 (reverse).
Equations subgroup: C2p13
a forward reaction rate for the transition
eq_RLp1_C2p13_1a:= Rate_1_C_2_p_1_3 = k_1_C_2_p_1_3*RL_p_1
![]()
a partial conversion rate of RL' in this transition
molecularity:=-1:
eq_RLp1_C2p13_1b:= dcRLp1dt_1_C_2_p_1_3 = molecularity*Rate_1_C_2_p_1_3
![]()
The final form
eq_RLp1_C2p13_1c:= eq_RLp1_C2p13_1b | eq_RLp1_C2p13_1a
![]()
a reverse reaction rate for the transition
eq_RLp1_C2p13_2a:= Rate_2_C_2_p_1_3 = k_2_C_2_p_1_3*RL_p_3
![]()
a partial conversion rate of RL' in this transition
molecularity:=1:
eq_RLp1_C2p13_2b:= dcRLp1dt_2_C_2_p_1_3 = molecularity*Rate_2_C_2_p_1_3
![]()
The final form
eq_RLp1_C2p13_2c:= eq_RLp1_C2p13_2b | eq_RLp1_C2p13_2a
![]()
RL' <=> RL''''
Constants: k_1_C_2_p_1_4 (forward), k_2_C_2_p_1_4 (reverse).
Equations subgroup: C2p14
a forward reaction rate for the transition
eq_RLp1_C2p14_1a:= Rate_1_C_2_p_1_4 = k_1_C_2_p_1_4*RL_p_1
![]()
a partial conversion rate of RL' in this transition
molecularity:=-1:
eq_RLp1_C2p14_1b:= dcRLp1dt_1_C_2_p_1_4 = molecularity*Rate_1_C_2_p_1_4
![]()
The final form
eq_RLp1_C2p14_1c:= eq_RLp1_C2p14_1b | eq_RLp1_C2p14_1a
![]()
a reverse reaction rate for the transition
eq_RLp1_C2p14_2a:= Rate_2_C_2_p_1_4 = k_2_C_2_p_1_4*RL_p_4
![]()
a partial conversion rate of RL' in this transition
molecularity:=1:
eq_RLp1_C2p14_2b:= dcRLp1dt_2_C_2_p_1_4 = molecularity*Rate_2_C_2_p_1_4
![]()
The final form
eq_RLp1_C2p14_2c:= eq_RLp1_C2p14_2b | eq_RLp1_C2p14_2a
![]()
RL' <=> RL'''''
Constants: k_1_C_2_p_1_5 (forward), k_2_C_2_p_1_5 (reverse).
Equations subgroup: C2p15
a forward reaction rate for the transition
eq_RLp1_C2p15_1a:= Rate_1_C_2_p_1_5 = k_1_C_2_p_1_5*RL_p_1
![]()
a partial conversion rate of RL' in this transition
molecularity:=-1:
eq_RLp1_C2p15_1b:= dcRLp1dt_1_C_2_p_1_5 = molecularity*Rate_1_C_2_p_1_5
![]()
The final form
eq_RLp1_C2p15_1c:= eq_RLp1_C2p15_1b | eq_RLp1_C2p15_1a
![]()
a reverse reaction rate for the transition
eq_RLp1_C2p15_2a:= Rate_2_C_2_p_1_5 = k_2_C_2_p_1_5*RL_p_5
![]()
a partial conversion rate of RL' in this transition
molecularity:=1:
eq_RLp1_C2p15_2b:= dcRLp1dt_2_C_2_p_1_5 = molecularity*Rate_2_C_2_p_1_5
![]()
The final form
eq_RLp1_C2p15_2c:= eq_RLp1_C2p15_2b | eq_RLp1_C2p15_2a
![]()
Summary of partial conversion rates for the species
eq_RLp1_Ap1_1c;eq_RLp1_Ap1_2c;
![]()
![]()
eq_RLp1_B2p1_1c;eq_RLp1_B2p1_2c
![]()
![]()
eq_RLp1_C2p12_1c;eq_RLp1_C2p12_2c;
eq_RLp1_C2p13_1c;eq_RLp1_C2p13_2c;
eq_RLp1_C2p14_1c;eq_RLp1_C2p14_2c;
eq_RLp1_C2p15_1c;eq_RLp1_C2p15_2c;
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Net conversion rate for the species
I will create equations for all five versions of the mechanism.
1U-R-RL
dcRLp1dt_N = dcRLp1dt_1_A_p_1 + dcRLp1dt_2_A_p_1 + dcRLp1dt_1_B_2_p_1 + dcRLp1dt_2_B_2_p_1
![]()
Substitute (use all equations)
eq_RLp1_N__1U_R_RL:= % | eq_RLp1_Ap1_1c | eq_RLp1_Ap1_2c \
| eq_RLp1_B2p1_1c | eq_RLp1_B2p1_2c \
| eq_RLp1_C2p12_1c | eq_RLp1_C2p12_2c \
| eq_RLp1_C2p13_1c | eq_RLp1_C2p13_2c \
| eq_RLp1_C2p14_1c | eq_RLp1_C2p14_2c \
| eq_RLp1_C2p15_1c | eq_RLp1_C2p15_2c;
![]()
2U-R-RL
dcRLp1dt_N = dcRLp1dt_1_A_p_1 + dcRLp1dt_2_A_p_1 + dcRLp1dt_1_B_2_p_1 + dcRLp1dt_2_B_2_p_1 +\
dcRLp1dt_1_C_2_p_1_2 + dcRLp1dt_2_C_2_p_1_2;
![]()
Substitute (use all equations)
eq_RLp1_N__2U_R_RL:= % | eq_RLp1_Ap1_1c | eq_RLp1_Ap1_2c \
| eq_RLp1_B2p1_1c | eq_RLp1_B2p1_2c \
| eq_RLp1_C2p12_1c | eq_RLp1_C2p12_2c \
| eq_RLp1_C2p13_1c | eq_RLp1_C2p13_2c \
| eq_RLp1_C2p14_1c | eq_RLp1_C2p14_2c \
| eq_RLp1_C2p15_1c | eq_RLp1_C2p15_2c;
![]()
3U-R-RL
dcRLp1dt_N = dcRLp1dt_1_A_p_1 + dcRLp1dt_2_A_p_1 + dcRLp1dt_1_B_2_p_1 + dcRLp1dt_2_B_2_p_1 +\
dcRLp1dt_1_C_2_p_1_2 + dcRLp1dt_2_C_2_p_1_2 +\
dcRLp1dt_1_C_2_p_1_3 + dcRLp1dt_2_C_2_p_1_3;
![]()
Substitute (use all equations)
eq_RLp1_N__3U_R_RL:= % | eq_RLp1_Ap1_1c | eq_RLp1_Ap1_2c \
| eq_RLp1_B2p1_1c | eq_RLp1_B2p1_2c \
| eq_RLp1_C2p12_1c | eq_RLp1_C2p12_2c \
| eq_RLp1_C2p13_1c | eq_RLp1_C2p13_2c \
| eq_RLp1_C2p14_1c | eq_RLp1_C2p14_2c \
| eq_RLp1_C2p15_1c | eq_RLp1_C2p15_2c;
![]()
4U-R-RL
dcRLp1dt_N = dcRLp1dt_1_A_p_1 + dcRLp1dt_2_A_p_1 + dcRLp1dt_1_B_2_p_1 + dcRLp1dt_2_B_2_p_1 +\
dcRLp1dt_1_C_2_p_1_2 + dcRLp1dt_2_C_2_p_1_2 +\
dcRLp1dt_1_C_2_p_1_3 + dcRLp1dt_2_C_2_p_1_3 +\
dcRLp1dt_1_C_2_p_1_4 + dcRLp1dt_2_C_2_p_1_4;

Substitute (use all equations)
eq_RLp1_N__4U_R_RL:= % | eq_RLp1_Ap1_1c | eq_RLp1_Ap1_2c \
| eq_RLp1_B2p1_1c | eq_RLp1_B2p1_2c \
| eq_RLp1_C2p12_1c | eq_RLp1_C2p12_2c \
| eq_RLp1_C2p13_1c | eq_RLp1_C2p13_2c \
| eq_RLp1_C2p14_1c | eq_RLp1_C2p14_2c \
| eq_RLp1_C2p15_1c | eq_RLp1_C2p15_2c;

5U-R-RL
dcRLp1dt_N = dcRLp1dt_1_A_p_1 + dcRLp1dt_2_A_p_1 + dcRLp1dt_1_B_2_p_1 + dcRLp1dt_2_B_2_p_1 +\
dcRLp1dt_1_C_2_p_1_2 + dcRLp1dt_2_C_2_p_1_2 +\
dcRLp1dt_1_C_2_p_1_3 + dcRLp1dt_2_C_2_p_1_3 +\
dcRLp1dt_1_C_2_p_1_4 + dcRLp1dt_2_C_2_p_1_4 +\
dcRLp1dt_1_C_2_p_1_5 + dcRLp1dt_2_C_2_p_1_5;

Substitute (use all equations)
eq_RLp1_N__5U_R_RL:= % | eq_RLp1_Ap1_1c | eq_RLp1_Ap1_2c \
| eq_RLp1_B2p1_1c | eq_RLp1_B2p1_2c \
| eq_RLp1_C2p12_1c | eq_RLp1_C2p12_2c \
| eq_RLp1_C2p13_1c | eq_RLp1_C2p13_2c \
| eq_RLp1_C2p14_1c | eq_RLp1_C2p14_2c \
| eq_RLp1_C2p15_1c | eq_RLp1_C2p15_2c;

eq_RLp1_N__1U_R_RL
![]()
eq_RLp1_N__2U_R_RL
![]()
eq_RLp1_N__3U_R_RL
![]()
eq_RLp1_N__4U_R_RL

eq_RLp1_N__5U_R_RL

Back to Equations for each species
Equations group: RLp2
R''+L<=>RL''
Constants: k_1_A_p_2 (forward), k_2_A_p_2 (reverse).
NOTE: Kinetic equations for this transition were already defined!
Equations subgroup: Ap2
a forward reaction rate
eq_RLp2_Ap2_1a:= eq_Rp2_Ap2_1a
![]()
a partial conversion rate of RL'' in this transition
molecularity:=1:
eq_RLp2_Ap2_1b:= dcRLp2dt_1_A_p_2 = molecularity*Rate_1_A_p_2
![]()
the final form
eq_RLp2_Ap2_1c:= eq_RLp2_Ap2_1b | eq_RLp2_Ap2_1a
![]()
a reverse reaction rate for the transition
eq_RLp2_Ap2_2a:= eq_Rp2_Ap2_2a
![]()
a partial conversion rate of RL'' in this transition
molecularity:=-1:
eq_RLp2_Ap2_2b:= dcRLp2dt_2_A_p_2 = molecularity*Rate_2_A_p_2
![]()
the final form
eq_RLp2_Ap2_2c:= eq_RLp2_Ap2_2b | eq_RLp2_Ap2_2a
![]()
RL'' <=> RL*
Constants: k_1_B_2_p_2 (forward), k_2_B_2_p_2 (reverse).
Equations subgroup: B2p2
a forward reaction rate for the transition
eq_RLp2_B2p2_1a:= Rate_1_B_2_p_2 = k_1_B_2_p_2*RL_p_2
![]()
a partial conversion rate of RL'' in this transition
molecularity:=-1:
eq_RLp2_B2p2_1b:= dcRLp2dt_1_B_2_p_2 = molecularity*Rate_1_B_2_p_2
![]()
the final form
eq_RLp2_B2p2_1c:= eq_RLp2_B2p2_1b | eq_RLp2_B2p2_1a
![]()
a reverse reaction rate for the transition
eq_RLp2_B2p2_2a:= Rate_2_B_2_p_2 = k_2_B_2_p_2*RL_s
![]()
a partial conversion rate of RL'' in this transition
molecularity:=1:
eq_RLp2_B2p2_2b:= dcRLp2dt_2_B_2_p_2 = molecularity*Rate_2_B_2_p_2
![]()
the final form
eq_RLp2_B2p2_2c:= eq_RLp2_B2p2_2b | eq_RLp2_B2p2_2a
![]()
RL' <=> RL''
Constants: k_1_C_2_p_1_2 (forward), k_2_C_2_p_1_2 (reverse).
NOTE: Kinetic equations for this transition were already defined!
Equations subgroup: C2p12
a forward reaction rate for the transition
eq_RLp2_C2p12_1a:= eq_RLp1_C2p12_1a
![]()
a partial conversion rate of RL'' in this transition
molecularity:=1:
eq_RLp2_C2p12_1b:= dcRLp2dt_1_C_2_p_1_2 = molecularity*Rate_1_C_2_p_1_2
![]()
the final form
eq_RLp2_C2p12_1c:= eq_RLp2_C2p12_1b | eq_RLp2_C2p12_1a
![]()
a reverse reaction rate for the transition
eq_RLp2_C2p12_2a:= eq_RLp1_C2p12_2a
![]()
a partial conversion rate of RL'' in this transition
molecularity:=-1:
eq_RLp2_C2p12_2b:= dcRLp2dt_2_C_2_p_1_2 = molecularity*Rate_2_C_2_p_1_2
![]()
the final form
eq_RLp2_C2p12_2c:= eq_RLp2_C2p12_2b | eq_RLp2_C2p12_2a
![]()
RL'' <=> RL'''
Constants: k_1_C_2_p_2_3 (forward), k_2_C_2_p_2_3 (reverse).
Equations subgroup: C2p23
a forward reaction rate for the transition
eq_RLp2_C2p23_1a:= Rate_1_C_2_p_2_3 = k_1_C_2_p_2_3*RL_p_2
![]()
a partial conversion rate of RL'' in this transition
molecularity:=-1:
eq_RLp2_C2p23_1b:= dcRLp2dt_1_C_2_p_2_3 = molecularity*Rate_1_C_2_p_2_3
![]()
the final form
eq_RLp2_C2p23_1c:= eq_RLp2_C2p23_1b | eq_RLp2_C2p23_1a
![]()
a reverse reaction rate for the transition
eq_RLp2_C2p23_2a:= Rate_2_C_2_p_2_3 = k_2_C_2_p_2_3*RL_p_3
![]()
a partial conversion rate of RL'' in this transition
molecularity:=1:
eq_RLp2_C2p23_2b:= dcRLp2dt_2_C_2_p_2_3 = molecularity*Rate_2_C_2_p_2_3
![]()
the final form
eq_RLp2_C2p23_2c:= eq_RLp2_C2p23_2b | eq_RLp2_C2p23_2a
![]()
RL'' <=> RL''''
Constants: k_1_C_2_p_2_4 (forward), k_2_C_2_p_2_4 (reverse).
Equations subgroup: C2p24
a forward reaction rate for the transition
eq_RLp2_C2p24_1a:= Rate_1_C_2_p_2_4 = k_1_C_2_p_2_4*RL_p_2
![]()
a partial conversion rate of RL'' in this transition
molecularity:=-1:
eq_RLp2_C2p24_1b:= dcRLp2dt_1_C_2_p_2_4 = molecularity*Rate_1_C_2_p_2_4
![]()
the final form
eq_RLp2_C2p24_1c:= eq_RLp2_C2p24_1b | eq_RLp2_C2p24_1a
![]()
a reverse reaction rate for the transition
eq_RLp2_C2p24_2a:= Rate_2_C_2_p_2_4 = k_2_C_2_p_2_4*RL_p_4
![]()
a partial conversion rate of RL'' in this transition
molecularity:=1:
eq_RLp2_C2p24_2b:= dcRLp2dt_2_C_2_p_2_4 = molecularity*Rate_2_C_2_p_2_4
![]()
the final form
eq_RLp2_C2p24_2c:= eq_RLp2_C2p24_2b | eq_RLp2_C2p24_2a
![]()
RL'' <=> RL'''''
Constants: k_1_C_2_p_2_5 (forward), k_2_C_2_p_2_5 (reverse).
Equations subgroup: C2p25
a forward reaction rate for the transition
eq_RLp2_C2p25_1a:= Rate_1_C_2_p_2_5 = k_1_C_2_p_2_5*RL_p_2
![]()
a partial conversion rate of RL'' in this transition
molecularity:=-1:
eq_RLp2_C2p25_1b:= dcRLp2dt_1_C_2_p_2_5 = molecularity*Rate_1_C_2_p_2_5
![]()
the final form
eq_RLp2_C2p25_1c:= eq_RLp2_C2p25_1b | eq_RLp2_C2p25_1a
![]()
a reverse reaction rate for the transition
eq_RLp2_C2p25_2a:= Rate_2_C_2_p_2_5 = k_2_C_2_p_2_5*RL_p_5
![]()
a partial conversion rate of RL'' in this transition
molecularity:=1:
eq_RLp2_C2p25_2b:= dcRLp2dt_2_C_2_p_2_5 = molecularity*Rate_2_C_2_p_2_5
![]()
the final form
eq_RLp2_C2p25_2c:= eq_RLp2_C2p25_2b | eq_RLp2_C2p25_2a
![]()
Summary of partial conversion rates for the species
eq_RLp2_Ap2_1c;eq_RLp2_Ap2_2c;
![]()
![]()
eq_RLp2_B2p2_1c;eq_RLp2_B2p2_2c
![]()
![]()
eq_RLp2_C2p12_1c;eq_RLp2_C2p12_2c;
eq_RLp2_C2p23_1c;eq_RLp2_C2p23_2c;
eq_RLp2_C2p24_1c;eq_RLp2_C2p24_2c;
eq_RLp2_C2p25_1c;eq_RLp2_C2p25_2c;
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Net conversion rate for the species
I will create equations for all five versions of the mechanism.
1U-R-RL - not needed; no RL'' species
2U-R-RL
dcRLp2dt_N = dcRLp2dt_1_A_p_2 + dcRLp2dt_2_A_p_2 + dcRLp2dt_1_B_2_p_2 + dcRLp2dt_2_B_2_p_2 +\
dcRLp2dt_1_C_2_p_1_2 + dcRLp2dt_2_C_2_p_1_2;
![]()
Substitute (use all equations)
eq_RLp2_N__2U_R_RL:= % | eq_RLp2_Ap2_1c | eq_RLp2_Ap2_2c \
| eq_RLp2_B2p2_1c | eq_RLp2_B2p2_2c \
| eq_RLp2_C2p12_1c | eq_RLp2_C2p12_2c \
| eq_RLp2_C2p23_1c | eq_RLp2_C2p23_2c \
| eq_RLp2_C2p24_1c | eq_RLp2_C2p24_2c \
| eq_RLp2_C2p25_1c | eq_RLp2_C2p25_2c;
![]()
3U-R-RL
dcRLp2dt_N = dcRLp2dt_1_A_p_2 + dcRLp2dt_2_A_p_2 + dcRLp2dt_1_B_2_p_2 + dcRLp2dt_2_B_2_p_2 +\
dcRLp2dt_1_C_2_p_1_2 + dcRLp2dt_2_C_2_p_1_2 +\
dcRLp2dt_1_C_2_p_2_3 + dcRLp2dt_2_C_2_p_2_3;
![]()
Substitute (use all equations)
eq_RLp2_N__3U_R_RL:= % | eq_RLp2_Ap2_1c | eq_RLp2_Ap2_2c \
| eq_RLp2_B2p2_1c | eq_RLp2_B2p2_2c \
| eq_RLp2_C2p12_1c | eq_RLp2_C2p12_2c \
| eq_RLp2_C2p23_1c | eq_RLp2_C2p23_2c \
| eq_RLp2_C2p24_1c | eq_RLp2_C2p24_2c \
| eq_RLp2_C2p25_1c | eq_RLp2_C2p25_2c;
![]()
4U-R-RL
dcRLp2dt_N = dcRLp2dt_1_A_p_2 + dcRLp2dt_2_A_p_2 + dcRLp2dt_1_B_2_p_2 + dcRLp2dt_2_B_2_p_2 +\
dcRLp2dt_1_C_2_p_1_2 + dcRLp2dt_2_C_2_p_1_2 +\
dcRLp2dt_1_C_2_p_2_3 + dcRLp2dt_2_C_2_p_2_3 +\
dcRLp2dt_1_C_2_p_2_4 + dcRLp2dt_2_C_2_p_2_4;

Substitute (use all equations)
eq_RLp2_N__4U_R_RL:= % | eq_RLp2_Ap2_1c | eq_RLp2_Ap2_2c \
| eq_RLp2_B2p2_1c | eq_RLp2_B2p2_2c \
| eq_RLp2_C2p12_1c | eq_RLp2_C2p12_2c \
| eq_RLp2_C2p23_1c | eq_RLp2_C2p23_2c \
| eq_RLp2_C2p24_1c | eq_RLp2_C2p24_2c \
| eq_RLp2_C2p25_1c | eq_RLp2_C2p25_2c;

5U-R-RL
dcRLp2dt_N = dcRLp2dt_1_A_p_2 + dcRLp2dt_2_A_p_2 + dcRLp2dt_1_B_2_p_2 + dcRLp2dt_2_B_2_p_2 +\
dcRLp2dt_1_C_2_p_1_2 + dcRLp2dt_2_C_2_p_1_2 +\
dcRLp2dt_1_C_2_p_2_3 + dcRLp2dt_2_C_2_p_2_3 +\
dcRLp2dt_1_C_2_p_2_4 + dcRLp2dt_2_C_2_p_2_4 +\
dcRLp2dt_1_C_2_p_2_5 + dcRLp2dt_2_C_2_p_2_5;

Substitute (use all equations)
eq_RLp2_N__5U_R_RL:= % | eq_RLp2_Ap2_1c | eq_RLp2_Ap2_2c \
| eq_RLp2_B2p2_1c | eq_RLp2_B2p2_2c \
| eq_RLp2_C2p12_1c | eq_RLp2_C2p12_2c \
| eq_RLp2_C2p23_1c | eq_RLp2_C2p23_2c \
| eq_RLp2_C2p24_1c | eq_RLp2_C2p24_2c \
| eq_RLp2_C2p25_1c | eq_RLp2_C2p25_2c;

eq_RLp2_N__2U_R_RL
![]()
eq_RLp2_N__3U_R_RL
![]()
eq_RLp2_N__4U_R_RL

eq_RLp2_N__5U_R_RL

Back to Equations for each species
Equations group: RLp3
R'''+L<=>RL'''
Constants: k_1_A_p_3 (forward), k_2_A_p_3 (reverse).
NOTE: Kinetic equations for this transition were already defined!
Equations subgroup: Ap3
a forward reaction rate
eq_RLp3_Ap3_1a:= eq_Rp3_Ap3_1a
![]()
a partial conversion rate of RL''' in this transition
molecularity:=1:
eq_RLp3_Ap3_1b:= dcRLp3dt_1_A_p_3 = molecularity*Rate_1_A_p_3
![]()
the final form
eq_RLp3_Ap3_1c:= eq_RLp3_Ap3_1b | eq_RLp3_Ap3_1a
![]()
a reverse reaction rate for the transition
eq_RLp3_Ap3_2a:= eq_Rp3_Ap3_2a
![]()
a partial conversion rate of RL''' in this transition
molecularity:=-1:
eq_RLp3_Ap3_2b:= dcRLp3dt_2_A_p_3 = molecularity*Rate_2_A_p_3
![]()
the final form
eq_RLp3_Ap3_2c:= eq_RLp3_Ap3_2b | eq_RLp3_Ap3_2a
![]()
RL''' <=> RL*
Constants: k_1_B_2_p_3 (forward), k_2_B_2_p_3 (reverse).
Equations subgroup: B2p3
a forward reaction rate for the transition
eq_RLp3_B2p3_1a:= Rate_1_B_2_p_3 = k_1_B_2_p_3*RL_p_3
![]()
a partial conversion rate of RL''' in this transition
molecularity:=-1:
eq_RLp3_B2p3_1b:= dcRLp3dt_1_B_2_p_3 = molecularity*Rate_1_B_2_p_3
![]()
the final form
eq_RLp3_B2p3_1c:= eq_RLp3_B2p3_1b | eq_RLp3_B2p3_1a
![]()
a reverse reaction rate for the transition
eq_RLp3_B2p3_2a:= Rate_2_B_2_p_3 = k_2_B_2_p_3*RL_s
![]()
a partial conversion rate of RL''' in this transition
molecularity:=1:
eq_RLp3_B2p3_2b:= dcRLp3dt_2_B_2_p_3 = molecularity*Rate_2_B_2_p_3
![]()
the final form
eq_RLp3_B2p3_2c:= eq_RLp3_B2p3_2b | eq_RLp3_B2p3_2a
![]()
RL' <=> RL'''
Constants: k_1_C_2_p_1_3 (forward), k_2_C_2_p_1_3 (reverse).
NOTE: Kinetic equations for this transition were already defined!
Equations subgroup: C2p13
a forward reaction rate for the transition
eq_RLp3_C2p13_1a:= eq_RLp1_C2p13_1a
![]()
a partial conversion rate of RL''' in this transition
molecularity:=1:
eq_RLp3_C2p13_1b:= dcRLp3dt_1_C_2_p_1_3 = molecularity*Rate_1_C_2_p_1_3
![]()
the final form
eq_RLp3_C2p13_1c:= eq_RLp3_C2p13_1b | eq_RLp3_C2p13_1a
![]()
a reverse reaction rate for the transition
eq_RLp3_C2p13_2a:= eq_RLp1_C2p13_2a
![]()
a partial conversion rate of RL''' in this transition
molecularity:=-1:
eq_RLp3_C2p13_2b:= dcRLp3dt_2_C_2_p_1_3 = molecularity*Rate_2_C_2_p_1_3
![]()
the final form
eq_RLp3_C2p13_2c:= eq_RLp3_C2p13_2b | eq_RLp3_C2p13_2a
![]()
RL'' <=> RL'''
Constants: k_1_C_2_p_2_3 (forward), k_2_C_2_p_2_3 (reverse).
NOTE: Kinetic equations for this transition were already defined!
Equations subgroup: C2p23
a forward reaction rate for the transition
eq_RLp3_C2p23_1a:= eq_RLp2_C2p23_1a
![]()
a partial conversion rate of RL''' in this transition
molecularity:=1:
eq_RLp3_C2p23_1b:= dcRLp3dt_1_C_2_p_2_3 = molecularity*Rate_1_C_2_p_2_3
![]()
the final form
eq_RLp3_C2p23_1c:= eq_RLp3_C2p23_1b | eq_RLp3_C2p23_1a
![]()
a reverse reaction rate for the transition
eq_RLp3_C2p23_2a:= eq_RLp2_C2p23_2a
![]()
a partial conversion rate of RL''' in this transition
molecularity:=-1:
eq_RLp3_C2p23_2b:= dcRLp3dt_2_C_2_p_2_3 = molecularity*Rate_2_C_2_p_2_3
![]()
the final form
eq_RLp3_C2p23_2c:= eq_RLp3_C2p23_2b | eq_RLp3_C2p23_2a
![]()
RL''' <=> RL''''
Constants: k_1_C_2_p_3_4 (forward), k_2_C_2_p_3_4 (reverse).
Equations subgroup: C2p34
a forward reaction rate for the transition
eq_RLp3_C2p34_1a:= Rate_1_C_2_p_3_4 = k_1_C_2_p_3_4*RL_p_3
![]()
a partial conversion rate of RL''' in this transition
molecularity:=-1:
eq_RLp3_C2p34_1b:= dcRLp3dt_1_C_2_p_3_4 = molecularity*Rate_1_C_2_p_3_4
![]()
the final form
eq_RLp3_C2p34_1c:= eq_RLp3_C2p34_1b | eq_RLp3_C2p34_1a
![]()
a reverse reaction rate for the transition
eq_RLp3_C2p34_2a:= Rate_2_C_2_p_3_4 = k_2_C_2_p_3_4*RL_p_4
![]()
a partial conversion rate of RL''' in this transition
molecularity:=1:
eq_RLp3_C2p34_2b:= dcRLp3dt_2_C_2_p_3_4 = molecularity*Rate_2_C_2_p_3_4
![]()
the final form
eq_RLp3_C2p34_2c:= eq_RLp3_C2p34_2b | eq_RLp3_C2p34_2a
![]()
RL''' <=> RL'''''
Constants: k_1_C_2_p_3_5 (forward), k_2_C_2_p_3_5 (reverse).
Equations subgroup: C2p35
a forward reaction rate for the transition
eq_RLp3_C2p35_1a:= Rate_1_C_2_p_3_5 = k_1_C_2_p_3_5*RL_p_3
![]()
a partial conversion rate of RL''' in this transition
molecularity:=-1:
eq_RLp3_C2p35_1b:= dcRLp3dt_1_C_2_p_3_5 = molecularity*Rate_1_C_2_p_3_5
![]()
the final form
eq_RLp3_C2p35_1c:= eq_RLp3_C2p35_1b | eq_RLp3_C2p35_1a
![]()
a reverse reaction rate for the transition
eq_RLp3_C2p35_2a:= Rate_2_C_2_p_3_5 = k_2_C_2_p_3_5*RL_p_5
![]()
a partial conversion rate of RL''' in this transition
molecularity:=1:
eq_RLp3_C2p35_2b:= dcRLp3dt_2_C_2_p_3_5 = molecularity*Rate_2_C_2_p_3_5
![]()
the final form
eq_RLp3_C2p35_2c:= eq_RLp3_C2p35_2b | eq_RLp3_C2p35_2a
![]()
Summary of partial conversion rates for the species
eq_RLp3_Ap3_1c;eq_RLp3_Ap3_2c;
![]()
![]()
eq_RLp3_B2p3_1c;eq_RLp3_B2p3_2c
![]()
![]()
eq_RLp3_C2p13_1c;eq_RLp3_C2p13_2c;
eq_RLp3_C2p23_1c;eq_RLp3_C2p23_2c;
eq_RLp3_C2p34_1c;eq_RLp3_C2p34_2c;
eq_RLp3_C2p35_1c;eq_RLp3_C2p35_2c;
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Net conversion rate for the species
I will create equations for all five versions of the mechanism.
1U-R-RL, 2U-R-RL - not needed; no RL''' species
3U-R-RL
dcRLp3dt_N = dcRLp3dt_1_A_p_3 + dcRLp3dt_2_A_p_3 + dcRLp3dt_1_B_2_p_3 + dcRLp3dt_2_B_2_p_3 +\
dcRLp3dt_1_C_2_p_1_3 + dcRLp3dt_2_C_2_p_1_3 +\
dcRLp3dt_1_C_2_p_2_3 + dcRLp3dt_2_C_2_p_2_3;
![]()
Substitute (use all equations)
eq_RLp3_N__3U_R_RL:= % | eq_RLp3_Ap3_1c | eq_RLp3_Ap3_2c \
| eq_RLp3_B2p3_1c | eq_RLp3_B2p3_2c \
| eq_RLp3_C2p13_1c | eq_RLp3_C2p13_2c \
| eq_RLp3_C2p23_1c | eq_RLp3_C2p23_2c \
| eq_RLp3_C2p34_1c | eq_RLp3_C2p34_2c \
| eq_RLp3_C2p35_1c | eq_RLp3_C2p35_2c;
![]()
4U-R-RL
dcRLp3dt_N = dcRLp3dt_1_A_p_3 + dcRLp3dt_2_A_p_3 + dcRLp3dt_1_B_2_p_3 + dcRLp3dt_2_B_2_p_3 +\
dcRLp3dt_1_C_2_p_1_3 + dcRLp3dt_2_C_2_p_1_3 +\
dcRLp3dt_1_C_2_p_2_3 + dcRLp3dt_2_C_2_p_2_3+\
dcRLp3dt_1_C_2_p_3_4 + dcRLp3dt_2_C_2_p_3_4;

Substitute (use all equations)
eq_RLp3_N__4U_R_RL:= % | eq_RLp3_Ap3_1c | eq_RLp3_Ap3_2c \
| eq_RLp3_B2p3_1c | eq_RLp3_B2p3_2c \
| eq_RLp3_C2p13_1c | eq_RLp3_C2p13_2c \
| eq_RLp3_C2p23_1c | eq_RLp3_C2p23_2c \
| eq_RLp3_C2p34_1c | eq_RLp3_C2p34_2c \
| eq_RLp3_C2p35_1c | eq_RLp3_C2p35_2c;

5U-R-RL
dcRLp3dt_N = dcRLp3dt_1_A_p_3 + dcRLp3dt_2_A_p_3 + dcRLp3dt_1_B_2_p_3 + dcRLp3dt_2_B_2_p_3 +\
dcRLp3dt_1_C_2_p_1_3 + dcRLp3dt_2_C_2_p_1_3 +\
dcRLp3dt_1_C_2_p_2_3 + dcRLp3dt_2_C_2_p_2_3 +\
dcRLp3dt_1_C_2_p_3_4 + dcRLp3dt_2_C_2_p_3_4 +\
dcRLp3dt_1_C_2_p_3_5 + dcRLp3dt_2_C_2_p_3_5;

Substitute (use all equations)
eq_RLp3_N__5U_R_RL:= % | eq_RLp3_Ap3_1c | eq_RLp3_Ap3_2c \
| eq_RLp3_B2p3_1c | eq_RLp3_B2p3_2c \
| eq_RLp3_C2p13_1c | eq_RLp3_C2p13_2c \
| eq_RLp3_C2p23_1c | eq_RLp3_C2p23_2c \
| eq_RLp3_C2p34_1c | eq_RLp3_C2p34_2c \
| eq_RLp3_C2p35_1c | eq_RLp3_C2p35_2c;
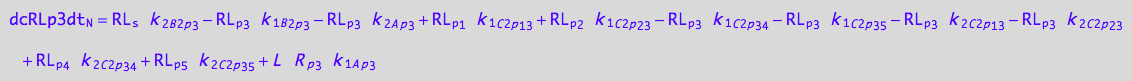
eq_RLp3_N__3U_R_RL
![]()
eq_RLp3_N__4U_R_RL

eq_RLp3_N__5U_R_RL
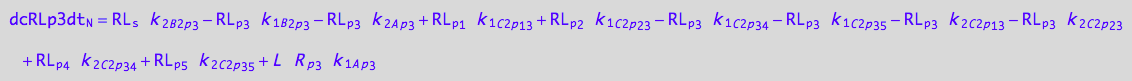
Back to Equations for each species
Equations group: RLp4
R''''+L<=>RL''''
Constants: k_1_A_p_4 (forward), k_2_A_p_4 (reverse).
NOTE: Kinetic equations for this transition were already defined!
Equations subgroup: Ap4
a forward reaction rate
eq_RLp4_Ap4_1a:= eq_Rp4_Ap4_1a
![]()
a partial conversion rate of RL'''' in this transition
molecularity:=1:
eq_RLp4_Ap4_1b:= dcRLp4dt_1_A_p_4 = molecularity*Rate_1_A_p_4
![]()
the final form
eq_RLp4_Ap4_1c:= eq_RLp4_Ap4_1b | eq_RLp4_Ap4_1a
![]()
a reverse reaction rate for the transition
eq_RLp4_Ap4_2a:= eq_Rp4_Ap4_2a
![]()
a partial conversion rate of RL'''' in this transition
molecularity:=-1:
eq_RLp4_Ap4_2b:= dcRLp4dt_2_A_p_4 = molecularity*Rate_2_A_p_4
![]()
the final form
eq_RLp4_Ap4_2c:= eq_RLp4_Ap4_2b | eq_RLp4_Ap4_2a
![]()
RL'''' <=> RL*
Constants: k_1_B_2_p_4 (forward), k_2_B_2_p_4 (reverse).
Equations subgroup: B2p4
a forward reaction rate for the transition
eq_RLp4_B2p4_1a:= Rate_1_B_2_p_4 = k_1_B_2_p_4*RL_p_4
![]()
a partial conversion rate of RL'''' in this transition
molecularity:=-1:
eq_RLp4_B2p4_1b:= dcRLp4dt_1_B_2_p_4 = molecularity*Rate_1_B_2_p_4
![]()
the final form
eq_RLp4_B2p4_1c:= eq_RLp4_B2p4_1b | eq_RLp4_B2p4_1a
![]()
a reverse reaction rate for the transition
eq_RLp4_B2p4_2a:= Rate_2_B_2_p_4 = k_2_B_2_p_4*RL_s
![]()
a partial conversion rate of RL'''' in this transition
molecularity:=1:
eq_RLp4_B2p4_2b:= dcRLp4dt_2_B_2_p_4 = molecularity*Rate_2_B_2_p_4
![]()
the final form
eq_RLp4_B2p4_2c:= eq_RLp4_B2p4_2b | eq_RLp4_B2p4_2a
![]()
RL' <=> RL''''
Constants: k_1_C_2_p_1_4 (forward), k_2_C_2_p_1_4 (reverse).
NOTE: Kinetic equations for this transition were already defined!
Equations subgroup: C2p14
a forward reaction rate for the transition
eq_RLp4_C2p14_1a:= eq_RLp1_C2p14_1a
![]()
a partial conversion rate of RL'''' in this transition
molecularity:=1:
eq_RLp4_C2p14_1b:= dcRLp4dt_1_C_2_p_1_4 = molecularity*Rate_1_C_2_p_1_4
![]()
the final form
eq_RLp4_C2p14_1c:= eq_RLp4_C2p14_1b | eq_RLp4_C2p14_1a
![]()
a reverse reaction rate for the transition
eq_RLp4_C2p14_2a:= eq_RLp1_C2p14_2a
![]()
a partial conversion rate of RL'''' in this transition
molecularity:=-1:
eq_RLp4_C2p14_2b:= dcRLp4dt_2_C_2_p_1_4 = molecularity*Rate_2_C_2_p_1_4
![]()
the final form
eq_RLp4_C2p14_2c:= eq_RLp4_C2p14_2b | eq_RLp4_C2p14_2a
![]()
RL'' <=> RL''''
Constants: k_1_C_2_p_2_4 (forward), k_2_C_2_p_2_4 (reverse).
NOTE: Kinetic equations for this transition were already defined!
Equations subgroup: C2p24
a forward reaction rate for the transition
eq_RLp4_C2p24_1a:= eq_RLp2_C2p24_1a
![]()
a partial conversion rate of RL'''' in this transition
molecularity:=1:
eq_RLp4_C2p24_1b:= dcRLp4dt_1_C_2_p_2_4 = molecularity*Rate_1_C_2_p_2_4
![]()
the final form
eq_RLp4_C2p24_1c:= eq_RLp4_C2p24_1b | eq_RLp4_C2p24_1a
![]()
a reverse reaction rate for the transition
eq_RLp4_C2p24_2a:= eq_RLp2_C2p24_2a
![]()
a partial conversion rate of RL'''' in this transition
molecularity:=-1:
eq_RLp4_C2p24_2b:= dcRLp4dt_2_C_2_p_2_4 = molecularity*Rate_2_C_2_p_2_4
![]()
the final form
eq_RLp4_C2p24_2c:= eq_RLp4_C2p24_2b | eq_RLp4_C2p24_2a
![]()
RL''' <=> RL''''
Constants: k_1_C_2_p_3_4 (forward), k_2_C_2_p_3_4 (reverse).
NOTE: Kinetic equations for this transition were already defined!
Equations subgroup: C2p34
a forward reaction rate for the transition
eq_RLp4_C2p34_1a:= eq_RLp3_C2p34_1a
![]()
a partial conversion rate of RL'''' in this transition
molecularity:=1:
eq_RLp4_C2p34_1b:= dcRLp4dt_1_C_2_p_3_4 = molecularity*Rate_1_C_2_p_3_4
![]()
the final form
eq_RLp4_C2p34_1c:= eq_RLp4_C2p34_1b | eq_RLp4_C2p34_1a
![]()
a reverse reaction rate for the transition
eq_RLp4_C2p34_2a:= eq_RLp3_C2p34_2a
![]()
a partial conversion rate of RL'''' in this transition
molecularity:=-1:
eq_RLp4_C2p34_2b:= dcRLp4dt_2_C_2_p_3_4 = molecularity*Rate_2_C_2_p_3_4
![]()
the final form
eq_RLp4_C2p34_2c:= eq_RLp4_C2p34_2b | eq_RLp4_C2p34_2a
![]()
RL'''' <=> RL'''''
Constants: k_1_C_2_p_4_5 (forward), k_2_C_2_p_4_5 (reverse).
Equations subgroup: C2p45
a forward reaction rate for the transition
eq_RLp4_C2p45_1a:= Rate_1_C_2_p_4_5 = k_1_C_2_p_4_5*RL_p_4
![]()
a partial conversion rate of RL'''' in this transition
molecularity:=-1:
eq_RLp4_C2p45_1b:= dcRLp4dt_1_C_2_p_4_5 = molecularity*Rate_1_C_2_p_4_5
![]()
the final form
eq_RLp4_C2p45_1c:= eq_RLp4_C2p45_1b | eq_RLp4_C2p45_1a
![]()
a reverse reaction rate for the transition
eq_RLp4_C2p45_2a:= Rate_2_C_2_p_4_5 = k_2_C_2_p_4_5*RL_p_5
![]()
a partial conversion rate of RL'''' in this transition
molecularity:=1:
eq_RLp4_C2p45_2b:= dcRLp4dt_2_C_2_p_4_5 = molecularity*Rate_2_C_2_p_4_5
![]()
the final form
eq_RLp4_C2p45_2c:= eq_RLp4_C2p45_2b | eq_RLp4_C2p45_2a
![]()
Summary of partial conversion rates for the species
eq_RLp4_Ap4_1c;eq_RLp4_Ap4_2c;
![]()
![]()
eq_RLp4_B2p4_1c;eq_RLp4_B2p4_2c
![]()
![]()
eq_RLp4_C2p14_1c;eq_RLp4_C2p14_2c;
eq_RLp4_C2p24_1c;eq_RLp4_C2p24_2c;
eq_RLp4_C2p34_1c;eq_RLp4_C2p34_2c;
eq_RLp4_C2p45_1c;eq_RLp4_C2p45_2c;
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Net conversion rate for the species
I will create equations for all five versions of the mechanism.
1U-R-RL, 2U-R-RL, 3U-R-RL - not needed; no RL'''' species
4U-R-RL
dcRLp4dt_N = dcRLp4dt_1_A_p_4 + dcRLp4dt_2_A_p_4 + dcRLp4dt_1_B_2_p_4 + dcRLp4dt_2_B_2_p_4 +\
dcRLp4dt_1_C_2_p_1_4 + dcRLp4dt_2_C_2_p_1_4 +\
dcRLp4dt_1_C_2_p_2_4 + dcRLp4dt_2_C_2_p_2_4 +\
dcRLp4dt_1_C_2_p_3_4 + dcRLp4dt_2_C_2_p_3_4;

Substitute (use all equations)
eq_RLp4_N__4U_R_RL:= % | eq_RLp4_Ap4_1c | eq_RLp4_Ap4_2c \
| eq_RLp4_B2p4_1c | eq_RLp4_B2p4_2c \
| eq_RLp4_C2p14_1c | eq_RLp4_C2p14_2c \
| eq_RLp4_C2p24_1c | eq_RLp4_C2p24_2c \
| eq_RLp4_C2p34_1c | eq_RLp4_C2p34_2c \
| eq_RLp4_C2p45_1c | eq_RLp4_C2p45_2c;

5U-R-RL
dcRLp4dt_N = dcRLp4dt_1_A_p_4 + dcRLp4dt_2_A_p_4 + dcRLp4dt_1_B_2_p_4 + dcRLp4dt_2_B_2_p_4 +\
dcRLp4dt_1_C_2_p_1_4 + dcRLp4dt_2_C_2_p_1_4 +\
dcRLp4dt_1_C_2_p_2_4 + dcRLp4dt_2_C_2_p_2_4 +\
dcRLp4dt_1_C_2_p_3_4 + dcRLp4dt_2_C_2_p_3_4 +\
dcRLp4dt_1_C_2_p_4_5 + dcRLp4dt_2_C_2_p_4_5;

Substitute (use all equations)
eq_RLp4_N__5U_R_RL:= % | eq_RLp4_Ap4_1c | eq_RLp4_Ap4_2c \
| eq_RLp4_B2p4_1c | eq_RLp4_B2p4_2c \
| eq_RLp4_C2p14_1c | eq_RLp4_C2p14_2c \
| eq_RLp4_C2p24_1c | eq_RLp4_C2p24_2c \
| eq_RLp4_C2p34_1c | eq_RLp4_C2p34_2c \
| eq_RLp4_C2p45_1c | eq_RLp4_C2p45_2c;
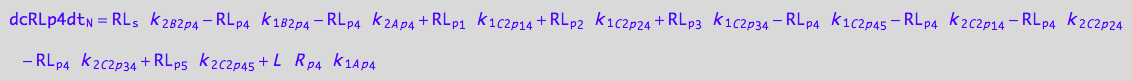
eq_RLp4_N__4U_R_RL

eq_RLp4_N__5U_R_RL
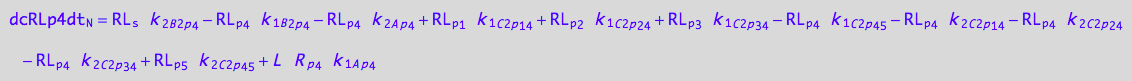
Back to Equations for each species
Equations group: RLp5
R'''''+L<=>RL'''''
Constants: k_1_A_p_5 (forward), k_2_A_p_5 (reverse).
NOTE: Kinetic equations for this transition were already defined!
Equations subgroup: Ap5
a forward reaction rate
eq_RLp5_Ap5_1a:= eq_Rp5_Ap5_1a
![]()
a partial conversion rate of RL''''' in this transition
molecularity:=1:
eq_RLp5_Ap5_1b:= dcRLp5dt_1_A_p_5 = molecularity*Rate_1_A_p_5
![]()
the final form
eq_RLp5_Ap5_1c:= eq_RLp5_Ap5_1b | eq_RLp5_Ap5_1a
![]()
a reverse reaction rate for the transition
eq_RLp5_Ap5_2a:= eq_Rp5_Ap5_2a
![]()
a partial conversion rate of RL''''' in this transition
molecularity:=-1:
eq_RLp5_Ap5_2b:= dcRLp5dt_2_A_p_5 = molecularity*Rate_2_A_p_5
![]()
the final form
eq_RLp5_Ap5_2c:= eq_RLp5_Ap5_2b | eq_RLp5_Ap5_2a
![]()
RL''''' <=> RL*
Constants: k_1_B_2_p_5 (forward), k_2_B_2_p_5 (reverse).
Equations subgroup: B2p5
a forward reaction rate for the transition
eq_RLp5_B2p5_1a:= Rate_1_B_2_p_5 = k_1_B_2_p_5*RL_p_5
![]()
a partial conversion rate of RL''''' in this transition
molecularity:=-1:
eq_RLp5_B2p5_1b:= dcRLp5dt_1_B_2_p_5 = molecularity*Rate_1_B_2_p_5
![]()
the final form
eq_RLp5_B2p5_1c:= eq_RLp5_B2p5_1b | eq_RLp5_B2p5_1a
![]()
a reverse reaction rate for the transition
eq_RLp5_B2p5_2a:= Rate_2_B_2_p_5 = k_2_B_2_p_5*RL_s
![]()
a partial conversion rate of RL''''' in this transition
molecularity:=1:
eq_RLp5_B2p5_2b:= dcRLp5dt_2_B_2_p_5 = molecularity*Rate_2_B_2_p_5
![]()
the final form
eq_RLp5_B2p5_2c:= eq_RLp5_B2p5_2b | eq_RLp5_B2p5_2a
![]()
RL' <=> RL'''''
Constants: k_1_C_2_p_1_5 (forward), k_2_C_2_p_1_5 (reverse).
NOTE: Kinetic equations for this transition were already defined!
Equations subgroup: C2p15
a forward reaction rate for the transition
eq_RLp5_C2p15_1a:= eq_RLp1_C2p15_1a
![]()
a partial conversion rate of RL''''' in this transition
molecularity:=1:
eq_RLp5_C2p15_1b:= dcRLp5dt_1_C_2_p_1_5 = molecularity*Rate_1_C_2_p_1_5
![]()
the final form
eq_RLp5_C2p15_1c:= eq_RLp5_C2p15_1b | eq_RLp5_C2p15_1a
![]()
a reverse reaction rate for the transition
eq_RLp5_C2p15_2a:= eq_RLp1_C2p15_2a
![]()
a partial conversion rate of RL''''' in this transition
molecularity:=-1:
eq_RLp5_C2p15_2b:= dcRLp5dt_2_C_2_p_1_5 = molecularity*Rate_2_C_2_p_1_5
![]()
the final form
eq_RLp5_C2p15_2c:= eq_RLp5_C2p15_2b | eq_RLp5_C2p15_2a
![]()
RL'' <=> RL'''''
Constants: k_1_C_2_p_2_5 (forward), k_2_C_2_p_2_5 (reverse).
NOTE: Kinetic equations for this transition were already defined!
Equations subgroup: C2p25
a forward reaction rate for the transition
eq_RLp5_C2p25_1a:= eq_RLp2_C2p25_1a
![]()
a partial conversion rate of RL''''' in this transition
molecularity:=1:
eq_RLp5_C2p25_1b:= dcRLp5dt_1_C_2_p_2_5 = molecularity*Rate_1_C_2_p_2_5
![]()
the final form
eq_RLp5_C2p25_1c:= eq_RLp5_C2p25_1b | eq_RLp5_C2p25_1a
![]()
a reverse reaction rate for the transition
eq_RLp5_C2p25_2a:= eq_RLp2_C2p25_2a
![]()
a partial conversion rate of RL''''' in this transition
molecularity:=-1:
eq_RLp5_C2p25_2b:= dcRLp5dt_2_C_2_p_2_5 = molecularity*Rate_2_C_2_p_2_5
![]()
the final form
eq_RLp5_C2p25_2c:= eq_RLp5_C2p25_2b | eq_RLp5_C2p25_2a
![]()
RL''' <=> RL'''''
Constants: k_1_C_2_p_3_5 (forward), k_2_C_2_p_3_5 (reverse).
NOTE: Kinetic equations for this transition were already defined!
Equations subgroup: C2p35
a forward reaction rate for the transition
eq_RLp5_C2p35_1a:= eq_RLp3_C2p35_1a
![]()
a partial conversion rate of RL''''' in this transition
molecularity:=1:
eq_RLp5_C2p35_1b:= dcRLp5dt_1_C_2_p_3_5 = molecularity*Rate_1_C_2_p_3_5
![]()
the final form
eq_RLp5_C2p35_1c:= eq_RLp5_C2p35_1b | eq_RLp5_C2p35_1a
![]()
a reverse reaction rate for the transition
eq_RLp5_C2p35_2a:= eq_RLp3_C2p35_2a
![]()
a partial conversion rate of RL''''' in this transition
molecularity:=-1:
eq_RLp5_C2p35_2b:= dcRLp5dt_2_C_2_p_3_5 = molecularity*Rate_2_C_2_p_3_5
![]()
the final form
eq_RLp5_C2p35_2c:= eq_RLp5_C2p35_2b | eq_RLp5_C2p35_2a
![]()
RL'''' <=> RL'''''
Constants: k_1_C_2_p_4_5 (forward), k_2_C_2_p_4_5 (reverse).
NOTE: Kinetic equations for this transition were already defined!
Equations subgroup: C2p45
a forward reaction rate for the transition
eq_RLp5_C2p45_1a:= eq_RLp4_C2p45_1a
![]()
a partial conversion rate of RL''''' in this transition
molecularity:=1:
eq_RLp5_C2p45_1b:= dcRLp5dt_1_C_2_p_4_5 = molecularity*Rate_1_C_2_p_4_5
![]()
the final form
eq_RLp5_C2p45_1c:= eq_RLp5_C2p45_1b | eq_RLp5_C2p45_1a
![]()
a reverse reaction rate for the transition
eq_RLp5_C2p45_2a:= eq_RLp4_C2p45_2a
![]()
a partial conversion rate of RL''''' in this transition
molecularity:=-1:
eq_RLp5_C2p45_2b:= dcRLp5dt_2_C_2_p_4_5 = molecularity*Rate_2_C_2_p_4_5
![]()
the final form
eq_RLp5_C2p45_2c:= eq_RLp5_C2p45_2b | eq_RLp5_C2p45_2a
![]()
Summary of partial conversion rates for the species
eq_RLp5_Ap5_1c;eq_RLp5_Ap5_2c;
![]()
![]()
eq_RLp5_B2p5_1c;eq_RLp5_B2p5_2c
![]()
![]()
eq_RLp5_C2p15_1c;eq_RLp5_C2p15_2c;
eq_RLp5_C2p25_1c;eq_RLp5_C2p25_2c;
eq_RLp5_C2p35_1c;eq_RLp5_C2p35_2c;
eq_RLp5_C2p45_1c;eq_RLp5_C2p45_2c;
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Net conversion rate for the species
I will create equations for all five versions of the mechanism.
1U-R-RL, 2U-R-RL, 3U-R-RL, 4U-R-RL - not needed; no RL''''' species
5U-R-RL
dcRLp5dt_N = dcRLp5dt_1_A_p_5 + dcRLp5dt_2_A_p_5 + dcRLp5dt_1_B_2_p_5 + dcRLp5dt_2_B_2_p_5 +\
dcRLp5dt_1_C_2_p_1_5 + dcRLp5dt_2_C_2_p_1_5 +\
dcRLp5dt_1_C_2_p_2_5 + dcRLp5dt_2_C_2_p_2_5 +\
dcRLp5dt_1_C_2_p_3_5 + dcRLp5dt_2_C_2_p_3_5 +\
dcRLp5dt_1_C_2_p_4_5 + dcRLp5dt_2_C_2_p_4_5;

Substitute (use all equations)
eq_RLp5_N__5U_R_RL:= % | eq_RLp5_Ap5_1c | eq_RLp5_Ap5_2c \
| eq_RLp5_B2p5_1c | eq_RLp5_B2p5_2c \
| eq_RLp5_C2p15_1c | eq_RLp5_C2p15_2c \
| eq_RLp5_C2p25_1c | eq_RLp5_C2p25_2c \
| eq_RLp5_C2p35_1c | eq_RLp5_C2p35_2c \
| eq_RLp5_C2p45_1c | eq_RLp5_C2p45_2c;
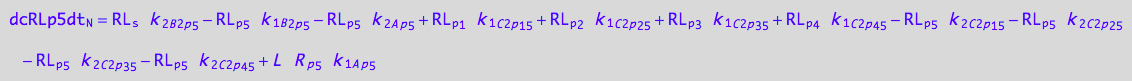
eq_RLp5_N__5U_R_RL
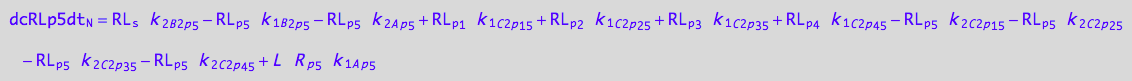
Back to Equations for each species
Equations group: Rs
R* <=> R'
Constants: k_1_B_1_p_1 (forward), k_2_B_1_p_1 (reverse).
NOTE: Kinetic equations for this transition were already defined!
Equations subgroup: B1p1
a forward reaction rate for the transition
eq_Rs_B1p1_1a:= eq_Rp1_B1p1_1a
![]()
a partial conversion rate of R* in this transition
molecularity:=-1:
eq_Rs_B1p1_1b:= dcRsdt_1_B_1_p_1 = molecularity*Rate_1_B_1_p_1
![]()
the final form
eq_Rs_B1p1_1c:= eq_Rs_B1p1_1b | eq_Rs_B1p1_1a
![]()
a reverse reaction rate for the transition
eq_Rs_B1p1_2a:= eq_Rp1_B1p1_2a
![]()
a partial conversion rate of R* in this transition
molecularity:=1:
eq_Rs_B1p1_2b:= dcRsdt_2_B_1_p_1 = molecularity*Rate_2_B_1_p_1
![]()
the final form
eq_Rs_B1p1_2c:= eq_Rs_B1p1_2b | eq_Rs_B1p1_2a
![]()
R* <=> R''
Constants: k_1_B_1_p_2 (forward), k_2_B_1_p_2 (reverse).
NOTE: Kinetic equations for this transition were already defined!
Equations subgroup: B1p2
a forward reaction rate for the transition
eq_Rs_B1p2_1a:= eq_Rp2_B1p2_1a
![]()
a partial conversion rate of R* in this transition
molecularity:=-1:
eq_Rs_B1p2_1b:= dcRsdt_1_B_1_p_2 = molecularity*Rate_1_B_1_p_2
![]()
the final form
eq_Rs_B1p2_1c:= eq_Rs_B1p2_1b | eq_Rs_B1p2_1a
![]()
a reverse reaction rate for the transition
eq_Rs_B1p2_2a:= eq_Rp2_B1p2_2a
![]()
a partial conversion rate of R* in this transition
molecularity:=1:
eq_Rs_B1p2_2b:= dcRsdt_2_B_1_p_2 = molecularity*Rate_2_B_1_p_2
![]()
the final form
eq_Rs_B1p2_2c:= eq_Rs_B1p2_2b | eq_Rs_B1p2_2a
![]()
R* <=> R'''
Constants: k_1_B_1_p_3 (forward), k_2_B_1_p_3 (reverse).
NOTE: Kinetic equations for this transition were already defined!
Equations subgroup: B1p3
a forward reaction rate for the transition
eq_Rs_B1p3_1a:= eq_Rp3_B1p3_1a
![]()
a partial conversion rate of R* in this transition
molecularity:=-1:
eq_Rs_B1p3_1b:= dcRsdt_1_B_1_p_3 = molecularity*Rate_1_B_1_p_3
![]()
the final form
eq_Rs_B1p3_1c:= eq_Rs_B1p3_1b | eq_Rs_B1p3_1a
![]()
a reverse reaction rate for the transition
eq_Rs_B1p3_2a:= eq_Rp3_B1p3_2a
![]()
a partial conversion rate of R* in this transition
molecularity:=1:
eq_Rs_B1p3_2b:= dcRsdt_2_B_1_p_3 = molecularity*Rate_2_B_1_p_3
![]()
the final form
eq_Rs_B1p3_2c:= eq_Rs_B1p3_2b | eq_Rs_B1p3_2a
![]()
R* <=> R''''
Constants: k_1_B_1_p_4 (forward), k_2_B_1_p_4 (reverse).
NOTE: Kinetic equations for this transition were already defined!
Equations subgroup: B1p4
a forward reaction rate for the transition
eq_Rs_B1p4_1a:= eq_Rp4_B1p4_1a
![]()
a partial conversion rate of R* in this transition
molecularity:=-1:
eq_Rs_B1p4_1b:= dcRsdt_1_B_1_p_4 = molecularity*Rate_1_B_1_p_4
![]()
the final form
eq_Rs_B1p4_1c:= eq_Rs_B1p4_1b | eq_Rs_B1p4_1a
![]()
a reverse reaction rate for the transition
eq_Rs_B1p4_2a:= eq_Rp4_B1p4_2a
![]()
a partial conversion rate of R* in this transition
molecularity:=1:
eq_Rs_B1p4_2b:= dcRsdt_2_B_1_p_4 = molecularity*Rate_2_B_1_p_4
![]()
the final form
eq_Rs_B1p4_2c:= eq_Rs_B1p4_2b | eq_Rs_B1p4_2a
![]()
R* <=> R'''''
Constants: k_1_B_1_p_5 (forward), k_2_B_1_p_5 (reverse).
NOTE: Kinetic equations for this transition were already defined!
Equations subgroup: B1p5
a forward reaction rate for the transition
eq_Rs_B1p5_1a:= eq_Rp5_B1p5_1a
![]()
a partial conversion rate of R* in this transition
molecularity:=-1:
eq_Rs_B1p5_1b:= dcRsdt_1_B_1_p_5 = molecularity*Rate_1_B_1_p_5
![]()
the final form
eq_Rs_B1p5_1c:= eq_Rs_B1p5_1b | eq_Rs_B1p5_1a
![]()
a reverse reaction rate for the transition
eq_Rs_B1p5_2a:= eq_Rp5_B1p5_2a
![]()
a partial conversion rate of R* in this transition
molecularity:=1:
eq_Rs_B1p5_2b:= dcRsdt_2_B_1_p_5 = molecularity*Rate_2_B_1_p_5
![]()
the final form
eq_Rs_B1p5_2c:= eq_Rs_B1p5_2b | eq_Rs_B1p5_2a
![]()
Summary of partial conversion rates for the species
eq_Rs_B1p1_1c; eq_Rs_B1p1_2c;
eq_Rs_B1p2_1c; eq_Rs_B1p2_2c;
eq_Rs_B1p3_1c; eq_Rs_B1p3_2c;
eq_Rs_B1p4_1c; eq_Rs_B1p4_2c;
eq_Rs_B1p5_1c; eq_Rs_B1p5_2c;
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Net conversion rate for the species
I will create equations for all five versions of the mechanism.
1U-R-RL
dcRsdt_N = dcRsdt_1_B_1_p_1 + dcRsdt_2_B_1_p_1 ;
![]()
Substitute (use all equations)
eq_Rs_N__1U_R_RL:= % | \
eq_Rs_B1p1_1c | eq_Rs_B1p1_2c | \
eq_Rs_B1p2_1c | eq_Rs_B1p2_2c | \
eq_Rs_B1p3_1c | eq_Rs_B1p3_2c | \
eq_Rs_B1p4_1c | eq_Rs_B1p4_2c | \
eq_Rs_B1p5_1c | eq_Rs_B1p5_2c ;
![]()
2U-R-RL
dcRsdt_N = dcRsdt_1_B_1_p_1 + dcRsdt_2_B_1_p_1 +\
dcRsdt_1_B_1_p_2 + dcRsdt_2_B_1_p_2;
![]()
Substitute (use all equations)
eq_Rs_N__2U_R_RL:= % | \
eq_Rs_B1p1_1c | eq_Rs_B1p1_2c | \
eq_Rs_B1p2_1c | eq_Rs_B1p2_2c | \
eq_Rs_B1p3_1c | eq_Rs_B1p3_2c | \
eq_Rs_B1p4_1c | eq_Rs_B1p4_2c | \
eq_Rs_B1p5_1c | eq_Rs_B1p5_2c ;
![]()
3U-R-RL
dcRsdt_N = dcRsdt_1_B_1_p_1 + dcRsdt_2_B_1_p_1 +\
dcRsdt_1_B_1_p_2 + dcRsdt_2_B_1_p_2 +\
dcRsdt_1_B_1_p_3 + dcRsdt_2_B_1_p_3;
![]()
Substitute (use all equations)
eq_Rs_N__3U_R_RL:= % | \
eq_Rs_B1p1_1c | eq_Rs_B1p1_2c | \
eq_Rs_B1p2_1c | eq_Rs_B1p2_2c | \
eq_Rs_B1p3_1c | eq_Rs_B1p3_2c | \
eq_Rs_B1p4_1c | eq_Rs_B1p4_2c | \
eq_Rs_B1p5_1c | eq_Rs_B1p5_2c ;
![]()
4U-R-RL
dcRsdt_N = dcRsdt_1_B_1_p_1 + dcRsdt_2_B_1_p_1 +\
dcRsdt_1_B_1_p_2 + dcRsdt_2_B_1_p_2 +\
dcRsdt_1_B_1_p_3 + dcRsdt_2_B_1_p_3 +\
dcRsdt_1_B_1_p_4 + dcRsdt_2_B_1_p_4;
![]()
Substitute (use all equations)
eq_Rs_N__4U_R_RL:= % | \
eq_Rs_B1p1_1c | eq_Rs_B1p1_2c | \
eq_Rs_B1p2_1c | eq_Rs_B1p2_2c | \
eq_Rs_B1p3_1c | eq_Rs_B1p3_2c | \
eq_Rs_B1p4_1c | eq_Rs_B1p4_2c | \
eq_Rs_B1p5_1c | eq_Rs_B1p5_2c ;
![]()
5U-R-RL
dcRsdt_N = dcRsdt_1_B_1_p_1 + dcRsdt_2_B_1_p_1 +\
dcRsdt_1_B_1_p_2 + dcRsdt_2_B_1_p_2 +\
dcRsdt_1_B_1_p_3 + dcRsdt_2_B_1_p_3 +\
dcRsdt_1_B_1_p_4 + dcRsdt_2_B_1_p_4 +\
dcRsdt_1_B_1_p_5 + dcRsdt_2_B_1_p_5;

Substitute (use all equations)
eq_Rs_N__5U_R_RL:= % | \
eq_Rs_B1p1_1c | eq_Rs_B1p1_2c | \
eq_Rs_B1p2_1c | eq_Rs_B1p2_2c | \
eq_Rs_B1p3_1c | eq_Rs_B1p3_2c | \
eq_Rs_B1p4_1c | eq_Rs_B1p4_2c | \
eq_Rs_B1p5_1c | eq_Rs_B1p5_2c ;
![]()
eq_Rs_N__1U_R_RL
![]()
eq_Rs_N__2U_R_RL
![]()
eq_Rs_N__3U_R_RL
![]()
eq_Rs_N__4U_R_RL
![]()
eq_Rs_N__5U_R_RL
![]()
Back to Equations for each species
Equations group: RLs
RL' <=> RL*
Constants: k_1_B_2_p_1 (forward), k_2_B_2_p_1 (reverse).
NOTE: Kinetic equations for this transition were already defined!
Equations subgroup: B2p1
a forward reaction rate for the transition
eq_RLs_B2p1_1a:= eq_RLp1_B2p1_1a
![]()
a partial conversion rate of RL* in this transition
molecularity:=1:
eq_RLs_B2p1_1b:= dcRLsdt_1_B_2_p_1 = molecularity*Rate_1_B_2_p_1
![]()
the final form
eq_RLs_B2p1_1c:= eq_RLs_B2p1_1b | eq_RLs_B2p1_1a
![]()
a reverse reaction rate for the transition
eq_RLs_B2p1_2a:= eq_RLp1_B2p1_2a
![]()
a partial conversion rate of RL* in this transition
molecularity:=-1:
eq_RLs_B2p1_2b:= dcRLsdt_2_B_2_p_1 = molecularity*Rate_2_B_2_p_1
![]()
the final form
eq_RLs_B2p1_2c:= eq_RLs_B2p1_2b | eq_RLs_B2p1_2a
![]()
RL'' <=> RL*
Constants: k_1_B_2_p_2 (forward), k_2_B_2_p_2 (reverse).
NOTE: Kinetic equations for this transition were already defined!
Equations subgroup: B2p2
a forward reaction rate for the transition
eq_RLs_B2p2_1a:= eq_RLp2_B2p2_1a
![]()
a partial conversion rate of RL* in this transition
molecularity:=1:
eq_RLs_B2p2_1b:= dcRLsdt_1_B_2_p_2 = molecularity*Rate_1_B_2_p_2
![]()
the final form
eq_RLs_B2p2_1c:= eq_RLs_B2p2_1b | eq_RLs_B2p2_1a
![]()
a reverse reaction rate for the transition
eq_RLs_B2p2_2a:= eq_RLp2_B2p2_2a
![]()
a partial conversion rate of RL* in this transition
molecularity:=-1:
eq_RLs_B2p2_2b:= dcRLsdt_2_B_2_p_2 = molecularity*Rate_2_B_2_p_2
![]()
the final form
eq_RLs_B2p2_2c:= eq_RLs_B2p2_2b | eq_RLs_B2p2_2a
![]()
RL''' <=> RL*
Constants: k_1_B_2_p_3 (forward), k_2_B_2_p_3 (reverse).
NOTE: Kinetic equations for this transition were already defined!
Equations subgroup: B2p3
a forward reaction rate for the transition
eq_RLs_B2p3_1a:= eq_RLp3_B2p3_1a
![]()
a partial conversion rate of RL* in this transition
molecularity:=1:
eq_RLs_B2p3_1b:= dcRLsdt_1_B_2_p_3 = molecularity*Rate_1_B_2_p_3
![]()
the final form
eq_RLs_B2p3_1c:= eq_RLs_B2p3_1b | eq_RLs_B2p3_1a
![]()
a reverse reaction rate for the transition
eq_RLs_B2p3_2a:= eq_RLp3_B2p3_2a
![]()
a partial conversion rate of RL* in this transition
molecularity:=-1:
eq_RLs_B2p3_2b:= dcRLsdt_2_B_2_p_3 = molecularity*Rate_2_B_2_p_3
![]()
the final form
eq_RLs_B2p3_2c:= eq_RLs_B2p3_2b | eq_RLs_B2p3_2a
![]()
RL'''' <=> RL*
Constants: k_1_B_2_p_4 (forward), k_2_B_2_p_4 (reverse).
NOTE: Kinetic equations for this transition were already defined!
Equations subgroup: B2p4
a forward reaction rate for the transition
eq_RLs_B2p4_1a:= eq_RLp4_B2p4_1a
![]()
a partial conversion rate of RL* in this transition
molecularity:=1:
eq_RLs_B2p4_1b:= dcRLsdt_1_B_2_p_4 = molecularity*Rate_1_B_2_p_4
![]()
the final form
eq_RLs_B2p4_1c:= eq_RLs_B2p4_1b | eq_RLs_B2p4_1a
![]()
a reverse reaction rate for the transition
eq_RLs_B2p4_2a:= eq_RLp4_B2p4_2a
![]()
a partial conversion rate of RL* in this transition
molecularity:=-1:
eq_RLs_B2p4_2b:= dcRLsdt_2_B_2_p_4 = molecularity*Rate_2_B_2_p_4
![]()
the final form
eq_RLs_B2p4_2c:= eq_RLs_B2p4_2b | eq_RLs_B2p4_2a
![]()
RL''''' <=> RL*
Constants: k_1_B_2_p_5 (forward), k_2_B_2_p_5 (reverse).
NOTE: Kinetic equations for this transition were already defined!
Equations subgroup: B2p5
a forward reaction rate for the transition
eq_RLs_B2p5_1a:= eq_RLp5_B2p5_1a
![]()
a partial conversion rate of RL* in this transition
molecularity:=1:
eq_RLs_B2p5_1b:= dcRLsdt_1_B_2_p_5 = molecularity*Rate_1_B_2_p_5
![]()
the final form
eq_RLs_B2p5_1c:= eq_RLs_B2p5_1b | eq_RLs_B2p5_1a
![]()
a reverse reaction rate for the transition
eq_RLs_B2p5_2a:= eq_RLp5_B2p5_2a
![]()
a partial conversion rate of RL* in this transition
molecularity:=-1:
eq_RLs_B2p5_2b:= dcRLsdt_2_B_2_p_5 = molecularity*Rate_2_B_2_p_5
![]()
the final form
eq_RLs_B2p5_2c:= eq_RLs_B2p5_2b | eq_RLs_B2p5_2a
![]()
Summary of partial conversion rates for the species
eq_RLs_B2p1_1c; eq_RLs_B2p1_2c;
eq_RLs_B2p2_1c; eq_RLs_B2p2_2c;
eq_RLs_B2p3_1c; eq_RLs_B2p3_2c;
eq_RLs_B2p4_1c; eq_RLs_B2p4_2c;
eq_RLs_B2p5_1c; eq_RLs_B2p5_2c;
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Net conversion rate for the species
I will create equations for all five versions of the mechanism.
1U-R-RL
dcRLsdt_N = dcRLsdt_1_B_2_p_1 + dcRLsdt_2_B_2_p_1;
![]()
Substitute (use all equations)
eq_RLs_N__1U_R_RL:= % | \
eq_RLs_B2p1_1c | eq_RLs_B2p1_2c | \
eq_RLs_B2p2_1c | eq_RLs_B2p2_2c | \
eq_RLs_B2p3_1c | eq_RLs_B2p3_2c | \
eq_RLs_B2p4_1c | eq_RLs_B2p4_2c | \
eq_RLs_B2p5_1c | eq_RLs_B2p5_2c ;
![]()
2U-R-RL
dcRLsdt_N = dcRLsdt_1_B_2_p_1 + dcRLsdt_2_B_2_p_1 +\
dcRLsdt_1_B_2_p_2 + dcRLsdt_2_B_2_p_2;
![]()
Substitute (use all equations)
eq_RLs_N__2U_R_RL:= % | \
eq_RLs_B2p1_1c | eq_RLs_B2p1_2c | \
eq_RLs_B2p2_1c | eq_RLs_B2p2_2c | \
eq_RLs_B2p3_1c | eq_RLs_B2p3_2c | \
eq_RLs_B2p4_1c | eq_RLs_B2p4_2c | \
eq_RLs_B2p5_1c | eq_RLs_B2p5_2c ;
![]()
3U-R-RL
dcRLsdt_N = dcRLsdt_1_B_2_p_1 + dcRLsdt_2_B_2_p_1 +\
dcRLsdt_1_B_2_p_2 + dcRLsdt_2_B_2_p_2 +\
dcRLsdt_1_B_2_p_3 + dcRLsdt_2_B_2_p_3;
![]()
Substitute (use all equations)
eq_RLs_N__3U_R_RL:= % | \
eq_RLs_B2p1_1c | eq_RLs_B2p1_2c | \
eq_RLs_B2p2_1c | eq_RLs_B2p2_2c | \
eq_RLs_B2p3_1c | eq_RLs_B2p3_2c | \
eq_RLs_B2p4_1c | eq_RLs_B2p4_2c | \
eq_RLs_B2p5_1c | eq_RLs_B2p5_2c ;
![]()
4U-R-RL
dcRLsdt_N = dcRLsdt_1_B_2_p_1 + dcRLsdt_2_B_2_p_1 +\
dcRLsdt_1_B_2_p_2 + dcRLsdt_2_B_2_p_2 +\
dcRLsdt_1_B_2_p_3 + dcRLsdt_2_B_2_p_3 +\
dcRLsdt_1_B_2_p_4 + dcRLsdt_2_B_2_p_4;
![]()
Substitute (use all equations)
eq_RLs_N__4U_R_RL:= % | \
eq_RLs_B2p1_1c | eq_RLs_B2p1_2c | \
eq_RLs_B2p2_1c | eq_RLs_B2p2_2c | \
eq_RLs_B2p3_1c | eq_RLs_B2p3_2c | \
eq_RLs_B2p4_1c | eq_RLs_B2p4_2c | \
eq_RLs_B2p5_1c | eq_RLs_B2p5_2c ;
![]()
5U-R-RL
dcRLsdt_N = dcRLsdt_1_B_2_p_1 + dcRLsdt_2_B_2_p_1 +\
dcRLsdt_1_B_2_p_2 + dcRLsdt_2_B_2_p_2 +\
dcRLsdt_1_B_2_p_3 + dcRLsdt_2_B_2_p_3 +\
dcRLsdt_1_B_2_p_4 + dcRLsdt_2_B_2_p_4 +\
dcRLsdt_1_B_2_p_5 + dcRLsdt_2_B_2_p_5;

Substitute (use all equations)
eq_RLs_N__5U_R_RL:= % | \
eq_RLs_B2p1_1c | eq_RLs_B2p1_2c | \
eq_RLs_B2p2_1c | eq_RLs_B2p2_2c | \
eq_RLs_B2p3_1c | eq_RLs_B2p3_2c | \
eq_RLs_B2p4_1c | eq_RLs_B2p4_2c | \
eq_RLs_B2p5_1c | eq_RLs_B2p5_2c ;

eq_RLs_N__1U_R_RL
![]()
eq_RLs_N__2U_R_RL
![]()
eq_RLs_N__3U_R_RL
![]()
eq_RLs_N__4U_R_RL
![]()
eq_RLs_N__5U_R_RL

Back to Equations for each species
Expression in terms of spin (monomer) concentrations
=>>> not needed here because we do not have oligomerization reactions.
Control expession of K matrix for U-1R-RL mechanism using old order of species
This is a derivation for comparison with the existing U-R-RL mechanism matrix: order of species as
R, R*, RL, RL* => R', R*, RL', RL*
Summary list of the net rate equations for the mechanism
eq_Rp1_N__1U_R_RL;
eq_RLp1_N__1U_R_RL;
eq_Rs_N__1U_R_RL;
eq_RLs_N__1U_R_RL
![]()
![]()
![]()
![]()
Assign sequential names to species
feq_1a:= R_p_1 = C1;
feq_1b:= R_s = C2;
feq_1c:= RL_p_1 = C3;
feq_1d:= RL_s = C4;
![]()
![]()
![]()
![]()
Assign the same order to net rate equations
feq_2a:= dcRp1dt_N = dC1dt;
feq_2b:= dcRsdt_N = dC2dt;
feq_2c:= dcRLp1dt_N = dC3dt;
feq_2d:= dcRLsdt_N = dC4dt;
![]()
![]()
![]()
![]()
Restate the equations in terms of new sequential species names (rename free ligand concentration too)
R'
eq_Rp1_N__1U_R_RL;
feq_3a:= % | feq_1a | feq_1b | feq_1c | feq_2a | feq_2b | feq_2c | feq_1d | feq_2d | L = Leq
![]()
![]()
R*
eq_Rs_N__1U_R_RL;
feq_3b:= % | feq_1a | feq_1b | feq_1c | feq_2a | feq_2b | feq_2c | feq_1d | feq_2d | L = Leq
![]()
![]()
RL'
eq_RLp1_N__1U_R_RL;
feq_3c:= % | feq_1a | feq_1b | feq_1c | feq_2a | feq_2b | feq_2c | feq_1d | feq_2d | L = Leq
![]()
![]()
RL*
eq_RLs_N__1U_R_RL;
feq_3d:= % | feq_1a | feq_1b | feq_1c | feq_2a | feq_2b | feq_2c | feq_1d | feq_2d | L = Leq
![]()
![]()
Prepare results for transfer to MATLAB
See Workflow for accurate extraction of the K matrix
Simple rules that allow catching mistakes in K matrix derivation:
(1) a sum of each column should be zero (so each constant must appear with both positive and negative sign), and
(2) each row has to have complete pairs of constants (i.e., if k12
appears there must be k21 in the same row with an opposite sign and so on).
K:=matrix(4,4,[
[ -k_2_B_1_p_1 -Leq*k_1_A_p_1, k_1_B_1_p_1, k_2_A_p_1, 0 ],
[ k_2_B_1_p_1, -k_1_B_1_p_1, 0, 0 ],
[ Leq*k_1_A_p_1, 0 , -k_1_B_2_p_1 -k_2_A_p_1, k_2_B_2_p_1 ],
[ 0, 0, k_1_B_2_p_1, -k_2_B_2_p_1 ]
])
![matrix([[- k_2_B_1_p_1 - Leq*k_1_A_p_1, k_1_B_1_p_1, k_2_A_p_1, 0], [k_2_B_1_p_1, -k_1_B_1_p_1, 0, 0], [Leq*k_1_A_p_1, 0, - k_2_A_p_1 - k_1_B_2_p_1, k_2_B_2_p_1], [0, 0, k_1_B_2_p_1, -k_2_B_2_p_1]])](5U_R_RL_images/math700.png)
Test the K matrix entry
Create a column vector of species concentrations
P:=matrix(4,1,[C1, C2, C3, C4])
![matrix([[C1], [C2], [C3], [C4]])](5U_R_RL_images/math701.png)
Multiply K and P:
dCdt_manual_input:= K*P
![matrix([[C3*k_2_A_p_1 + C2*k_1_B_1_p_1 - C1*(k_2_B_1_p_1 + Leq*k_1_A_p_1)], [C1*k_2_B_1_p_1 - C2*k_1_B_1_p_1], [C4*k_2_B_2_p_1 - C3*(k_2_A_p_1 + k_1_B_2_p_1) + C1*Leq*k_1_A_p_1], [C3*k_1_B_2_p_1 - C4*k_2_B_2_p_1]])](5U_R_RL_images/math702.png)
Collect right-hand-side parts of net rate equations expressed in sequential species names
dCdt_mupad:=matrix(4,1,[ rhs(feq_3a), rhs(feq_3b), rhs(feq_3c), rhs(feq_3d)])
![matrix([[C3*k_2_A_p_1 + C2*k_1_B_1_p_1 - C1*k_2_B_1_p_1 - C1*Leq*k_1_A_p_1], [C1*k_2_B_1_p_1 - C2*k_1_B_1_p_1], [C4*k_2_B_2_p_1 - C3*k_1_B_2_p_1 - C3*k_2_A_p_1 + C1*Leq*k_1_A_p_1], [C3*k_1_B_2_p_1 - C4*k_2_B_2_p_1]])](5U_R_RL_images/math703.png)
Compare derivation result to manual input
dCdt_mupad=dCdt_manual_input:
normal(%);
bool(%)
![matrix([[C3*k_2_A_p_1 + C2*k_1_B_1_p_1 - C1*k_2_B_1_p_1 - C1*Leq*k_1_A_p_1], [C1*k_2_B_1_p_1 - C2*k_1_B_1_p_1], [C4*k_2_B_2_p_1 - C3*k_1_B_2_p_1 - C3*k_2_A_p_1 + C1*Leq*k_1_A_p_1], [C3*k_1_B_2_p_1 - C4*k_2_B_2_p_1]]) = matrix([[C3*k_2_A_p_1 + C2*k_1_B_1_p_1 - C1*k_2_B_1_p_1 - C1*Leq*k_1_A_p_1], [C1*k_2_B_1_p_1 - C2*k_1_B_1_p_1], [C4*k_2_B_2_p_1 - C3*k_1_B_2_p_1 - C3*k_2_A_p_1 + C1*Leq*k_1_A_p_1], [C3*k_1_B_2_p_1 - C4*k_2_B_2_p_1]])](5U_R_RL_images/math704.png)
![]()
Compare to:
/Users/kovrigin_laptop/Documents/Workspace/Global_Analysis/IDAP/Mathematical_models/NMR_line_shape_models/U_5R_RL/U_5R_RL.mn
/Users/kovrigin_laptop/Documents/Workspace/Global_Analysis/IDAP/Mathematical_models/NMR_line_shape_models/U_R_RL/U_R_RL.mn
Conclusion:
Typed K-matrix is correct and corresponds to U-R-RL matrix derived earlier for IDAP if A2 transition is removed.
Expession of K matrix for U-1R-RL mechanism with current order of species
Order of species to allow for easy expansion of matrices:
R*, RL*, R', RL', R'', RL'', R''', RL''', R'''', RL'''', R''''', RL'''''
Summary list of the net rate equations for the mechanism
eq_Rp1_N__1U_R_RL;
eq_RLp1_N__1U_R_RL;
eq_Rs_N__1U_R_RL;
eq_RLs_N__1U_R_RL
![]()
![]()
![]()
![]()
Assign sequential names to species
feq_1a:= R_s = C1;
feq_1b:= RL_s = C2;
feq_1c:= R_p_1 = C3;
feq_1d:= RL_p_1 = C4;
![]()
![]()
![]()
![]()
Assign the same order to net rate equations
feq_2a:= dcRsdt_N = dC1dt;
feq_2b:= dcRLsdt_N = dC2dt;
feq_2c:= dcRp1dt_N = dC3dt;
feq_2d:= dcRLp1dt_N = dC4dt;
![]()
![]()
![]()
![]()
Restate the equations in terms of new sequential species names (rename free ligand concentration too)
R*
eq_Rs_N__1U_R_RL;
feq_3a:= % | feq_1a | feq_1b | feq_1c | feq_2a | feq_2b | feq_2c | feq_1d | feq_2d | L = Leq
![]()
![]()
RL*
eq_RLs_N__1U_R_RL;
feq_3b:= % | feq_1a | feq_1b | feq_1c | feq_2a | feq_2b | feq_2c | feq_1d | feq_2d | L = Leq
![]()
![]()
R'
eq_Rp1_N__1U_R_RL;
feq_3c:= % | feq_1a | feq_1b | feq_1c | feq_2a | feq_2b | feq_2c | feq_1d | feq_2d | L = Leq
![]()
![]()
RL'
eq_RLp1_N__1U_R_RL;
feq_3d:= % | feq_1a | feq_1b | feq_1c | feq_2a | feq_2b | feq_2c | feq_1d | feq_2d | L = Leq
![]()
![]()
Prepare results for transfer to MATLAB
See Workflow for accurate extraction of the K matrix
Simple rules that allow catching mistakes in K matrix derivation:
(1) a sum of each column should be zero (so each constant must appear with both positive and negative sign), and
(2) each row has to have complete pairs of constants (i.e., if k12
appears there must be k21 in the same row with an opposite sign and so on).
K:=matrix(4,4,[
[ -k_1_B_1_p_1, 0, k_2_B_1_p_1, 0 ],
[ 0, -k_2_B_2_p_1, 0, k_1_B_2_p_1 ],
[ k_1_B_1_p_1, 0, -k_2_B_1_p_1 -Leq*k_1_A_p_1, k_2_A_p_1 ],
[ 0, k_2_B_2_p_1, Leq*k_1_A_p_1, -k_1_B_2_p_1 -k_2_A_p_1 ]
])
![matrix([[-k_1_B_1_p_1, 0, k_2_B_1_p_1, 0], [0, -k_2_B_2_p_1, 0, k_1_B_2_p_1], [k_1_B_1_p_1, 0, - k_2_B_1_p_1 - Leq*k_1_A_p_1, k_2_A_p_1], [0, k_2_B_2_p_1, Leq*k_1_A_p_1, - k_2_A_p_1 - k_1_B_2_p_1]])](5U_R_RL_images/math726.png)
Test the K matrix entry
Create a column vector of species concentrations
P:=matrix(4,1,[C1, C2, C3, C4])
![matrix([[C1], [C2], [C3], [C4]])](5U_R_RL_images/math727.png)
Multiply K and P:
dCdt_manual_input:= K*P
![matrix([[C3*k_2_B_1_p_1 - C1*k_1_B_1_p_1], [C4*k_1_B_2_p_1 - C2*k_2_B_2_p_1], [C4*k_2_A_p_1 + C1*k_1_B_1_p_1 - C3*(k_2_B_1_p_1 + Leq*k_1_A_p_1)], [C2*k_2_B_2_p_1 - C4*(k_2_A_p_1 + k_1_B_2_p_1) + C3*Leq*k_1_A_p_1]])](5U_R_RL_images/math728.png)
Collect right-hand-side parts of net rate equations expressed in sequential species names
dCdt_mupad:=matrix(4,1,[ rhs(feq_3a), rhs(feq_3b), rhs(feq_3c), rhs(feq_3d)])
![matrix([[C3*k_2_B_1_p_1 - C1*k_1_B_1_p_1], [C4*k_1_B_2_p_1 - C2*k_2_B_2_p_1], [C4*k_2_A_p_1 + C1*k_1_B_1_p_1 - C3*k_2_B_1_p_1 - C3*Leq*k_1_A_p_1], [C2*k_2_B_2_p_1 - C4*k_1_B_2_p_1 - C4*k_2_A_p_1 + C3*Leq*k_1_A_p_1]])](5U_R_RL_images/math729.png)
Compare derivation result to manual input
dCdt_mupad=dCdt_manual_input:
normal(%);
bool(%)
![matrix([[C3*k_2_B_1_p_1 - C1*k_1_B_1_p_1], [C4*k_1_B_2_p_1 - C2*k_2_B_2_p_1], [C4*k_2_A_p_1 + C1*k_1_B_1_p_1 - C3*k_2_B_1_p_1 - C3*Leq*k_1_A_p_1], [C2*k_2_B_2_p_1 - C4*k_1_B_2_p_1 - C4*k_2_A_p_1 + C3*Leq*k_1_A_p_1]]) = matrix([[C3*k_2_B_1_p_1 - C1*k_1_B_1_p_1], [C4*k_1_B_2_p_1 - C2*k_2_B_2_p_1], [C4*k_2_A_p_1 + C1*k_1_B_1_p_1 - C3*k_2_B_1_p_1 - C3*Leq*k_1_A_p_1], [C2*k_2_B_2_p_1 - C4*k_1_B_2_p_1 - C4*k_2_A_p_1 + C3*Leq*k_1_A_p_1]])](5U_R_RL_images/math730.png)
![]()
Conclusion:
Typed K-matrix is correct
K matrix for the 1U-R-RL model with the new species order
K;
![matrix([[-k_1_B_1_p_1, 0, k_2_B_1_p_1, 0], [0, -k_2_B_2_p_1, 0, k_1_B_2_p_1], [k_1_B_1_p_1, 0, - k_2_B_1_p_1 - Leq*k_1_A_p_1, k_2_A_p_1], [0, k_2_B_2_p_1, Leq*k_1_A_p_1, - k_2_A_p_1 - k_1_B_2_p_1]])](5U_R_RL_images/math732.png)
Expession of K matrix for U-2R-RL mechanism
Order of species to allow for easy expansion of matrices:
R*, RL*, R', RL', R'', RL'', R''', RL''', R'''', RL'''', R''''', RL'''''
Summary list of the net rate equations for the mechanism
eq_Rs_N__2U_R_RL;
eq_RLs_N__2U_R_RL;
eq_Rp1_N__2U_R_RL;
eq_RLp1_N__2U_R_RL;
eq_Rp2_N__2U_R_RL;
eq_Rp2_N__2U_R_RL;
eq_RLp2_N__2U_R_RL;
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Assign sequential names to species
feq_1a:= R_s = C1;
feq_1b:= RL_s = C2;
feq_1c:= R_p_1 = C3;
feq_1d:= RL_p_1 = C4;
feq_1e:= R_p_2 = C5;
feq_1f:= RL_p_2 = C6;
![]()
![]()
![]()
![]()
![]()
![]()
Assign the same order to net rate equations
feq_2a:= dcRsdt_N = dC1dt;
feq_2b:= dcRLsdt_N = dC2dt;
feq_2c:= dcRp1dt_N = dC3dt;
feq_2d:= dcRLp1dt_N = dC4dt;
feq_2e:= dcRp2dt_N = dC5dt;
feq_2f:= dcRLp2dt_N = dC6dt;
![]()
![]()
![]()
![]()
![]()
![]()
Restate the equations in terms of new sequential species names (rename free ligand concentration too)
R*
eq_Rs_N__2U_R_RL;
feq_3a:= % |\
feq_1a | feq_2a | \
feq_1b | feq_2b | \
feq_1c | feq_2c | \
feq_1d | feq_2d | \
feq_1e | feq_2e | \
feq_1f | feq_2f | \
L = Leq
![]()
![]()
RL*
eq_RLs_N__2U_R_RL;
feq_3b:= % |\
feq_1a | feq_2a | \
feq_1b | feq_2b | \
feq_1c | feq_2c | \
feq_1d | feq_2d | \
feq_1e | feq_2e | \
feq_1f | feq_2f | \
L = Leq
![]()
![]()
R'
eq_Rp1_N__2U_R_RL;
feq_3c:= % |\
feq_1a | feq_2a | \
feq_1b | feq_2b | \
feq_1c | feq_2c | \
feq_1d | feq_2d | \
feq_1e | feq_2e | \
feq_1f | feq_2f | \
L = Leq
![]()
![]()
RL'
eq_RLp1_N__2U_R_RL;
feq_3d:= % |\
feq_1a | feq_2a | \
feq_1b | feq_2b | \
feq_1c | feq_2c | \
feq_1d | feq_2d | \
feq_1e | feq_2e | \
feq_1f | feq_2f | \
L = Leq
![]()
![]()
R''
eq_Rp2_N__2U_R_RL;
feq_3e:= % |\
feq_1a | feq_2a | \
feq_1b | feq_2b | \
feq_1c | feq_2c | \
feq_1d | feq_2d | \
feq_1e | feq_2e | \
feq_1f | feq_2f | \
L = Leq
![]()
![]()
RL''
eq_RLp2_N__2U_R_RL;
feq_3f:= % |\
feq_1a | feq_2a | \
feq_1b | feq_2b | \
feq_1c | feq_2c | \
feq_1d | feq_2d | \
feq_1e | feq_2e | \
feq_1f | feq_2f | \
L = Leq
![]()
![]()
Prepare results for transfer to MATLAB
See Workflow for accurate extraction of the K matrix
Simple rules that allow catching mistakes in K matrix derivation:
(1) a sum of each column should be zero (so each constant must appear with both positive and negative sign), and
(2) each row has to have complete pairs of constants (i.e., if k12
appears there must be k21 in the same row with an opposite sign and so on).
K:=matrix(6,6,[
[ -k_1_B_1_p_2 -k_1_B_1_p_1,0, k_2_B_1_p_1, 0, k_2_B_1_p_2, 0 ],
[ 0, -k_2_B_2_p_1 -k_2_B_2_p_2, 0, k_1_B_2_p_1, 0, k_1_B_2_p_2 ],
[ k_1_B_1_p_1, 0, -k_2_B_1_p_1 -k_1_C_1_p_1_2 -Leq*k_1_A_p_1, k_2_A_p_1 , k_2_C_1_p_1_2, 0 ],
[ 0, k_2_B_2_p_1, Leq*k_1_A_p_1, -k_1_B_2_p_1 -k_2_A_p_1 -k_1_C_2_p_1_2, 0, k_2_C_2_p_1_2 ],
[ k_1_B_1_p_2, 0, k_1_C_1_p_1_2, 0, -k_2_B_1_p_2 -k_2_C_1_p_1_2 -Leq*k_1_A_p_2, k_2_A_p_2 ],
[ 0, k_2_B_2_p_2, 0, k_1_C_2_p_1_2, Leq*k_1_A_p_2, -k_1_B_2_p_2 -k_2_A_p_2 -k_2_C_2_p_1_2 ]
])
![matrix([[- k_1_B_1_p_1 - k_1_B_1_p_2, 0, k_2_B_1_p_1, 0, k_2_B_1_p_2, 0], [0, - k_2_B_2_p_1 - k_2_B_2_p_2, 0, k_1_B_2_p_1, 0, k_1_B_2_p_2], [k_1_B_1_p_1, 0, - k_2_B_1_p_1 - k_1_C_1_p_1_2 - Leq*k_1_A_p_1, k_2_A_p_1, k_2_C_1_p_1_2, 0], [0, k_2_B_2_p_1, Leq*k_1_A_p_1, - k_2_A_p_1 - k_1_B_2_p_1 - k_1_C_2_p_1_2, 0, k_2_C_2_p_1_2], [k_1_B_1_p_2, 0, k_1_C_1_p_1_2, 0, - k_2_B_1_p_2 - k_2_C_1_p_1_2 - Leq*k_1_A_p_2, k_2_A_p_2], [0, k_2_B_2_p_2, 0, k_1_C_2_p_1_2, Leq*k_1_A_p_2, - k_2_A_p_2 - k_1_B_2_p_2 - k_2_C_2_p_1_2]])](5U_R_RL_images/math764.png)
Test the K matrix entry
Create a column vector of species concentrations
P:=matrix(6,1,[C1, C2, C3, C4, C5, C6])
![matrix([[C1], [C2], [C3], [C4], [C5], [C6]])](5U_R_RL_images/math765.png)
Multiply K and P:
dCdt_manual_input:= K*P
![matrix([[C3*k_2_B_1_p_1 + C5*k_2_B_1_p_2 - C1*(k_1_B_1_p_1 + k_1_B_1_p_2)], [C4*k_1_B_2_p_1 + C6*k_1_B_2_p_2 - C2*(k_2_B_2_p_1 + k_2_B_2_p_2)], [C4*k_2_A_p_1 + C1*k_1_B_1_p_1 + C5*k_2_C_1_p_1_2 - C3*(k_2_B_1_p_1 + k_1_C_1_p_1_2 + Leq*k_1_A_p_1)], [C2*k_2_B_2_p_1 + C6*k_2_C_2_p_1_2 - C4*(k_2_A_p_1 + k_1_B_2_p_1 + k_1_C_2_p_1_2) + C3*Leq*k_1_A_p_1], [C6*k_2_A_p_2 + C1*k_1_B_1_p_2 + C3*k_1_C_1_p_1_2 - C5*(k_2_B_1_p_2 + k_2_C_1_p_1_2 + Leq*k_1_A_p_2)], [C2*k_2_B_2_p_2 + C4*k_1_C_2_p_1_2 - C6*(k_2_A_p_2 + k_1_B_2_p_2 + k_2_C_2_p_1_2) + C5*Leq*k_1_A_p_2]])](5U_R_RL_images/math766.png)
Collect right-hand-side parts of net rate equations expressed in sequential species names
dCdt_mupad:=matrix(6,1,[ rhs(feq_3a), rhs(feq_3b), rhs(feq_3c), rhs(feq_3d), rhs(feq_3e), rhs(feq_3f)])
![matrix([[C3*k_2_B_1_p_1 - C1*k_1_B_1_p_2 - C1*k_1_B_1_p_1 + C5*k_2_B_1_p_2], [C4*k_1_B_2_p_1 + C6*k_1_B_2_p_2 - C2*k_2_B_2_p_1 - C2*k_2_B_2_p_2], [C4*k_2_A_p_1 + C1*k_1_B_1_p_1 - C3*k_2_B_1_p_1 - C3*k_1_C_1_p_1_2 + C5*k_2_C_1_p_1_2 - C3*Leq*k_1_A_p_1], [C2*k_2_B_2_p_1 - C4*k_1_B_2_p_1 - C4*k_2_A_p_1 - C4*k_1_C_2_p_1_2 + C6*k_2_C_2_p_1_2 + C3*Leq*k_1_A_p_1], [C6*k_2_A_p_2 + C1*k_1_B_1_p_2 - C5*k_2_B_1_p_2 + C3*k_1_C_1_p_1_2 - C5*k_2_C_1_p_1_2 - C5*Leq*k_1_A_p_2], [C2*k_2_B_2_p_2 - C6*k_1_B_2_p_2 - C6*k_2_A_p_2 + C4*k_1_C_2_p_1_2 - C6*k_2_C_2_p_1_2 + C5*Leq*k_1_A_p_2]])](5U_R_RL_images/math767.png)
Compare derivation result to manual input
dCdt_mupad=dCdt_manual_input:
normal(%);
bool(%)
![matrix([[C3*k_2_B_1_p_1 - C1*k_1_B_1_p_2 - C1*k_1_B_1_p_1 + C5*k_2_B_1_p_2], [C4*k_1_B_2_p_1 + C6*k_1_B_2_p_2 - C2*k_2_B_2_p_1 - C2*k_2_B_2_p_2], [C4*k_2_A_p_1 + C1*k_1_B_1_p_1 - C3*k_2_B_1_p_1 - C3*k_1_C_1_p_1_2 + C5*k_2_C_1_p_1_2 - C3*Leq*k_1_A_p_1], [C2*k_2_B_2_p_1 - C4*k_1_B_2_p_1 - C4*k_2_A_p_1 - C4*k_1_C_2_p_1_2 + C6*k_2_C_2_p_1_2 + C3*Leq*k_1_A_p_1], [C6*k_2_A_p_2 + C1*k_1_B_1_p_2 - C5*k_2_B_1_p_2 + C3*k_1_C_1_p_1_2 - C5*k_2_C_1_p_1_2 - C5*Leq*k_1_A_p_2], [C2*k_2_B_2_p_2 - C6*k_1_B_2_p_2 - C6*k_2_A_p_2 + C4*k_1_C_2_p_1_2 - C6*k_2_C_2_p_1_2 + C5*Leq*k_1_A_p_2]]) = matrix([[C3*k_2_B_1_p_1 - C1*k_1_B_1_p_2 - C1*k_1_B_1_p_1 + C5*k_2_B_1_p_2], [C4*k_1_B_2_p_1 + C6*k_1_B_2_p_2 - C2*k_2_B_2_p_1 - C2*k_2_B_2_p_2], [C4*k_2_A_p_1 + C1*k_1_B_1_p_1 - C3*k_2_B_1_p_1 - C3*k_1_C_1_p_1_2 + C5*k_2_C_1_p_1_2 - C3*Leq*k_1_A_p_1], [C2*k_2_B_2_p_1 - C4*k_1_B_2_p_1 - C4*k_2_A_p_1 - C4*k_1_C_2_p_1_2 + C6*k_2_C_2_p_1_2 + C3*Leq*k_1_A_p_1], [C6*k_2_A_p_2 + C1*k_1_B_1_p_2 - C5*k_2_B_1_p_2 + C3*k_1_C_1_p_1_2 - C5*k_2_C_1_p_1_2 - C5*Leq*k_1_A_p_2], [C2*k_2_B_2_p_2 - C6*k_1_B_2_p_2 - C6*k_2_A_p_2 + C4*k_1_C_2_p_1_2 - C6*k_2_C_2_p_1_2 + C5*Leq*k_1_A_p_2]])](5U_R_RL_images/math768.png)
![]()
Conclusion:
Typed K-matrix is correct
K matrix for the 2U-R-RL model
K;
![matrix([[- k_1_B_1_p_1 - k_1_B_1_p_2, 0, k_2_B_1_p_1, 0, k_2_B_1_p_2, 0], [0, - k_2_B_2_p_1 - k_2_B_2_p_2, 0, k_1_B_2_p_1, 0, k_1_B_2_p_2], [k_1_B_1_p_1, 0, - k_2_B_1_p_1 - k_1_C_1_p_1_2 - Leq*k_1_A_p_1, k_2_A_p_1, k_2_C_1_p_1_2, 0], [0, k_2_B_2_p_1, Leq*k_1_A_p_1, - k_2_A_p_1 - k_1_B_2_p_1 - k_1_C_2_p_1_2, 0, k_2_C_2_p_1_2], [k_1_B_1_p_2, 0, k_1_C_1_p_1_2, 0, - k_2_B_1_p_2 - k_2_C_1_p_1_2 - Leq*k_1_A_p_2, k_2_A_p_2], [0, k_2_B_2_p_2, 0, k_1_C_2_p_1_2, Leq*k_1_A_p_2, - k_2_A_p_2 - k_1_B_2_p_2 - k_2_C_2_p_1_2]])](5U_R_RL_images/math770.png)
Expession of K matrix for U-3R-RL mechanism
Order of species to allow for easy expansion of matrices:
R*, RL*, R', RL', R'', RL'', R''', RL''', R'''', RL'''', R''''', RL'''''
Summary list of the net rate equations for the mechanism
eq_Rs_N__3U_R_RL;
eq_RLs_N__3U_R_RL;
eq_Rp1_N__3U_R_RL;
eq_RLp1_N__3U_R_RL;
eq_Rp2_N__3U_R_RL;
eq_Rp2_N__3U_R_RL;
eq_RLp2_N__3U_R_RL;
eq_Rp3_N__3U_R_RL;
eq_RLp3_N__3U_R_RL;
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Assign sequential names to species
feq_1a:= R_s = C1;
feq_1b:= RL_s = C2;
feq_1c:= R_p_1 = C3;
feq_1d:= RL_p_1 = C4;
feq_1e:= R_p_2 = C5;
feq_1f:= RL_p_2 = C6;
feq_1g:= R_p_3 = C7;
feq_1h:= RL_p_3 = C8;
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Assign the same order to net rate equations
feq_2a:= dcRsdt_N = dC1dt;
feq_2b:= dcRLsdt_N = dC2dt;
feq_2c:= dcRp1dt_N = dC3dt;
feq_2d:= dcRLp1dt_N = dC4dt;
feq_2e:= dcRp2dt_N = dC5dt;
feq_2f:= dcRLp2dt_N = dC6dt;
feq_2g:= dcRp3dt_N = dC7dt;
feq_2h:= dcRLp3dt_N = dC8dt;
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Restate the equations in terms of new sequential species names (rename free ligand concentration too)
R*
eq_Rs_N__3U_R_RL;
feq_3a:= % |\
feq_1a | feq_2a | \
feq_1b | feq_2b | \
feq_1c | feq_2c | \
feq_1d | feq_2d | \
feq_1e | feq_2e | \
feq_1f | feq_2f | \
feq_1g | feq_2g | \
feq_1h | feq_2h | \
L = Leq
![]()
![]()
RL*
eq_RLs_N__3U_R_RL;
feq_3b:= % |\
feq_1a | feq_2a | \
feq_1b | feq_2b | \
feq_1c | feq_2c | \
feq_1d | feq_2d | \
feq_1e | feq_2e | \
feq_1f | feq_2f | \
feq_1g | feq_2g | \
feq_1h | feq_2h | \
L = Leq
![]()
![]()
R'
eq_Rp1_N__3U_R_RL;
feq_3c:= % |\
feq_1a | feq_2a | \
feq_1b | feq_2b | \
feq_1c | feq_2c | \
feq_1d | feq_2d | \
feq_1e | feq_2e | \
feq_1f | feq_2f | \
feq_1g | feq_2g | \
feq_1h | feq_2h | \
L = Leq
![]()
![]()
RL'
eq_RLp1_N__3U_R_RL;
feq_3d:= % |\
feq_1a | feq_2a | \
feq_1b | feq_2b | \
feq_1c | feq_2c | \
feq_1d | feq_2d | \
feq_1e | feq_2e | \
feq_1f | feq_2f | \
feq_1g | feq_2g | \
feq_1h | feq_2h | \
L = Leq
![]()
![]()
R''
eq_Rp2_N__3U_R_RL;
feq_3e:= % |\
feq_1a | feq_2a | \
feq_1b | feq_2b | \
feq_1c | feq_2c | \
feq_1d | feq_2d | \
feq_1e | feq_2e | \
feq_1f | feq_2f | \
feq_1g | feq_2g | \
feq_1h | feq_2h | \
L = Leq
![]()
![]()
RL''
eq_RLp2_N__3U_R_RL;
feq_3f:= % |\
feq_1a | feq_2a | \
feq_1b | feq_2b | \
feq_1c | feq_2c | \
feq_1d | feq_2d | \
feq_1e | feq_2e | \
feq_1f | feq_2f | \
feq_1g | feq_2g | \
feq_1h | feq_2h | \
L = Leq
![]()
![]()
R'''
eq_Rp3_N__3U_R_RL;
feq_3g:= % |\
feq_1a | feq_2a | \
feq_1b | feq_2b | \
feq_1c | feq_2c | \
feq_1d | feq_2d | \
feq_1e | feq_2e | \
feq_1f | feq_2f | \
feq_1g | feq_2g | \
feq_1h | feq_2h | \
L = Leq
![]()
![]()
RL'''
eq_RLp3_N__3U_R_RL;
feq_3h:= % |\
feq_1a | feq_2a | \
feq_1b | feq_2b | \
feq_1c | feq_2c | \
feq_1d | feq_2d | \
feq_1e | feq_2e | \
feq_1f | feq_2f | \
feq_1g | feq_2g | \
feq_1h | feq_2h | \
L = Leq
![]()
![]()
Prepare results for transfer to MATLAB
See Workflow for accurate extraction of the K matrix
Simple rules that allow catching mistakes in K matrix derivation:
(1) a sum of each column should be zero (so each constant must appear with both positive and negative sign), and
(2) each row has to have complete pairs of constants (i.e., if k12
appears there must be k21 in the same row with an opposite sign and so on).
K:=matrix(8,8,[
[ -k_1_B_1_p_2 -k_1_B_1_p_3 -k_1_B_1_p_1, 0, k_2_B_1_p_1, 0, +k_2_B_1_p_2, 0, +k_2_B_1_p_3, 0 ],
[ 0, -k_2_B_2_p_1 -k_2_B_2_p_2 -k_2_B_2_p_3, 0, k_1_B_2_p_1, 0, +k_1_B_2_p_2, 0, +k_1_B_2_p_3 ],
[ +k_1_B_1_p_1, 0, -k_2_B_1_p_1 -k_1_C_1_p_1_2 -k_1_C_1_p_1_3 -Leq*k_1_A_p_1, k_2_A_p_1, +k_2_C_1_p_1_2, 0, +k_2_C_1_p_1_3, 0 ],
[ 0, k_2_B_2_p_1, +Leq*k_1_A_p_1, -k_1_B_2_p_1 -k_2_A_p_1 -k_1_C_2_p_1_2 -k_1_C_2_p_1_3, 0, +k_2_C_2_p_1_2, 0, +k_2_C_2_p_1_3 ],
[ +k_1_B_1_p_2, 0,+k_1_C_1_p_1_2, 0, -k_2_B_1_p_2 -k_1_C_1_p_2_3 -k_2_C_1_p_1_2 -Leq*k_1_A_p_2, k_2_A_p_2, +k_2_C_1_p_2_3, 0 ],
[ 0, k_2_B_2_p_2, 0, +k_1_C_2_p_1_2, +Leq*k_1_A_p_2, -k_1_B_2_p_2 -k_2_A_p_2 -k_1_C_2_p_2_3 -k_2_C_2_p_1_2, 0, +k_2_C_2_p_2_3 ],
[ k_1_B_1_p_3, 0, +k_1_C_1_p_1_3, 0, +k_1_C_1_p_2_3, 0, -k_2_B_1_p_3 -k_2_C_1_p_1_3 -k_2_C_1_p_2_3 -Leq*k_1_A_p_3, k_2_A_p_3 ],
[ 0, k_2_B_2_p_3, 0, +k_1_C_2_p_1_3, 0, +k_1_C_2_p_2_3, +Leq*k_1_A_p_3, -k_1_B_2_p_3 -k_2_A_p_3 -k_2_C_2_p_1_3 -k_2_C_2_p_2_3 ]
])
![matrix([[- k_1_B_1_p_1 - k_1_B_1_p_2 - k_1_B_1_p_3, 0, k_2_B_1_p_1, 0, k_2_B_1_p_2, 0, k_2_B_1_p_3, 0], [0, - k_2_B_2_p_1 - k_2_B_2_p_2 - k_2_B_2_p_3, 0, k_1_B_2_p_1, 0, k_1_B_2_p_2, 0, k_1_B_2_p_3], [k_1_B_1_p_1, 0, - k_2_B_1_p_1 - k_1_C_1_p_1_2 - k_1_C_1_p_1_3 - Leq*k_1_A_p_1, k_2_A_p_1, k_2_C_1_p_1_2, 0, k_2_C_1_p_1_3, 0], [0, k_2_B_2_p_1, Leq*k_1_A_p_1, - k_2_A_p_1 - k_1_B_2_p_1 - k_1_C_2_p_1_2 - k_1_C_2_p_1_3, 0, k_2_C_2_p_1_2, 0, k_2_C_2_p_1_3], [k_1_B_1_p_2, 0, k_1_C_1_p_1_2, 0, - k_2_B_1_p_2 - k_1_C_1_p_2_3 - k_2_C_1_p_1_2 - Leq*k_1_A_p_2, k_2_A_p_2, k_2_C_1_p_2_3, 0], [0, k_2_B_2_p_2, 0, k_1_C_2_p_1_2, Leq*k_1_A_p_2, - k_2_A_p_2 - k_1_B_2_p_2 - k_1_C_2_p_2_3 - k_2_C_2_p_1_2, 0, k_2_C_2_p_2_3], [k_1_B_1_p_3, 0, k_1_C_1_p_1_3, 0, k_1_C_1_p_2_3, 0, - k_2_B_1_p_3 - k_2_C_1_p_1_3 - k_2_C_1_p_2_3 - Leq*k_1_A_p_3, k_2_A_p_3], [0, k_2_B_2_p_3, 0, k_1_C_2_p_1_3, 0, k_1_C_2_p_2_3, Leq*k_1_A_p_3, - k_2_A_p_3 - k_1_B_2_p_3 - k_2_C_2_p_1_3 - k_2_C_2_p_2_3]])](5U_R_RL_images/math812.png)
Test the K matrix entry
Create a column vector of species concentrations
P:=matrix(8,1,[C1, C2, C3, C4, C5, C6, C7, C8])
![matrix([[C1], [C2], [C3], [C4], [C5], [C6], [C7], [C8]])](5U_R_RL_images/math813.png)
Multiply K and P:
dCdt_manual_input:= K*P
![matrix([[C3*k_2_B_1_p_1 + C5*k_2_B_1_p_2 + C7*k_2_B_1_p_3 - C1*(k_1_B_1_p_1 + k_1_B_1_p_2 + k_1_B_1_p_3)], [C4*k_1_B_2_p_1 + C6*k_1_B_2_p_2 + C8*k_1_B_2_p_3 - C2*(k_2_B_2_p_1 + k_2_B_2_p_2 + k_2_B_2_p_3)], [C4*k_2_A_p_1 + C1*k_1_B_1_p_1 + C5*k_2_C_1_p_1_2 + C7*k_2_C_1_p_1_3 - C3*(k_2_B_1_p_1 + k_1_C_1_p_1_2 + k_1_C_1_p_1_3 + Leq*k_1_A_p_1)], [C2*k_2_B_2_p_1 + C6*k_2_C_2_p_1_2 + C8*k_2_C_2_p_1_3 - C4*(k_2_A_p_1 + k_1_B_2_p_1 + k_1_C_2_p_1_2 + k_1_C_2_p_1_3) + C3*Leq*k_1_A_p_1], [C6*k_2_A_p_2 + C1*k_1_B_1_p_2 + C3*k_1_C_1_p_1_2 + C7*k_2_C_1_p_2_3 - C5*(k_2_B_1_p_2 + k_1_C_1_p_2_3 + k_2_C_1_p_1_2 + Leq*k_1_A_p_2)], [C2*k_2_B_2_p_2 + C4*k_1_C_2_p_1_2 + C8*k_2_C_2_p_2_3 - C6*(k_2_A_p_2 + k_1_B_2_p_2 + k_1_C_2_p_2_3 + k_2_C_2_p_1_2) + C5*Leq*k_1_A_p_2], [C8*k_2_A_p_3 + C1*k_1_B_1_p_3 + C3*k_1_C_1_p_1_3 + C5*k_1_C_1_p_2_3 - C7*(k_2_B_1_p_3 + k_2_C_1_p_1_3 + k_2_C_1_p_2_3 + Leq*k_1_A_p_3)], [C2*k_2_B_2_p_3 + C4*k_1_C_2_p_1_3 + C6*k_1_C_2_p_2_3 - C8*(k_2_A_p_3 + k_1_B_2_p_3 + k_2_C_2_p_1_3 + k_2_C_2_p_2_3) + C7*Leq*k_1_A_p_3]])](5U_R_RL_images/math814.png)
Collect right-hand-side parts of net rate equations expressed in sequential species names
dCdt_mupad:=matrix(8,1,[ rhs(feq_3a), rhs(feq_3b), rhs(feq_3c), rhs(feq_3d), rhs(feq_3e), rhs(feq_3f), rhs(feq_3g), rhs(feq_3h)])
![matrix([[C3*k_2_B_1_p_1 - C1*k_1_B_1_p_2 - C1*k_1_B_1_p_3 - C1*k_1_B_1_p_1 + C5*k_2_B_1_p_2 + C7*k_2_B_1_p_3], [C4*k_1_B_2_p_1 + C6*k_1_B_2_p_2 + C8*k_1_B_2_p_3 - C2*k_2_B_2_p_1 - C2*k_2_B_2_p_2 - C2*k_2_B_2_p_3], [C4*k_2_A_p_1 + C1*k_1_B_1_p_1 - C3*k_2_B_1_p_1 - C3*k_1_C_1_p_1_2 - C3*k_1_C_1_p_1_3 + C5*k_2_C_1_p_1_2 + C7*k_2_C_1_p_1_3 - C3*Leq*k_1_A_p_1], [C2*k_2_B_2_p_1 - C4*k_1_B_2_p_1 - C4*k_2_A_p_1 - C4*k_1_C_2_p_1_2 - C4*k_1_C_2_p_1_3 + C6*k_2_C_2_p_1_2 + C8*k_2_C_2_p_1_3 + C3*Leq*k_1_A_p_1], [C6*k_2_A_p_2 + C1*k_1_B_1_p_2 - C5*k_2_B_1_p_2 + C3*k_1_C_1_p_1_2 - C5*k_1_C_1_p_2_3 - C5*k_2_C_1_p_1_2 + C7*k_2_C_1_p_2_3 - C5*Leq*k_1_A_p_2], [C2*k_2_B_2_p_2 - C6*k_1_B_2_p_2 - C6*k_2_A_p_2 + C4*k_1_C_2_p_1_2 - C6*k_1_C_2_p_2_3 - C6*k_2_C_2_p_1_2 + C8*k_2_C_2_p_2_3 + C5*Leq*k_1_A_p_2], [C8*k_2_A_p_3 + C1*k_1_B_1_p_3 - C7*k_2_B_1_p_3 + C3*k_1_C_1_p_1_3 + C5*k_1_C_1_p_2_3 - C7*k_2_C_1_p_1_3 - C7*k_2_C_1_p_2_3 - C7*Leq*k_1_A_p_3], [C2*k_2_B_2_p_3 - C8*k_1_B_2_p_3 - C8*k_2_A_p_3 + C4*k_1_C_2_p_1_3 + C6*k_1_C_2_p_2_3 - C8*k_2_C_2_p_1_3 - C8*k_2_C_2_p_2_3 + C7*Leq*k_1_A_p_3]])](5U_R_RL_images/math815.png)
Compare derivation result to manual input
dCdt_mupad=dCdt_manual_input:
normal(%);
bool(%)
![matrix([[C3*k_2_B_1_p_1 - C1*k_1_B_1_p_2 - C1*k_1_B_1_p_3 - C1*k_1_B_1_p_1 + C5*k_2_B_1_p_2 + C7*k_2_B_1_p_3], [C4*k_1_B_2_p_1 + C6*k_1_B_2_p_2 + C8*k_1_B_2_p_3 - C2*k_2_B_2_p_1 - C2*k_2_B_2_p_2 - C2*k_2_B_2_p_3], [C4*k_2_A_p_1 + C1*k_1_B_1_p_1 - C3*k_2_B_1_p_1 - C3*k_1_C_1_p_1_2 - C3*k_1_C_1_p_1_3 + C5*k_2_C_1_p_1_2 + C7*k_2_C_1_p_1_3 - C3*Leq*k_1_A_p_1], [C2*k_2_B_2_p_1 - C4*k_1_B_2_p_1 - C4*k_2_A_p_1 - C4*k_1_C_2_p_1_2 - C4*k_1_C_2_p_1_3 + C6*k_2_C_2_p_1_2 + C8*k_2_C_2_p_1_3 + C3*Leq*k_1_A_p_1], [C6*k_2_A_p_2 + C1*k_1_B_1_p_2 - C5*k_2_B_1_p_2 + C3*k_1_C_1_p_1_2 - C5*k_1_C_1_p_2_3 - C5*k_2_C_1_p_1_2 + C7*k_2_C_1_p_2_3 - C5*Leq*k_1_A_p_2], [C2*k_2_B_2_p_2 - C6*k_1_B_2_p_2 - C6*k_2_A_p_2 + C4*k_1_C_2_p_1_2 - C6*k_1_C_2_p_2_3 - C6*k_2_C_2_p_1_2 + C8*k_2_C_2_p_2_3 + C5*Leq*k_1_A_p_2], [C8*k_2_A_p_3 + C1*k_1_B_1_p_3 - C7*k_2_B_1_p_3 + C3*k_1_C_1_p_1_3 + C5*k_1_C_1_p_2_3 - C7*k_2_C_1_p_1_3 - C7*k_2_C_1_p_2_3 - C7*Leq*k_1_A_p_3], [C2*k_2_B_2_p_3 - C8*k_1_B_2_p_3 - C8*k_2_A_p_3 + C4*k_1_C_2_p_1_3 + C6*k_1_C_2_p_2_3 - C8*k_2_C_2_p_1_3 - C8*k_2_C_2_p_2_3 + C7*Leq*k_1_A_p_3]]) = matrix([[C3*k_2_B_1_p_1 - C1*k_1_B_1_p_2 - C1*k_1_B_1_p_3 - C1*k_1_B_1_p_1 + C5*k_2_B_1_p_2 + C7*k_2_B_1_p_3], [C4*k_1_B_2_p_1 + C6*k_1_B_2_p_2 + C8*k_1_B_2_p_3 - C2*k_2_B_2_p_1 - C2*k_2_B_2_p_2 - C2*k_2_B_2_p_3], [C4*k_2_A_p_1 + C1*k_1_B_1_p_1 - C3*k_2_B_1_p_1 - C3*k_1_C_1_p_1_2 - C3*k_1_C_1_p_1_3 + C5*k_2_C_1_p_1_2 + C7*k_2_C_1_p_1_3 - C3*Leq*k_1_A_p_1], [C2*k_2_B_2_p_1 - C4*k_1_B_2_p_1 - C4*k_2_A_p_1 - C4*k_1_C_2_p_1_2 - C4*k_1_C_2_p_1_3 + C6*k_2_C_2_p_1_2 + C8*k_2_C_2_p_1_3 + C3*Leq*k_1_A_p_1], [C6*k_2_A_p_2 + C1*k_1_B_1_p_2 - C5*k_2_B_1_p_2 + C3*k_1_C_1_p_1_2 - C5*k_1_C_1_p_2_3 - C5*k_2_C_1_p_1_2 + C7*k_2_C_1_p_2_3 - C5*Leq*k_1_A_p_2], [C2*k_2_B_2_p_2 - C6*k_1_B_2_p_2 - C6*k_2_A_p_2 + C4*k_1_C_2_p_1_2 - C6*k_1_C_2_p_2_3 - C6*k_2_C_2_p_1_2 + C8*k_2_C_2_p_2_3 + C5*Leq*k_1_A_p_2], [C8*k_2_A_p_3 + C1*k_1_B_1_p_3 - C7*k_2_B_1_p_3 + C3*k_1_C_1_p_1_3 + C5*k_1_C_1_p_2_3 - C7*k_2_C_1_p_1_3 - C7*k_2_C_1_p_2_3 - C7*Leq*k_1_A_p_3], [C2*k_2_B_2_p_3 - C8*k_1_B_2_p_3 - C8*k_2_A_p_3 + C4*k_1_C_2_p_1_3 + C6*k_1_C_2_p_2_3 - C8*k_2_C_2_p_1_3 - C8*k_2_C_2_p_2_3 + C7*Leq*k_1_A_p_3]])](5U_R_RL_images/math816.png)
![]()
Conclusion:
Typed K-matrix is correct
K matrix for the 3U-R-RL model
K;
![matrix([[- k_1_B_1_p_1 - k_1_B_1_p_2 - k_1_B_1_p_3, 0, k_2_B_1_p_1, 0, k_2_B_1_p_2, 0, k_2_B_1_p_3, 0], [0, - k_2_B_2_p_1 - k_2_B_2_p_2 - k_2_B_2_p_3, 0, k_1_B_2_p_1, 0, k_1_B_2_p_2, 0, k_1_B_2_p_3], [k_1_B_1_p_1, 0, - k_2_B_1_p_1 - k_1_C_1_p_1_2 - k_1_C_1_p_1_3 - Leq*k_1_A_p_1, k_2_A_p_1, k_2_C_1_p_1_2, 0, k_2_C_1_p_1_3, 0], [0, k_2_B_2_p_1, Leq*k_1_A_p_1, - k_2_A_p_1 - k_1_B_2_p_1 - k_1_C_2_p_1_2 - k_1_C_2_p_1_3, 0, k_2_C_2_p_1_2, 0, k_2_C_2_p_1_3], [k_1_B_1_p_2, 0, k_1_C_1_p_1_2, 0, - k_2_B_1_p_2 - k_1_C_1_p_2_3 - k_2_C_1_p_1_2 - Leq*k_1_A_p_2, k_2_A_p_2, k_2_C_1_p_2_3, 0], [0, k_2_B_2_p_2, 0, k_1_C_2_p_1_2, Leq*k_1_A_p_2, - k_2_A_p_2 - k_1_B_2_p_2 - k_1_C_2_p_2_3 - k_2_C_2_p_1_2, 0, k_2_C_2_p_2_3], [k_1_B_1_p_3, 0, k_1_C_1_p_1_3, 0, k_1_C_1_p_2_3, 0, - k_2_B_1_p_3 - k_2_C_1_p_1_3 - k_2_C_1_p_2_3 - Leq*k_1_A_p_3, k_2_A_p_3], [0, k_2_B_2_p_3, 0, k_1_C_2_p_1_3, 0, k_1_C_2_p_2_3, Leq*k_1_A_p_3, - k_2_A_p_3 - k_1_B_2_p_3 - k_2_C_2_p_1_3 - k_2_C_2_p_2_3]])](5U_R_RL_images/math818.png)
Expession of K matrix for U-4R-RL mechanism
Order of species to allow for easy expansion of matrices:
R*, RL*, R', RL', R'', RL'', R''', RL''', R'''', RL'''', R''''', RL'''''
Summary list of the net rate equations for the mechanism
eq_Rs_N__4U_R_RL;
eq_RLs_N__4U_R_RL;
eq_Rp1_N__4U_R_RL;
eq_RLp1_N__4U_R_RL;
eq_Rp2_N__4U_R_RL;
eq_Rp2_N__4U_R_RL;
eq_RLp2_N__4U_R_RL;
eq_Rp3_N__4U_R_RL;
eq_RLp3_N__4U_R_RL;
eq_Rp4_N__4U_R_RL;
eq_RLp4_N__4U_R_RL;
![]()
![]()
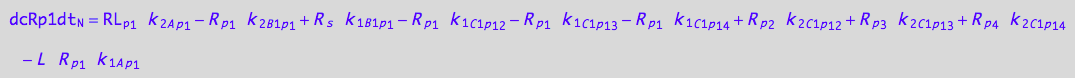

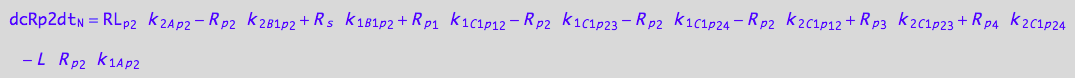
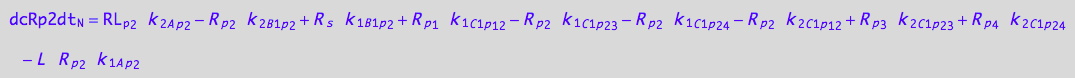

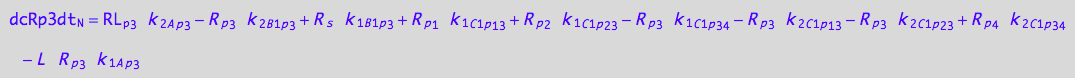

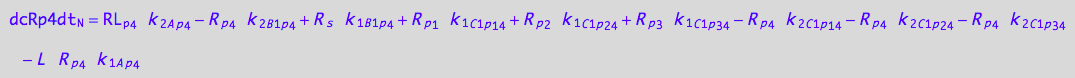

Assign sequential names to species
feq_1a:= R_s = C1;
feq_1b:= RL_s = C2;
feq_1c:= R_p_1 = C3;
feq_1d:= RL_p_1 = C4;
feq_1e:= R_p_2 = C5;
feq_1f:= RL_p_2 = C6;
feq_1g:= R_p_3 = C7;
feq_1h:= RL_p_3 = C8;
feq_1i:= R_p_4 = C9;
feq_1j:= RL_p_4 = C10;
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Assign the same order to net rate equations
feq_2a:= dcRsdt_N = dC1dt;
feq_2b:= dcRLsdt_N = dC2dt;
feq_2c:= dcRp1dt_N = dC3dt;
feq_2d:= dcRLp1dt_N = dC4dt;
feq_2e:= dcRp2dt_N = dC5dt;
feq_2f:= dcRLp2dt_N = dC6dt;
feq_2g:= dcRp3dt_N = dC7dt;
feq_2h:= dcRLp3dt_N = dC8dt;
feq_2i:= dcRp4dt_N = dC9dt;
feq_2j:= dcRLp4dt_N = dC10dt;
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Restate the equations in terms of new sequential species names (rename free ligand concentration too)
R*
eq_Rs_N__4U_R_RL;
feq_3a:= % |\
feq_1a | feq_2a | \
feq_1b | feq_2b | \
feq_1c | feq_2c | \
feq_1d | feq_2d | \
feq_1e | feq_2e | \
feq_1f | feq_2f | \
feq_1g | feq_2g | \
feq_1h | feq_2h | \
feq_1i | feq_2i | \
feq_1j | feq_2j | \
L = Leq
![]()
![]()
RL*
eq_RLs_N__4U_R_RL;
feq_3b:= % |\
feq_1a | feq_2a | \
feq_1b | feq_2b | \
feq_1c | feq_2c | \
feq_1d | feq_2d | \
feq_1e | feq_2e | \
feq_1f | feq_2f | \
feq_1g | feq_2g | \
feq_1h | feq_2h | \
feq_1i | feq_2i | \
feq_1j | feq_2j | \
L = Leq
![]()
![]()
R'
eq_Rp1_N__4U_R_RL;
feq_3c:= % |\
feq_1a | feq_2a | \
feq_1b | feq_2b | \
feq_1c | feq_2c | \
feq_1d | feq_2d | \
feq_1e | feq_2e | \
feq_1f | feq_2f | \
feq_1g | feq_2g | \
feq_1h | feq_2h | \
feq_1i | feq_2i | \
feq_1j | feq_2j | \
L = Leq
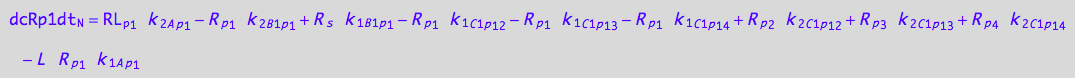
![]()
RL'
eq_RLp1_N__4U_R_RL;
feq_3d:= % |\
feq_1a | feq_2a | \
feq_1b | feq_2b | \
feq_1c | feq_2c | \
feq_1d | feq_2d | \
feq_1e | feq_2e | \
feq_1f | feq_2f | \
feq_1g | feq_2g | \
feq_1h | feq_2h | \
feq_1i | feq_2i | \
feq_1j | feq_2j | \
L = Leq

![]()
R''
eq_Rp2_N__4U_R_RL;
feq_3e:= % |\
feq_1a | feq_2a | \
feq_1b | feq_2b | \
feq_1c | feq_2c | \
feq_1d | feq_2d | \
feq_1e | feq_2e | \
feq_1f | feq_2f | \
feq_1g | feq_2g | \
feq_1h | feq_2h | \
feq_1i | feq_2i | \
feq_1j | feq_2j | \
L = Leq
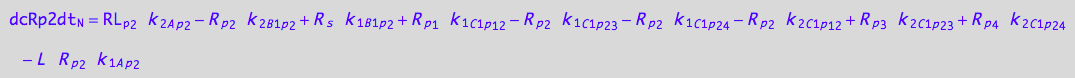
![]()
RL''
eq_RLp2_N__4U_R_RL;
feq_3f:= % |\
feq_1a | feq_2a | \
feq_1b | feq_2b | \
feq_1c | feq_2c | \
feq_1d | feq_2d | \
feq_1e | feq_2e | \
feq_1f | feq_2f | \
feq_1g | feq_2g | \
feq_1h | feq_2h | \
feq_1i | feq_2i | \
feq_1j | feq_2j | \
L = Leq

![]()
R'''
eq_Rp3_N__4U_R_RL;
feq_3g:= % |\
feq_1a | feq_2a | \
feq_1b | feq_2b | \
feq_1c | feq_2c | \
feq_1d | feq_2d | \
feq_1e | feq_2e | \
feq_1f | feq_2f | \
feq_1g | feq_2g | \
feq_1h | feq_2h | \
feq_1i | feq_2i | \
feq_1j | feq_2j | \
L = Leq
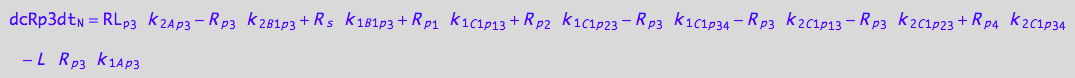
![]()
RL'''
eq_RLp3_N__4U_R_RL;
feq_3h:= % |\
feq_1a | feq_2a | \
feq_1b | feq_2b | \
feq_1c | feq_2c | \
feq_1d | feq_2d | \
feq_1e | feq_2e | \
feq_1f | feq_2f | \
feq_1g | feq_2g | \
feq_1h | feq_2h | \
feq_1i | feq_2i | \
feq_1j | feq_2j | \
L = Leq

![]()
R''''
eq_Rp4_N__4U_R_RL;
feq_3i:= % |\
feq_1a | feq_2a | \
feq_1b | feq_2b | \
feq_1c | feq_2c | \
feq_1d | feq_2d | \
feq_1e | feq_2e | \
feq_1f | feq_2f | \
feq_1g | feq_2g | \
feq_1h | feq_2h | \
feq_1i | feq_2i | \
feq_1j | feq_2j | \
L = Leq
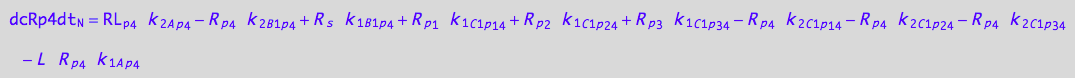
![]()
RL''''
eq_RLp4_N__4U_R_RL;
feq_3j:= % |\
feq_1a | feq_2a | \
feq_1b | feq_2b | \
feq_1c | feq_2c | \
feq_1d | feq_2d | \
feq_1e | feq_2e | \
feq_1f | feq_2f | \
feq_1g | feq_2g | \
feq_1h | feq_2h | \
feq_1i | feq_2i | \
feq_1j | feq_2j | \
L = Leq

![]()
Prepare results for transfer to MATLAB
See Workflow for accurate extraction of the K matrix
Simple rules that allow catching mistakes in K matrix derivation:
(1) a sum of each column should be zero (so each constant must appear with both positive and negative sign), and
(2) each row has to have complete pairs of constants (i.e., if k12
appears there must be k21 in the same row with an opposite sign and so on).
K:=matrix(10,10,[
[ -k_1_B_1_p_2 -k_1_B_1_p_3 -k_1_B_1_p_4 -k_1_B_1_p_1, 0, k_2_B_1_p_1, 0, +k_2_B_1_p_2, 0, +k_2_B_1_p_3, 0, +k_2_B_1_p_4 ,0 ],
[ 0, -k_2_B_2_p_1 -k_2_B_2_p_2 -k_2_B_2_p_3 -k_2_B_2_p_4, 0, k_1_B_2_p_1, 0, +k_1_B_2_p_2, 0, +k_1_B_2_p_3, 0, +k_1_B_2_p_4 ],
[ +k_1_B_1_p_1, 0, -k_2_B_1_p_1 -k_1_C_1_p_1_2 -k_1_C_1_p_1_3 -k_1_C_1_p_1_4 -Leq*k_1_A_p_1, k_2_A_p_1, +k_2_C_1_p_1_2, 0, +k_2_C_1_p_1_3,0, +k_2_C_1_p_1_4,0 ],
[ 0, k_2_B_2_p_1, +Leq*k_1_A_p_1, -k_1_B_2_p_1 -k_2_A_p_1 -k_1_C_2_p_1_2 -k_1_C_2_p_1_3 -k_1_C_2_p_1_4, 0, +k_2_C_2_p_1_2, 0, +k_2_C_2_p_1_3, 0, +k_2_C_2_p_1_4 ],
[ +k_1_B_1_p_2, 0, +k_1_C_1_p_1_2, 0, -k_2_B_1_p_2 -k_1_C_1_p_2_3 -k_1_C_1_p_2_4 -k_2_C_1_p_1_2 -Leq*k_1_A_p_2, k_2_A_p_2, +k_2_C_1_p_2_3, 0, +k_2_C_1_p_2_4,0 ],
[ 0, k_2_B_2_p_2, 0, +k_1_C_2_p_1_2, +Leq*k_1_A_p_2, -k_1_B_2_p_2 -k_2_A_p_2 -k_1_C_2_p_2_3 -k_1_C_2_p_2_4 -k_2_C_2_p_1_2, 0, +k_2_C_2_p_2_3, 0, +k_2_C_2_p_2_4 ],
[ +k_1_B_1_p_3, 0, +k_1_C_1_p_1_3, 0, +k_1_C_1_p_2_3, 0, -k_2_B_1_p_3 -k_1_C_1_p_3_4 -k_2_C_1_p_1_3 -k_2_C_1_p_2_3 -Leq*k_1_A_p_3, k_2_A_p_3, +k_2_C_1_p_3_4, 0 ],
[ 0, k_2_B_2_p_3, 0, +k_1_C_2_p_1_3, 0, +k_1_C_2_p_2_3, +Leq*k_1_A_p_3, -k_1_B_2_p_3 -k_2_A_p_3 -k_1_C_2_p_3_4 -k_2_C_2_p_1_3 -k_2_C_2_p_2_3, 0, +k_2_C_2_p_3_4 ],
[ +k_1_B_1_p_4, 0, +k_1_C_1_p_1_4, 0, +k_1_C_1_p_2_4, 0, +k_1_C_1_p_3_4, 0, -k_2_B_1_p_4 -k_2_C_1_p_1_4 -k_2_C_1_p_2_4 -k_2_C_1_p_3_4 -Leq*k_1_A_p_4, k_2_A_p_4 ],
[ 0, k_2_B_2_p_4, 0, +k_1_C_2_p_1_4, 0, +k_1_C_2_p_2_4, 0, +k_1_C_2_p_3_4, +Leq*k_1_A_p_4, -k_1_B_2_p_4 -k_2_A_p_4 -k_2_C_2_p_1_4 -k_2_C_2_p_2_4 -k_2_C_2_p_3_4 ]
])
![matrix([[- k_1_B_1_p_1 - k_1_B_1_p_2 - k_1_B_1_p_3 - k_1_B_1_p_4, 0, k_2_B_1_p_1, 0, k_2_B_1_p_2, 0, k_2_B_1_p_3, 0, k_2_B_1_p_4, 0], [0, - k_2_B_2_p_1 - k_2_B_2_p_2 - k_2_B_2_p_3 - k_2_B_2_p_4, 0, k_1_B_2_p_1, 0, k_1_B_2_p_2, 0, k_1_B_2_p_3, 0, k_1_B_2_p_4], [k_1_B_1_p_1, 0, - k_2_B_1_p_1 - k_1_C_1_p_1_2 - k_1_C_1_p_1_3 - k_1_C_1_p_1_4 - Leq*k_1_A_p_1, k_2_A_p_1, k_2_C_1_p_1_2, 0, k_2_C_1_p_1_3, 0, k_2_C_1_p_1_4, 0], [0, k_2_B_2_p_1, Leq*k_1_A_p_1, - k_2_A_p_1 - k_1_B_2_p_1 - k_1_C_2_p_1_2 - k_1_C_2_p_1_3 - k_1_C_2_p_1_4, 0, k_2_C_2_p_1_2, 0, k_2_C_2_p_1_3, 0, k_2_C_2_p_1_4], [k_1_B_1_p_2, 0, k_1_C_1_p_1_2, 0, - k_2_B_1_p_2 - k_1_C_1_p_2_3 - k_1_C_1_p_2_4 - k_2_C_1_p_1_2 - Leq*k_1_A_p_2, k_2_A_p_2, k_2_C_1_p_2_3, 0, k_2_C_1_p_2_4, 0], [0, k_2_B_2_p_2, 0, k_1_C_2_p_1_2, Leq*k_1_A_p_2, - k_2_A_p_2 - k_1_B_2_p_2 - k_1_C_2_p_2_3 - k_1_C_2_p_2_4 - k_2_C_2_p_1_2, 0, k_2_C_2_p_2_3, 0, k_2_C_2_p_2_4], [k_1_B_1_p_3, 0, k_1_C_1_p_1_3, 0, k_1_C_1_p_2_3, 0, - k_2_B_1_p_3 - k_1_C_1_p_3_4 - k_2_C_1_p_1_3 - k_2_C_1_p_2_3 - Leq*k_1_A_p_3, k_2_A_p_3, k_2_C_1_p_3_4, 0], [0, k_2_B_2_p_3, 0, k_1_C_2_p_1_3, 0, k_1_C_2_p_2_3, Leq*k_1_A_p_3, - k_2_A_p_3 - k_1_B_2_p_3 - k_1_C_2_p_3_4 - k_2_C_2_p_1_3 - k_2_C_2_p_2_3, 0, k_2_C_2_p_3_4], [k_1_B_1_p_4, 0, k_1_C_1_p_1_4, 0, k_1_C_1_p_2_4, 0, k_1_C_1_p_3_4, 0, - k_2_B_1_p_4 - k_2_C_1_p_1_4 - k_2_C_1_p_2_4 - k_2_C_1_p_3_4 - Leq*k_1_A_p_4, k_2_A_p_4], [0, k_2_B_2_p_4, 0, k_1_C_2_p_1_4, 0, k_1_C_2_p_2_4, 0, k_1_C_2_p_3_4, Leq*k_1_A_p_4, - k_2_A_p_4 - k_1_B_2_p_4 - k_2_C_2_p_1_4 - k_2_C_2_p_2_4 - k_2_C_2_p_3_4]])](5U_R_RL_images/math870.png)
Test the K matrix entry
Create a column vector of species concentrations
P:=matrix(10,1,[C1, C2, C3, C4, C5, C6, C7, C8, C9, C10])
![matrix([[C1], [C2], [C3], [C4], [C5], [C6], [C7], [C8], [C9], [C10]])](5U_R_RL_images/math871.png)
Multiply K and P:
dCdt_manual_input:= K*P
![matrix([[C3*k_2_B_1_p_1 + C5*k_2_B_1_p_2 + C7*k_2_B_1_p_3 + C9*k_2_B_1_p_4 - C1*(k_1_B_1_p_1 + k_1_B_1_p_2 + k_1_B_1_p_3 + k_1_B_1_p_4)], [C4*k_1_B_2_p_1 + C6*k_1_B_2_p_2 + C8*k_1_B_2_p_3 + C10*k_1_B_2_p_4 - C2*(k_2_B_2_p_1 + k_2_B_2_p_2 + k_2_B_2_p_3 + k_2_B_2_p_4)], [C4*k_2_A_p_1 + C1*k_1_B_1_p_1 + C5*k_2_C_1_p_1_2 + C7*k_2_C_1_p_1_3 + C9*k_2_C_1_p_1_4 - C3*(k_2_B_1_p_1 + k_1_C_1_p_1_2 + k_1_C_1_p_1_3 + k_1_C_1_p_1_4 + Leq*k_1_A_p_1)], [C2*k_2_B_2_p_1 + C6*k_2_C_2_p_1_2 + C8*k_2_C_2_p_1_3 + C10*k_2_C_2_p_1_4 - C4*(k_2_A_p_1 + k_1_B_2_p_1 + k_1_C_2_p_1_2 + k_1_C_2_p_1_3 + k_1_C_2_p_1_4) + C3*Leq*k_1_A_p_1], [C6*k_2_A_p_2 + C1*k_1_B_1_p_2 + C3*k_1_C_1_p_1_2 + C7*k_2_C_1_p_2_3 + C9*k_2_C_1_p_2_4 - C5*(k_2_B_1_p_2 + k_1_C_1_p_2_3 + k_1_C_1_p_2_4 + k_2_C_1_p_1_2 + Leq*k_1_A_p_2)], [C2*k_2_B_2_p_2 + C4*k_1_C_2_p_1_2 + C8*k_2_C_2_p_2_3 + C10*k_2_C_2_p_2_4 - C6*(k_2_A_p_2 + k_1_B_2_p_2 + k_1_C_2_p_2_3 + k_1_C_2_p_2_4 + k_2_C_2_p_1_2) + C5*Leq*k_1_A_p_2], [C8*k_2_A_p_3 + C1*k_1_B_1_p_3 + C3*k_1_C_1_p_1_3 + C5*k_1_C_1_p_2_3 + C9*k_2_C_1_p_3_4 - C7*(k_2_B_1_p_3 + k_1_C_1_p_3_4 + k_2_C_1_p_1_3 + k_2_C_1_p_2_3 + Leq*k_1_A_p_3)], [C2*k_2_B_2_p_3 + C4*k_1_C_2_p_1_3 + C6*k_1_C_2_p_2_3 + C10*k_2_C_2_p_3_4 - C8*(k_2_A_p_3 + k_1_B_2_p_3 + k_1_C_2_p_3_4 + k_2_C_2_p_1_3 + k_2_C_2_p_2_3) + C7*Leq*k_1_A_p_3], [C10*k_2_A_p_4 + C1*k_1_B_1_p_4 + C3*k_1_C_1_p_1_4 + C5*k_1_C_1_p_2_4 + C7*k_1_C_1_p_3_4 - C9*(k_2_B_1_p_4 + k_2_C_1_p_1_4 + k_2_C_1_p_2_4 + k_2_C_1_p_3_4 + Leq*k_1_A_p_4)], [C2*k_2_B_2_p_4 + C4*k_1_C_2_p_1_4 + C6*k_1_C_2_p_2_4 + C8*k_1_C_2_p_3_4 - C10*(k_2_A_p_4 + k_1_B_2_p_4 + k_2_C_2_p_1_4 + k_2_C_2_p_2_4 + k_2_C_2_p_3_4) + C9*Leq*k_1_A_p_4]])](5U_R_RL_images/math872.png)
Collect right-hand-side parts of net rate equations expressed in sequential species names
dCdt_mupad:=matrix(10,1,[ rhs(feq_3a), rhs(feq_3b), rhs(feq_3c), rhs(feq_3d), rhs(feq_3e), rhs(feq_3f), rhs(feq_3g), rhs(feq_3h), rhs(feq_3i), rhs(feq_3j)])
![matrix([[C3*k_2_B_1_p_1 - C1*k_1_B_1_p_2 - C1*k_1_B_1_p_3 - C1*k_1_B_1_p_4 - C1*k_1_B_1_p_1 + C5*k_2_B_1_p_2 + C7*k_2_B_1_p_3 + C9*k_2_B_1_p_4], [C4*k_1_B_2_p_1 + C6*k_1_B_2_p_2 + C8*k_1_B_2_p_3 + C10*k_1_B_2_p_4 - C2*k_2_B_2_p_1 - C2*k_2_B_2_p_2 - C2*k_2_B_2_p_3 - C2*k_2_B_2_p_4], [C4*k_2_A_p_1 + C1*k_1_B_1_p_1 - C3*k_2_B_1_p_1 - C3*k_1_C_1_p_1_2 - C3*k_1_C_1_p_1_3 - C3*k_1_C_1_p_1_4 + C5*k_2_C_1_p_1_2 + C7*k_2_C_1_p_1_3 + C9*k_2_C_1_p_1_4 - C3*Leq*k_1_A_p_1], [C2*k_2_B_2_p_1 - C4*k_1_B_2_p_1 - C4*k_2_A_p_1 - C4*k_1_C_2_p_1_2 - C4*k_1_C_2_p_1_3 - C4*k_1_C_2_p_1_4 + C6*k_2_C_2_p_1_2 + C8*k_2_C_2_p_1_3 + C10*k_2_C_2_p_1_4 + C3*Leq*k_1_A_p_1], [C6*k_2_A_p_2 + C1*k_1_B_1_p_2 - C5*k_2_B_1_p_2 + C3*k_1_C_1_p_1_2 - C5*k_1_C_1_p_2_3 - C5*k_1_C_1_p_2_4 - C5*k_2_C_1_p_1_2 + C7*k_2_C_1_p_2_3 + C9*k_2_C_1_p_2_4 - C5*Leq*k_1_A_p_2], [C2*k_2_B_2_p_2 - C6*k_1_B_2_p_2 - C6*k_2_A_p_2 + C4*k_1_C_2_p_1_2 - C6*k_1_C_2_p_2_3 - C6*k_1_C_2_p_2_4 - C6*k_2_C_2_p_1_2 + C8*k_2_C_2_p_2_3 + C10*k_2_C_2_p_2_4 + C5*Leq*k_1_A_p_2], [C8*k_2_A_p_3 + C1*k_1_B_1_p_3 - C7*k_2_B_1_p_3 + C3*k_1_C_1_p_1_3 + C5*k_1_C_1_p_2_3 - C7*k_1_C_1_p_3_4 - C7*k_2_C_1_p_1_3 - C7*k_2_C_1_p_2_3 + C9*k_2_C_1_p_3_4 - C7*Leq*k_1_A_p_3], [C2*k_2_B_2_p_3 - C8*k_1_B_2_p_3 - C8*k_2_A_p_3 + C4*k_1_C_2_p_1_3 + C6*k_1_C_2_p_2_3 - C8*k_1_C_2_p_3_4 - C8*k_2_C_2_p_1_3 - C8*k_2_C_2_p_2_3 + C10*k_2_C_2_p_3_4 + C7*Leq*k_1_A_p_3], [C10*k_2_A_p_4 + C1*k_1_B_1_p_4 - C9*k_2_B_1_p_4 + C3*k_1_C_1_p_1_4 + C5*k_1_C_1_p_2_4 + C7*k_1_C_1_p_3_4 - C9*k_2_C_1_p_1_4 - C9*k_2_C_1_p_2_4 - C9*k_2_C_1_p_3_4 - C9*Leq*k_1_A_p_4], [C2*k_2_B_2_p_4 - C10*k_1_B_2_p_4 - C10*k_2_A_p_4 + C4*k_1_C_2_p_1_4 + C6*k_1_C_2_p_2_4 + C8*k_1_C_2_p_3_4 - C10*k_2_C_2_p_1_4 - C10*k_2_C_2_p_2_4 - C10*k_2_C_2_p_3_4 + C9*Leq*k_1_A_p_4]])](5U_R_RL_images/math873.png)
Compare derivation result to manual input
dCdt_mupad=dCdt_manual_input:
normal(%);
bool(%)
![matrix([[C3*k_2_B_1_p_1 - C1*k_1_B_1_p_2 - C1*k_1_B_1_p_3 - C1*k_1_B_1_p_4 - C1*k_1_B_1_p_1 + C5*k_2_B_1_p_2 + C7*k_2_B_1_p_3 + C9*k_2_B_1_p_4], [C4*k_1_B_2_p_1 + C6*k_1_B_2_p_2 + C8*k_1_B_2_p_3 + C10*k_1_B_2_p_4 - C2*k_2_B_2_p_1 - C2*k_2_B_2_p_2 - C2*k_2_B_2_p_3 - C2*k_2_B_2_p_4], [C4*k_2_A_p_1 + C1*k_1_B_1_p_1 - C3*k_2_B_1_p_1 - C3*k_1_C_1_p_1_2 - C3*k_1_C_1_p_1_3 - C3*k_1_C_1_p_1_4 + C5*k_2_C_1_p_1_2 + C7*k_2_C_1_p_1_3 + C9*k_2_C_1_p_1_4 - C3*Leq*k_1_A_p_1], [C2*k_2_B_2_p_1 - C4*k_1_B_2_p_1 - C4*k_2_A_p_1 - C4*k_1_C_2_p_1_2 - C4*k_1_C_2_p_1_3 - C4*k_1_C_2_p_1_4 + C6*k_2_C_2_p_1_2 + C8*k_2_C_2_p_1_3 + C10*k_2_C_2_p_1_4 + C3*Leq*k_1_A_p_1], [C6*k_2_A_p_2 + C1*k_1_B_1_p_2 - C5*k_2_B_1_p_2 + C3*k_1_C_1_p_1_2 - C5*k_1_C_1_p_2_3 - C5*k_1_C_1_p_2_4 - C5*k_2_C_1_p_1_2 + C7*k_2_C_1_p_2_3 + C9*k_2_C_1_p_2_4 - C5*Leq*k_1_A_p_2], [C2*k_2_B_2_p_2 - C6*k_1_B_2_p_2 - C6*k_2_A_p_2 + C4*k_1_C_2_p_1_2 - C6*k_1_C_2_p_2_3 - C6*k_1_C_2_p_2_4 - C6*k_2_C_2_p_1_2 + C8*k_2_C_2_p_2_3 + C10*k_2_C_2_p_2_4 + C5*Leq*k_1_A_p_2], [C8*k_2_A_p_3 + C1*k_1_B_1_p_3 - C7*k_2_B_1_p_3 + C3*k_1_C_1_p_1_3 + C5*k_1_C_1_p_2_3 - C7*k_1_C_1_p_3_4 - C7*k_2_C_1_p_1_3 - C7*k_2_C_1_p_2_3 + C9*k_2_C_1_p_3_4 - C7*Leq*k_1_A_p_3], [C2*k_2_B_2_p_3 - C8*k_1_B_2_p_3 - C8*k_2_A_p_3 + C4*k_1_C_2_p_1_3 + C6*k_1_C_2_p_2_3 - C8*k_1_C_2_p_3_4 - C8*k_2_C_2_p_1_3 - C8*k_2_C_2_p_2_3 + C10*k_2_C_2_p_3_4 + C7*Leq*k_1_A_p_3], [C10*k_2_A_p_4 + C1*k_1_B_1_p_4 - C9*k_2_B_1_p_4 + C3*k_1_C_1_p_1_4 + C5*k_1_C_1_p_2_4 + C7*k_1_C_1_p_3_4 - C9*k_2_C_1_p_1_4 - C9*k_2_C_1_p_2_4 - C9*k_2_C_1_p_3_4 - C9*Leq*k_1_A_p_4], [C2*k_2_B_2_p_4 - C10*k_1_B_2_p_4 - C10*k_2_A_p_4 + C4*k_1_C_2_p_1_4 + C6*k_1_C_2_p_2_4 + C8*k_1_C_2_p_3_4 - C10*k_2_C_2_p_1_4 - C10*k_2_C_2_p_2_4 - C10*k_2_C_2_p_3_4 + C9*Leq*k_1_A_p_4]]) = matrix([[C3*k_2_B_1_p_1 - C1*k_1_B_1_p_2 - C1*k_1_B_1_p_3 - C1*k_1_B_1_p_4 - C1*k_1_B_1_p_1 + C5*k_2_B_1_p_2 + C7*k_2_B_1_p_3 + C9*k_2_B_1_p_4], [C4*k_1_B_2_p_1 + C6*k_1_B_2_p_2 + C8*k_1_B_2_p_3 + C10*k_1_B_2_p_4 - C2*k_2_B_2_p_1 - C2*k_2_B_2_p_2 - C2*k_2_B_2_p_3 - C2*k_2_B_2_p_4], [C4*k_2_A_p_1 + C1*k_1_B_1_p_1 - C3*k_2_B_1_p_1 - C3*k_1_C_1_p_1_2 - C3*k_1_C_1_p_1_3 - C3*k_1_C_1_p_1_4 + C5*k_2_C_1_p_1_2 + C7*k_2_C_1_p_1_3 + C9*k_2_C_1_p_1_4 - C3*Leq*k_1_A_p_1], [C2*k_2_B_2_p_1 - C4*k_1_B_2_p_1 - C4*k_2_A_p_1 - C4*k_1_C_2_p_1_2 - C4*k_1_C_2_p_1_3 - C4*k_1_C_2_p_1_4 + C6*k_2_C_2_p_1_2 + C8*k_2_C_2_p_1_3 + C10*k_2_C_2_p_1_4 + C3*Leq*k_1_A_p_1], [C6*k_2_A_p_2 + C1*k_1_B_1_p_2 - C5*k_2_B_1_p_2 + C3*k_1_C_1_p_1_2 - C5*k_1_C_1_p_2_3 - C5*k_1_C_1_p_2_4 - C5*k_2_C_1_p_1_2 + C7*k_2_C_1_p_2_3 + C9*k_2_C_1_p_2_4 - C5*Leq*k_1_A_p_2], [C2*k_2_B_2_p_2 - C6*k_1_B_2_p_2 - C6*k_2_A_p_2 + C4*k_1_C_2_p_1_2 - C6*k_1_C_2_p_2_3 - C6*k_1_C_2_p_2_4 - C6*k_2_C_2_p_1_2 + C8*k_2_C_2_p_2_3 + C10*k_2_C_2_p_2_4 + C5*Leq*k_1_A_p_2], [C8*k_2_A_p_3 + C1*k_1_B_1_p_3 - C7*k_2_B_1_p_3 + C3*k_1_C_1_p_1_3 + C5*k_1_C_1_p_2_3 - C7*k_1_C_1_p_3_4 - C7*k_2_C_1_p_1_3 - C7*k_2_C_1_p_2_3 + C9*k_2_C_1_p_3_4 - C7*Leq*k_1_A_p_3], [C2*k_2_B_2_p_3 - C8*k_1_B_2_p_3 - C8*k_2_A_p_3 + C4*k_1_C_2_p_1_3 + C6*k_1_C_2_p_2_3 - C8*k_1_C_2_p_3_4 - C8*k_2_C_2_p_1_3 - C8*k_2_C_2_p_2_3 + C10*k_2_C_2_p_3_4 + C7*Leq*k_1_A_p_3], [C10*k_2_A_p_4 + C1*k_1_B_1_p_4 - C9*k_2_B_1_p_4 + C3*k_1_C_1_p_1_4 + C5*k_1_C_1_p_2_4 + C7*k_1_C_1_p_3_4 - C9*k_2_C_1_p_1_4 - C9*k_2_C_1_p_2_4 - C9*k_2_C_1_p_3_4 - C9*Leq*k_1_A_p_4], [C2*k_2_B_2_p_4 - C10*k_1_B_2_p_4 - C10*k_2_A_p_4 + C4*k_1_C_2_p_1_4 + C6*k_1_C_2_p_2_4 + C8*k_1_C_2_p_3_4 - C10*k_2_C_2_p_1_4 - C10*k_2_C_2_p_2_4 - C10*k_2_C_2_p_3_4 + C9*Leq*k_1_A_p_4]])](5U_R_RL_images/math874.png)
![]()
Conclusion:
Typed K-matrix is correct
K matrix for the 4U-R-RL model
K;
![matrix([[- k_1_B_1_p_1 - k_1_B_1_p_2 - k_1_B_1_p_3 - k_1_B_1_p_4, 0, k_2_B_1_p_1, 0, k_2_B_1_p_2, 0, k_2_B_1_p_3, 0, k_2_B_1_p_4, 0], [0, - k_2_B_2_p_1 - k_2_B_2_p_2 - k_2_B_2_p_3 - k_2_B_2_p_4, 0, k_1_B_2_p_1, 0, k_1_B_2_p_2, 0, k_1_B_2_p_3, 0, k_1_B_2_p_4], [k_1_B_1_p_1, 0, - k_2_B_1_p_1 - k_1_C_1_p_1_2 - k_1_C_1_p_1_3 - k_1_C_1_p_1_4 - Leq*k_1_A_p_1, k_2_A_p_1, k_2_C_1_p_1_2, 0, k_2_C_1_p_1_3, 0, k_2_C_1_p_1_4, 0], [0, k_2_B_2_p_1, Leq*k_1_A_p_1, - k_2_A_p_1 - k_1_B_2_p_1 - k_1_C_2_p_1_2 - k_1_C_2_p_1_3 - k_1_C_2_p_1_4, 0, k_2_C_2_p_1_2, 0, k_2_C_2_p_1_3, 0, k_2_C_2_p_1_4], [k_1_B_1_p_2, 0, k_1_C_1_p_1_2, 0, - k_2_B_1_p_2 - k_1_C_1_p_2_3 - k_1_C_1_p_2_4 - k_2_C_1_p_1_2 - Leq*k_1_A_p_2, k_2_A_p_2, k_2_C_1_p_2_3, 0, k_2_C_1_p_2_4, 0], [0, k_2_B_2_p_2, 0, k_1_C_2_p_1_2, Leq*k_1_A_p_2, - k_2_A_p_2 - k_1_B_2_p_2 - k_1_C_2_p_2_3 - k_1_C_2_p_2_4 - k_2_C_2_p_1_2, 0, k_2_C_2_p_2_3, 0, k_2_C_2_p_2_4], [k_1_B_1_p_3, 0, k_1_C_1_p_1_3, 0, k_1_C_1_p_2_3, 0, - k_2_B_1_p_3 - k_1_C_1_p_3_4 - k_2_C_1_p_1_3 - k_2_C_1_p_2_3 - Leq*k_1_A_p_3, k_2_A_p_3, k_2_C_1_p_3_4, 0], [0, k_2_B_2_p_3, 0, k_1_C_2_p_1_3, 0, k_1_C_2_p_2_3, Leq*k_1_A_p_3, - k_2_A_p_3 - k_1_B_2_p_3 - k_1_C_2_p_3_4 - k_2_C_2_p_1_3 - k_2_C_2_p_2_3, 0, k_2_C_2_p_3_4], [k_1_B_1_p_4, 0, k_1_C_1_p_1_4, 0, k_1_C_1_p_2_4, 0, k_1_C_1_p_3_4, 0, - k_2_B_1_p_4 - k_2_C_1_p_1_4 - k_2_C_1_p_2_4 - k_2_C_1_p_3_4 - Leq*k_1_A_p_4, k_2_A_p_4], [0, k_2_B_2_p_4, 0, k_1_C_2_p_1_4, 0, k_1_C_2_p_2_4, 0, k_1_C_2_p_3_4, Leq*k_1_A_p_4, - k_2_A_p_4 - k_1_B_2_p_4 - k_2_C_2_p_1_4 - k_2_C_2_p_2_4 - k_2_C_2_p_3_4]])](5U_R_RL_images/math876.png)
Expession of K matrix for U-5R-RL mechanism
Order of species to allow for easy expansion of matrices:
R*, RL*, R', RL', R'', RL'', R''', RL''', R'''', RL'''', R''''', RL'''''
Summary list of the net rate equations for the mechanism
eq_Rs_N__5U_R_RL;
eq_RLs_N__5U_R_RL;
eq_Rp1_N__5U_R_RL;
eq_RLp1_N__5U_R_RL;
eq_Rp2_N__5U_R_RL;
eq_Rp2_N__5U_R_RL;
eq_RLp2_N__5U_R_RL;
eq_Rp3_N__5U_R_RL;
eq_RLp3_N__5U_R_RL;
eq_Rp4_N__5U_R_RL;
eq_RLp4_N__5U_R_RL;
eq_Rp5_N__5U_R_RL;
eq_RLp5_N__5U_R_RL;
![]()



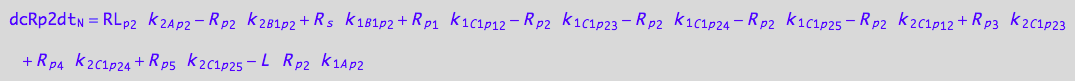
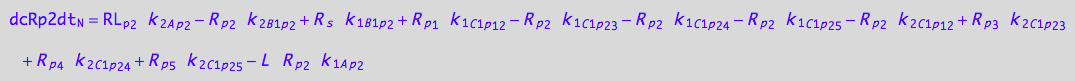

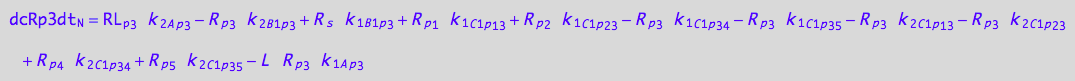
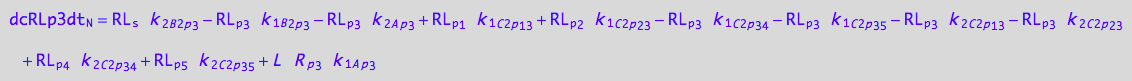
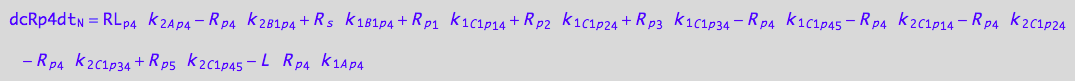
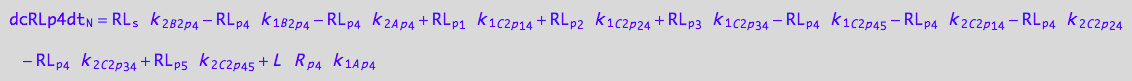

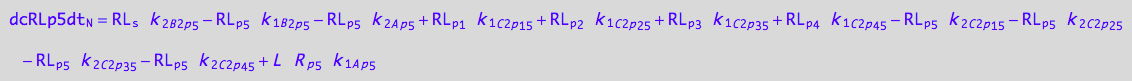
Assign sequential names to species
feq_1a:= R_s = C1;
feq_1b:= RL_s = C2;
feq_1c:= R_p_1 = C3;
feq_1d:= RL_p_1 = C4;
feq_1e:= R_p_2 = C5;
feq_1f:= RL_p_2 = C6;
feq_1g:= R_p_3 = C7;
feq_1h:= RL_p_3 = C8;
feq_1i:= R_p_4 = C9;
feq_1j:= RL_p_4 = C10;
feq_1k:= R_p_5 = C11;
feq_1l:= RL_p_5 = C12;
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Assign the same order to net rate equations
feq_2a:= dcRsdt_N = dC1dt;
feq_2b:= dcRLsdt_N = dC2dt;
feq_2c:= dcRp1dt_N = dC3dt;
feq_2d:= dcRLp1dt_N = dC4dt;
feq_2e:= dcRp2dt_N = dC5dt;
feq_2f:= dcRLp2dt_N = dC6dt;
feq_2g:= dcRp3dt_N = dC7dt;
feq_2h:= dcRLp3dt_N = dC8dt;
feq_2i:= dcRp4dt_N = dC9dt;
feq_2j:= dcRLp4dt_N = dC10dt;
feq_2k:= dcRp5dt_N = dC11dt;
feq_2l:= dcRLp5dt_N = dC12dt;
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Restate the equations in terms of new sequential species names (rename free ligand concentration too)
R*
eq_Rs_N__5U_R_RL;
feq_3a:= % |\
feq_1a | feq_2a | \
feq_1b | feq_2b | \
feq_1c | feq_2c | \
feq_1d | feq_2d | \
feq_1e | feq_2e | \
feq_1f | feq_2f | \
feq_1g | feq_2g | \
feq_1h | feq_2h | \
feq_1i | feq_2i | \
feq_1j | feq_2j | \
feq_1k | feq_2k | \
feq_1l | feq_2l | \
L = Leq
![]()
![]()
RL*
eq_RLs_N__5U_R_RL;
feq_3b:= % |\
feq_1a | feq_2a | \
feq_1b | feq_2b | \
feq_1c | feq_2c | \
feq_1d | feq_2d | \
feq_1e | feq_2e | \
feq_1f | feq_2f | \
feq_1g | feq_2g | \
feq_1h | feq_2h | \
feq_1i | feq_2i | \
feq_1j | feq_2j | \
feq_1k | feq_2k | \
feq_1l | feq_2l | \
L = Leq

![]()
R'
eq_Rp1_N__5U_R_RL;
feq_3c:= % |\
feq_1a | feq_2a | \
feq_1b | feq_2b | \
feq_1c | feq_2c | \
feq_1d | feq_2d | \
feq_1e | feq_2e | \
feq_1f | feq_2f | \
feq_1g | feq_2g | \
feq_1h | feq_2h | \
feq_1i | feq_2i | \
feq_1j | feq_2j | \
feq_1k | feq_2k | \
feq_1l | feq_2l | \
L = Leq


RL'
eq_RLp1_N__5U_R_RL;
feq_3d:= % |\
feq_1a | feq_2a | \
feq_1b | feq_2b | \
feq_1c | feq_2c | \
feq_1d | feq_2d | \
feq_1e | feq_2e | \
feq_1f | feq_2f | \
feq_1g | feq_2g | \
feq_1h | feq_2h | \
feq_1i | feq_2i | \
feq_1j | feq_2j | \
feq_1k | feq_2k | \
feq_1l | feq_2l | \
L = Leq


R''
eq_Rp2_N__5U_R_RL;
feq_3e:= % |\
feq_1a | feq_2a | \
feq_1b | feq_2b | \
feq_1c | feq_2c | \
feq_1d | feq_2d | \
feq_1e | feq_2e | \
feq_1f | feq_2f | \
feq_1g | feq_2g | \
feq_1h | feq_2h | \
feq_1i | feq_2i | \
feq_1j | feq_2j | \
feq_1k | feq_2k | \
feq_1l | feq_2l | \
L = Leq
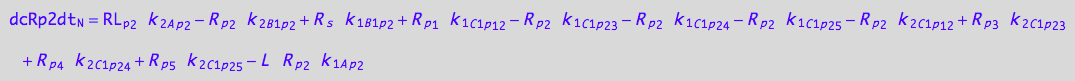

RL''
eq_RLp2_N__5U_R_RL;
feq_3f:= % |\
feq_1a | feq_2a | \
feq_1b | feq_2b | \
feq_1c | feq_2c | \
feq_1d | feq_2d | \
feq_1e | feq_2e | \
feq_1f | feq_2f | \
feq_1g | feq_2g | \
feq_1h | feq_2h | \
feq_1i | feq_2i | \
feq_1j | feq_2j | \
feq_1k | feq_2k | \
feq_1l | feq_2l | \
L = Leq


R'''
eq_Rp3_N__5U_R_RL;
feq_3g:= % |\
feq_1a | feq_2a | \
feq_1b | feq_2b | \
feq_1c | feq_2c | \
feq_1d | feq_2d | \
feq_1e | feq_2e | \
feq_1f | feq_2f | \
feq_1g | feq_2g | \
feq_1h | feq_2h | \
feq_1i | feq_2i | \
feq_1j | feq_2j | \
feq_1k | feq_2k | \
feq_1l | feq_2l | \
L = Leq
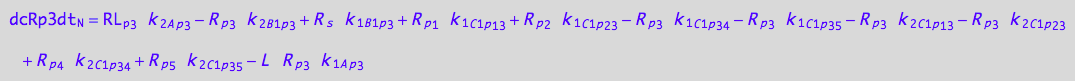

RL'''
eq_RLp3_N__5U_R_RL;
feq_3h:= % |\
feq_1a | feq_2a | \
feq_1b | feq_2b | \
feq_1c | feq_2c | \
feq_1d | feq_2d | \
feq_1e | feq_2e | \
feq_1f | feq_2f | \
feq_1g | feq_2g | \
feq_1h | feq_2h | \
feq_1i | feq_2i | \
feq_1j | feq_2j | \
feq_1k | feq_2k | \
feq_1l | feq_2l | \
L = Leq
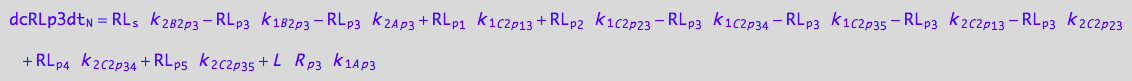

R''''
eq_Rp4_N__5U_R_RL;
feq_3i:= % |\
feq_1a | feq_2a | \
feq_1b | feq_2b | \
feq_1c | feq_2c | \
feq_1d | feq_2d | \
feq_1e | feq_2e | \
feq_1f | feq_2f | \
feq_1g | feq_2g | \
feq_1h | feq_2h | \
feq_1i | feq_2i | \
feq_1j | feq_2j | \
feq_1k | feq_2k | \
feq_1l | feq_2l | \
L = Leq
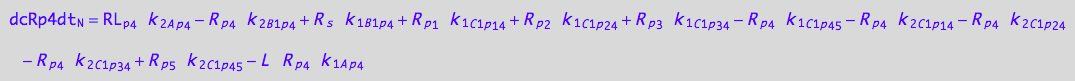
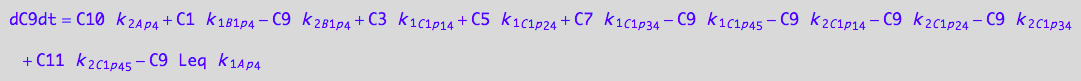
RL''''
eq_RLp4_N__5U_R_RL;
feq_3j:= % |\
feq_1a | feq_2a | \
feq_1b | feq_2b | \
feq_1c | feq_2c | \
feq_1d | feq_2d | \
feq_1e | feq_2e | \
feq_1f | feq_2f | \
feq_1g | feq_2g | \
feq_1h | feq_2h | \
feq_1i | feq_2i | \
feq_1j | feq_2j | \
feq_1k | feq_2k | \
feq_1l | feq_2l | \
L = Leq
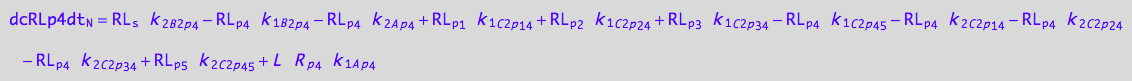

R'''''
eq_Rp5_N__5U_R_RL;
feq_3k:= % |\
feq_1a | feq_2a | \
feq_1b | feq_2b | \
feq_1c | feq_2c | \
feq_1d | feq_2d | \
feq_1e | feq_2e | \
feq_1f | feq_2f | \
feq_1g | feq_2g | \
feq_1h | feq_2h | \
feq_1i | feq_2i | \
feq_1j | feq_2j | \
feq_1k | feq_2k | \
feq_1l | feq_2l | \
L = Leq


RL'''''
eq_RLp5_N__5U_R_RL;
feq_3l:= % |\
feq_1a | feq_2a | \
feq_1b | feq_2b | \
feq_1c | feq_2c | \
feq_1d | feq_2d | \
feq_1e | feq_2e | \
feq_1f | feq_2f | \
feq_1g | feq_2g | \
feq_1h | feq_2h | \
feq_1i | feq_2i | \
feq_1j | feq_2j | \
feq_1k | feq_2k | \
feq_1l | feq_2l | \
L = Leq
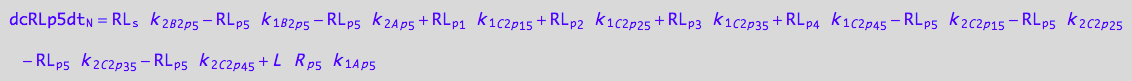

Prepare results for transfer to MATLAB
See Workflow for accurate extraction of the K matrix
Simple rules that allow catching mistakes in K matrix derivation:
(1) a sum of each column should be zero (so each constant must appear with both positive and negative sign), and
(2) each row has to have complete pairs of constants (i.e., if k12
appears there must be k21 in the same row with an opposite sign and so on).
K:=matrix(12,12,[
[ -k_1_B_1_p_2 -k_1_B_1_p_3 -k_1_B_1_p_4 -k_1_B_1_p_5 -k_1_B_1_p_1, 0, k_2_B_1_p_1, 0, +k_2_B_1_p_2, 0, +k_2_B_1_p_3, 0, +k_2_B_1_p_4, 0, +k_2_B_1_p_5, 0 ],
[ 0, -k_2_B_2_p_1 -k_2_B_2_p_2 -k_2_B_2_p_3 -k_2_B_2_p_4 -k_2_B_2_p_5, 0, k_1_B_2_p_1, 0, +k_1_B_2_p_2, 0, +k_1_B_2_p_3, 0, +k_1_B_2_p_4, 0, +k_1_B_2_p_5 ],
[ +k_1_B_1_p_1, 0, -k_2_B_1_p_1 -k_1_C_1_p_1_2 -k_1_C_1_p_1_3 -k_1_C_1_p_1_4 -k_1_C_1_p_1_5 -Leq*k_1_A_p_1, k_2_A_p_1, +k_2_C_1_p_1_2, 0, +k_2_C_1_p_1_3, 0, +k_2_C_1_p_1_4, 0, +k_2_C_1_p_1_5, 0 ],
[ 0, k_2_B_2_p_1, +Leq*k_1_A_p_1, -k_1_B_2_p_1 -k_2_A_p_1 -k_1_C_2_p_1_2 -k_1_C_2_p_1_3 -k_1_C_2_p_1_4 -k_1_C_2_p_1_5, 0, +k_2_C_2_p_1_2, 0, +k_2_C_2_p_1_3, 0, +k_2_C_2_p_1_4, 0, +k_2_C_2_p_1_5 ],
[ +k_1_B_1_p_2, 0, +k_1_C_1_p_1_2, 0, -k_2_B_1_p_2 -k_1_C_1_p_2_3 -k_1_C_1_p_2_4 -k_1_C_1_p_2_5 -k_2_C_1_p_1_2 -Leq*k_1_A_p_2, k_2_A_p_2, +k_2_C_1_p_2_3, 0, +k_2_C_1_p_2_4, 0, +k_2_C_1_p_2_5, 0 ],
[ 0, k_2_B_2_p_2, 0, +k_1_C_2_p_1_2, +Leq*k_1_A_p_2, -k_1_B_2_p_2 -k_2_A_p_2 -k_1_C_2_p_2_3 -k_1_C_2_p_2_4 -k_1_C_2_p_2_5 -k_2_C_2_p_1_2, 0, +k_2_C_2_p_2_3, 0, +k_2_C_2_p_2_4, 0, +k_2_C_2_p_2_5 ],
[ +k_1_B_1_p_3, 0, +k_1_C_1_p_1_3, 0,+k_1_C_1_p_2_3, 0, -k_2_B_1_p_3 -k_1_C_1_p_3_4 -k_1_C_1_p_3_5 -k_2_C_1_p_1_3 -k_2_C_1_p_2_3 -Leq*k_1_A_p_3, k_2_A_p_3, +k_2_C_1_p_3_4, 0, +k_2_C_1_p_3_5, 0 ],
[ 0, k_2_B_2_p_3, 0, +k_1_C_2_p_1_3, 0, +k_1_C_2_p_2_3, +Leq*k_1_A_p_3, -k_1_B_2_p_3 -k_2_A_p_3 -k_1_C_2_p_3_4 -k_1_C_2_p_3_5 -k_2_C_2_p_1_3 -k_2_C_2_p_2_3, 0, +k_2_C_2_p_3_4, 0, +k_2_C_2_p_3_5 ],
[ +k_1_B_1_p_4, 0, +k_1_C_1_p_1_4, 0, +k_1_C_1_p_2_4, 0, +k_1_C_1_p_3_4, 0, -k_2_B_1_p_4 -k_1_C_1_p_4_5 -k_2_C_1_p_1_4 -k_2_C_1_p_2_4 -k_2_C_1_p_3_4 -Leq*k_1_A_p_4, k_2_A_p_4, +k_2_C_1_p_4_5, 0 ],
[ 0, k_2_B_2_p_4, 0, +k_1_C_2_p_1_4, 0, +k_1_C_2_p_2_4, 0, +k_1_C_2_p_3_4, +Leq*k_1_A_p_4, -k_1_B_2_p_4 -k_2_A_p_4 -k_1_C_2_p_4_5 -k_2_C_2_p_1_4 -k_2_C_2_p_2_4 -k_2_C_2_p_3_4, 0, +k_2_C_2_p_4_5 ],
[ +k_1_B_1_p_5, 0, +k_1_C_1_p_1_5, 0, +k_1_C_1_p_2_5, 0, +k_1_C_1_p_3_5, 0, +k_1_C_1_p_4_5, 0, -k_2_B_1_p_5 -k_2_C_1_p_1_5 -k_2_C_1_p_2_5 -k_2_C_1_p_3_5 -k_2_C_1_p_4_5 -Leq*k_1_A_p_5, k_2_A_p_5 ],
[ 0, k_2_B_2_p_5, 0, +k_1_C_2_p_1_5, 0, +k_1_C_2_p_2_5, 0, +k_1_C_2_p_3_5, 0, +k_1_C_2_p_4_5, +Leq*k_1_A_p_5, -k_1_B_2_p_5 -k_2_A_p_5 -k_2_C_2_p_1_5 -k_2_C_2_p_2_5 -k_2_C_2_p_3_5 -k_2_C_2_p_4_5 ]
])
![matrix([[- k_1_B_1_p_1 - k_1_B_1_p_2 - k_1_B_1_p_3 - k_1_B_1_p_4 - k_1_B_1_p_5, 0, k_2_B_1_p_1, 0, k_2_B_1_p_2, 0, k_2_B_1_p_3, 0, k_2_B_1_p_4, 0, k_2_B_1_p_5, 0], [0, - k_2_B_2_p_1 - k_2_B_2_p_2 - k_2_B_2_p_3 - k_2_B_2_p_4 - k_2_B_2_p_5, 0, k_1_B_2_p_1, 0, k_1_B_2_p_2, 0, k_1_B_2_p_3, 0, k_1_B_2_p_4, 0, k_1_B_2_p_5], [k_1_B_1_p_1, 0, - k_2_B_1_p_1 - k_1_C_1_p_1_2 - k_1_C_1_p_1_3 - k_1_C_1_p_1_4 - k_1_C_1_p_1_5 - Leq*k_1_A_p_1, k_2_A_p_1, k_2_C_1_p_1_2, 0, k_2_C_1_p_1_3, 0, k_2_C_1_p_1_4, 0, k_2_C_1_p_1_5, 0], [0, k_2_B_2_p_1, Leq*k_1_A_p_1, - k_2_A_p_1 - k_1_B_2_p_1 - k_1_C_2_p_1_2 - k_1_C_2_p_1_3 - k_1_C_2_p_1_4 - k_1_C_2_p_1_5, 0, k_2_C_2_p_1_2, 0, k_2_C_2_p_1_3, 0, k_2_C_2_p_1_4, 0, k_2_C_2_p_1_5], [k_1_B_1_p_2, 0, k_1_C_1_p_1_2, 0, - k_2_B_1_p_2 - k_1_C_1_p_2_3 - k_1_C_1_p_2_4 - k_1_C_1_p_2_5 - k_2_C_1_p_1_2 - Leq*k_1_A_p_2, k_2_A_p_2, k_2_C_1_p_2_3, 0, k_2_C_1_p_2_4, 0, k_2_C_1_p_2_5, 0], [0, k_2_B_2_p_2, 0, k_1_C_2_p_1_2, Leq*k_1_A_p_2, - k_2_A_p_2 - k_1_B_2_p_2 - k_1_C_2_p_2_3 - k_1_C_2_p_2_4 - k_1_C_2_p_2_5 - k_2_C_2_p_1_2, 0, k_2_C_2_p_2_3, 0, k_2_C_2_p_2_4, 0, k_2_C_2_p_2_5], [k_1_B_1_p_3, 0, k_1_C_1_p_1_3, 0, k_1_C_1_p_2_3, 0, - k_2_B_1_p_3 - k_1_C_1_p_3_4 - k_1_C_1_p_3_5 - k_2_C_1_p_1_3 - k_2_C_1_p_2_3 - Leq*k_1_A_p_3, k_2_A_p_3, k_2_C_1_p_3_4, 0, k_2_C_1_p_3_5, 0], [0, k_2_B_2_p_3, 0, k_1_C_2_p_1_3, 0, k_1_C_2_p_2_3, Leq*k_1_A_p_3, - k_2_A_p_3 - k_1_B_2_p_3 - k_1_C_2_p_3_4 - k_1_C_2_p_3_5 - k_2_C_2_p_1_3 - k_2_C_2_p_2_3, 0, k_2_C_2_p_3_4, 0, k_2_C_2_p_3_5], [k_1_B_1_p_4, 0, k_1_C_1_p_1_4, 0, k_1_C_1_p_2_4, 0, k_1_C_1_p_3_4, 0, - k_2_B_1_p_4 - k_1_C_1_p_4_5 - k_2_C_1_p_1_4 - k_2_C_1_p_2_4 - k_2_C_1_p_3_4 - Leq*k_1_A_p_4, k_2_A_p_4, k_2_C_1_p_4_5, 0], [0, k_2_B_2_p_4, 0, k_1_C_2_p_1_4, 0, k_1_C_2_p_2_4, 0, k_1_C_2_p_3_4, Leq*k_1_A_p_4, - k_2_A_p_4 - k_1_B_2_p_4 - k_1_C_2_p_4_5 - k_2_C_2_p_1_4 - k_2_C_2_p_2_4 - k_2_C_2_p_3_4, 0, k_2_C_2_p_4_5], [k_1_B_1_p_5, 0, k_1_C_1_p_1_5, 0, k_1_C_1_p_2_5, 0, k_1_C_1_p_3_5, 0, k_1_C_1_p_4_5, 0, - k_2_B_1_p_5 - k_2_C_1_p_1_5 - k_2_C_1_p_2_5 - k_2_C_1_p_3_5 - k_2_C_1_p_4_5 - Leq*k_1_A_p_5, k_2_A_p_5], [0, k_2_B_2_p_5, 0, k_1_C_2_p_1_5, 0, k_1_C_2_p_2_5, 0, k_1_C_2_p_3_5, 0, k_1_C_2_p_4_5, Leq*k_1_A_p_5, - k_2_A_p_5 - k_1_B_2_p_5 - k_2_C_2_p_1_5 - k_2_C_2_p_2_5 - k_2_C_2_p_3_5 - k_2_C_2_p_4_5]])](5U_R_RL_images/math938.png)
Test the K matrix entry
Create a column vector of species concentrations
P:=matrix(12,1,[C1, C2, C3, C4, C5, C6, C7, C8, C9, C10, C11, C12])
![matrix([[C1], [C2], [C3], [C4], [C5], [C6], [C7], [C8], [C9], [C10], [C11], [C12]])](5U_R_RL_images/math939.png)
Multiply K and P:
dCdt_manual_input:= K*P
![matrix([[C3*k_2_B_1_p_1 + C5*k_2_B_1_p_2 + C7*k_2_B_1_p_3 + C9*k_2_B_1_p_4 + C11*k_2_B_1_p_5 - C1*(k_1_B_1_p_1 + k_1_B_1_p_2 + k_1_B_1_p_3 + k_1_B_1_p_4 + k_1_B_1_p_5)], [C4*k_1_B_2_p_1 + C6*k_1_B_2_p_2 + C8*k_1_B_2_p_3 + C10*k_1_B_2_p_4 + C12*k_1_B_2_p_5 - C2*(k_2_B_2_p_1 + k_2_B_2_p_2 + k_2_B_2_p_3 + k_2_B_2_p_4 + k_2_B_2_p_5)], [C4*k_2_A_p_1 + C1*k_1_B_1_p_1 + C5*k_2_C_1_p_1_2 + C7*k_2_C_1_p_1_3 + C9*k_2_C_1_p_1_4 + C11*k_2_C_1_p_1_5 - C3*(k_2_B_1_p_1 + k_1_C_1_p_1_2 + k_1_C_1_p_1_3 + k_1_C_1_p_1_4 + k_1_C_1_p_1_5 + Leq*k_1_A_p_1)], [C2*k_2_B_2_p_1 + C6*k_2_C_2_p_1_2 + C8*k_2_C_2_p_1_3 + C10*k_2_C_2_p_1_4 + C12*k_2_C_2_p_1_5 - C4*(k_2_A_p_1 + k_1_B_2_p_1 + k_1_C_2_p_1_2 + k_1_C_2_p_1_3 + k_1_C_2_p_1_4 + k_1_C_2_p_1_5) + C3*Leq*k_1_A_p_1], [C6*k_2_A_p_2 + C1*k_1_B_1_p_2 + C3*k_1_C_1_p_1_2 + C7*k_2_C_1_p_2_3 + C9*k_2_C_1_p_2_4 + C11*k_2_C_1_p_2_5 - C5*(k_2_B_1_p_2 + k_1_C_1_p_2_3 + k_1_C_1_p_2_4 + k_1_C_1_p_2_5 + k_2_C_1_p_1_2 + Leq*k_1_A_p_2)], [C2*k_2_B_2_p_2 + C4*k_1_C_2_p_1_2 + C8*k_2_C_2_p_2_3 + C10*k_2_C_2_p_2_4 + C12*k_2_C_2_p_2_5 - C6*(k_2_A_p_2 + k_1_B_2_p_2 + k_1_C_2_p_2_3 + k_1_C_2_p_2_4 + k_1_C_2_p_2_5 + k_2_C_2_p_1_2) + C5*Leq*k_1_A_p_2], [C8*k_2_A_p_3 + C1*k_1_B_1_p_3 + C3*k_1_C_1_p_1_3 + C5*k_1_C_1_p_2_3 + C9*k_2_C_1_p_3_4 + C11*k_2_C_1_p_3_5 - C7*(k_2_B_1_p_3 + k_1_C_1_p_3_4 + k_1_C_1_p_3_5 + k_2_C_1_p_1_3 + k_2_C_1_p_2_3 + Leq*k_1_A_p_3)], [C2*k_2_B_2_p_3 + C4*k_1_C_2_p_1_3 + C6*k_1_C_2_p_2_3 + C10*k_2_C_2_p_3_4 + C12*k_2_C_2_p_3_5 - C8*(k_2_A_p_3 + k_1_B_2_p_3 + k_1_C_2_p_3_4 + k_1_C_2_p_3_5 + k_2_C_2_p_1_3 + k_2_C_2_p_2_3) + C7*Leq*k_1_A_p_3], [C10*k_2_A_p_4 + C1*k_1_B_1_p_4 + C3*k_1_C_1_p_1_4 + C5*k_1_C_1_p_2_4 + C7*k_1_C_1_p_3_4 + C11*k_2_C_1_p_4_5 - C9*(k_2_B_1_p_4 + k_1_C_1_p_4_5 + k_2_C_1_p_1_4 + k_2_C_1_p_2_4 + k_2_C_1_p_3_4 + Leq*k_1_A_p_4)], [C2*k_2_B_2_p_4 + C4*k_1_C_2_p_1_4 + C6*k_1_C_2_p_2_4 + C8*k_1_C_2_p_3_4 + C12*k_2_C_2_p_4_5 - C10*(k_2_A_p_4 + k_1_B_2_p_4 + k_1_C_2_p_4_5 + k_2_C_2_p_1_4 + k_2_C_2_p_2_4 + k_2_C_2_p_3_4) + C9*Leq*k_1_A_p_4], [C12*k_2_A_p_5 + C1*k_1_B_1_p_5 + C3*k_1_C_1_p_1_5 + C5*k_1_C_1_p_2_5 + C7*k_1_C_1_p_3_5 + C9*k_1_C_1_p_4_5 - C11*(k_2_B_1_p_5 + k_2_C_1_p_1_5 + k_2_C_1_p_2_5 + k_2_C_1_p_3_5 + k_2_C_1_p_4_5 + Leq*k_1_A_p_5)], [C2*k_2_B_2_p_5 + C4*k_1_C_2_p_1_5 + C6*k_1_C_2_p_2_5 + C8*k_1_C_2_p_3_5 + C10*k_1_C_2_p_4_5 - C12*(k_2_A_p_5 + k_1_B_2_p_5 + k_2_C_2_p_1_5 + k_2_C_2_p_2_5 + k_2_C_2_p_3_5 + k_2_C_2_p_4_5) + C11*Leq*k_1_A_p_5]])](5U_R_RL_images/math940.png)
Collect right-hand-side parts of net rate equations expressed in sequential species names
dCdt_mupad:=matrix(12,1,[ rhs(feq_3a), rhs(feq_3b), rhs(feq_3c), rhs(feq_3d), rhs(feq_3e), rhs(feq_3f), rhs(feq_3g), rhs(feq_3h), rhs(feq_3i), rhs(feq_3j), rhs(feq_3k), rhs(feq_3l)])
![matrix([[C3*k_2_B_1_p_1 - C1*k_1_B_1_p_2 - C1*k_1_B_1_p_3 - C1*k_1_B_1_p_4 - C1*k_1_B_1_p_5 - C1*k_1_B_1_p_1 + C5*k_2_B_1_p_2 + C7*k_2_B_1_p_3 + C9*k_2_B_1_p_4 + C11*k_2_B_1_p_5], [C4*k_1_B_2_p_1 + C6*k_1_B_2_p_2 + C8*k_1_B_2_p_3 + C10*k_1_B_2_p_4 + C12*k_1_B_2_p_5 - C2*k_2_B_2_p_1 - C2*k_2_B_2_p_2 - C2*k_2_B_2_p_3 - C2*k_2_B_2_p_4 - C2*k_2_B_2_p_5], [C4*k_2_A_p_1 + C1*k_1_B_1_p_1 - C3*k_2_B_1_p_1 - C3*k_1_C_1_p_1_2 - C3*k_1_C_1_p_1_3 - C3*k_1_C_1_p_1_4 - C3*k_1_C_1_p_1_5 + C5*k_2_C_1_p_1_2 + C7*k_2_C_1_p_1_3 + C9*k_2_C_1_p_1_4 + C11*k_2_C_1_p_1_5 - C3*Leq*k_1_A_p_1], [C2*k_2_B_2_p_1 - C4*k_1_B_2_p_1 - C4*k_2_A_p_1 - C4*k_1_C_2_p_1_2 - C4*k_1_C_2_p_1_3 - C4*k_1_C_2_p_1_4 - C4*k_1_C_2_p_1_5 + C6*k_2_C_2_p_1_2 + C8*k_2_C_2_p_1_3 + C10*k_2_C_2_p_1_4 + C12*k_2_C_2_p_1_5 + C3*Leq*k_1_A_p_1], [C6*k_2_A_p_2 + C1*k_1_B_1_p_2 - C5*k_2_B_1_p_2 + C3*k_1_C_1_p_1_2 - C5*k_1_C_1_p_2_3 - C5*k_1_C_1_p_2_4 - C5*k_1_C_1_p_2_5 - C5*k_2_C_1_p_1_2 + C7*k_2_C_1_p_2_3 + C9*k_2_C_1_p_2_4 + C11*k_2_C_1_p_2_5 - C5*Leq*k_1_A_p_2], [C2*k_2_B_2_p_2 - C6*k_1_B_2_p_2 - C6*k_2_A_p_2 + C4*k_1_C_2_p_1_2 - C6*k_1_C_2_p_2_3 - C6*k_1_C_2_p_2_4 - C6*k_1_C_2_p_2_5 - C6*k_2_C_2_p_1_2 + C8*k_2_C_2_p_2_3 + C10*k_2_C_2_p_2_4 + C12*k_2_C_2_p_2_5 + C5*Leq*k_1_A_p_2], [C8*k_2_A_p_3 + C1*k_1_B_1_p_3 - C7*k_2_B_1_p_3 + C3*k_1_C_1_p_1_3 + C5*k_1_C_1_p_2_3 - C7*k_1_C_1_p_3_4 - C7*k_1_C_1_p_3_5 - C7*k_2_C_1_p_1_3 - C7*k_2_C_1_p_2_3 + C9*k_2_C_1_p_3_4 + C11*k_2_C_1_p_3_5 - C7*Leq*k_1_A_p_3], [C2*k_2_B_2_p_3 - C8*k_1_B_2_p_3 - C8*k_2_A_p_3 + C4*k_1_C_2_p_1_3 + C6*k_1_C_2_p_2_3 - C8*k_1_C_2_p_3_4 - C8*k_1_C_2_p_3_5 - C8*k_2_C_2_p_1_3 - C8*k_2_C_2_p_2_3 + C10*k_2_C_2_p_3_4 + C12*k_2_C_2_p_3_5 + C7*Leq*k_1_A_p_3], [C10*k_2_A_p_4 + C1*k_1_B_1_p_4 - C9*k_2_B_1_p_4 + C3*k_1_C_1_p_1_4 + C5*k_1_C_1_p_2_4 + C7*k_1_C_1_p_3_4 - C9*k_1_C_1_p_4_5 - C9*k_2_C_1_p_1_4 - C9*k_2_C_1_p_2_4 - C9*k_2_C_1_p_3_4 + C11*k_2_C_1_p_4_5 - C9*Leq*k_1_A_p_4], [C2*k_2_B_2_p_4 - C10*k_1_B_2_p_4 - C10*k_2_A_p_4 + C4*k_1_C_2_p_1_4 + C6*k_1_C_2_p_2_4 + C8*k_1_C_2_p_3_4 - C10*k_1_C_2_p_4_5 - C10*k_2_C_2_p_1_4 - C10*k_2_C_2_p_2_4 - C10*k_2_C_2_p_3_4 + C12*k_2_C_2_p_4_5 + C9*Leq*k_1_A_p_4], [C12*k_2_A_p_5 + C1*k_1_B_1_p_5 - C11*k_2_B_1_p_5 + C3*k_1_C_1_p_1_5 + C5*k_1_C_1_p_2_5 + C7*k_1_C_1_p_3_5 + C9*k_1_C_1_p_4_5 - C11*k_2_C_1_p_1_5 - C11*k_2_C_1_p_2_5 - C11*k_2_C_1_p_3_5 - C11*k_2_C_1_p_4_5 - C11*Leq*k_1_A_p_5], [C2*k_2_B_2_p_5 - C12*k_1_B_2_p_5 - C12*k_2_A_p_5 + C4*k_1_C_2_p_1_5 + C6*k_1_C_2_p_2_5 + C8*k_1_C_2_p_3_5 + C10*k_1_C_2_p_4_5 - C12*k_2_C_2_p_1_5 - C12*k_2_C_2_p_2_5 - C12*k_2_C_2_p_3_5 - C12*k_2_C_2_p_4_5 + C11*Leq*k_1_A_p_5]])](5U_R_RL_images/math941.png)
Compare derivation result to manual input
dCdt_mupad=dCdt_manual_input:
normal(%);
bool(%)
![matrix([[C3*k_2_B_1_p_1 - C1*k_1_B_1_p_2 - C1*k_1_B_1_p_3 - C1*k_1_B_1_p_4 - C1*k_1_B_1_p_5 - C1*k_1_B_1_p_1 + C5*k_2_B_1_p_2 + C7*k_2_B_1_p_3 + C9*k_2_B_1_p_4 + C11*k_2_B_1_p_5], [C4*k_1_B_2_p_1 + C6*k_1_B_2_p_2 + C8*k_1_B_2_p_3 + C10*k_1_B_2_p_4 + C12*k_1_B_2_p_5 - C2*k_2_B_2_p_1 - C2*k_2_B_2_p_2 - C2*k_2_B_2_p_3 - C2*k_2_B_2_p_4 - C2*k_2_B_2_p_5], [C4*k_2_A_p_1 + C1*k_1_B_1_p_1 - C3*k_2_B_1_p_1 - C3*k_1_C_1_p_1_2 - C3*k_1_C_1_p_1_3 - C3*k_1_C_1_p_1_4 - C3*k_1_C_1_p_1_5 + C5*k_2_C_1_p_1_2 + C7*k_2_C_1_p_1_3 + C9*k_2_C_1_p_1_4 + C11*k_2_C_1_p_1_5 - C3*Leq*k_1_A_p_1], [C2*k_2_B_2_p_1 - C4*k_1_B_2_p_1 - C4*k_2_A_p_1 - C4*k_1_C_2_p_1_2 - C4*k_1_C_2_p_1_3 - C4*k_1_C_2_p_1_4 - C4*k_1_C_2_p_1_5 + C6*k_2_C_2_p_1_2 + C8*k_2_C_2_p_1_3 + C10*k_2_C_2_p_1_4 + C12*k_2_C_2_p_1_5 + C3*Leq*k_1_A_p_1], [C6*k_2_A_p_2 + C1*k_1_B_1_p_2 - C5*k_2_B_1_p_2 + C3*k_1_C_1_p_1_2 - C5*k_1_C_1_p_2_3 - C5*k_1_C_1_p_2_4 - C5*k_1_C_1_p_2_5 - C5*k_2_C_1_p_1_2 + C7*k_2_C_1_p_2_3 + C9*k_2_C_1_p_2_4 + C11*k_2_C_1_p_2_5 - C5*Leq*k_1_A_p_2], [C2*k_2_B_2_p_2 - C6*k_1_B_2_p_2 - C6*k_2_A_p_2 + C4*k_1_C_2_p_1_2 - C6*k_1_C_2_p_2_3 - C6*k_1_C_2_p_2_4 - C6*k_1_C_2_p_2_5 - C6*k_2_C_2_p_1_2 + C8*k_2_C_2_p_2_3 + C10*k_2_C_2_p_2_4 + C12*k_2_C_2_p_2_5 + C5*Leq*k_1_A_p_2], [C8*k_2_A_p_3 + C1*k_1_B_1_p_3 - C7*k_2_B_1_p_3 + C3*k_1_C_1_p_1_3 + C5*k_1_C_1_p_2_3 - C7*k_1_C_1_p_3_4 - C7*k_1_C_1_p_3_5 - C7*k_2_C_1_p_1_3 - C7*k_2_C_1_p_2_3 + C9*k_2_C_1_p_3_4 + C11*k_2_C_1_p_3_5 - C7*Leq*k_1_A_p_3], [C2*k_2_B_2_p_3 - C8*k_1_B_2_p_3 - C8*k_2_A_p_3 + C4*k_1_C_2_p_1_3 + C6*k_1_C_2_p_2_3 - C8*k_1_C_2_p_3_4 - C8*k_1_C_2_p_3_5 - C8*k_2_C_2_p_1_3 - C8*k_2_C_2_p_2_3 + C10*k_2_C_2_p_3_4 + C12*k_2_C_2_p_3_5 + C7*Leq*k_1_A_p_3], [C10*k_2_A_p_4 + C1*k_1_B_1_p_4 - C9*k_2_B_1_p_4 + C3*k_1_C_1_p_1_4 + C5*k_1_C_1_p_2_4 + C7*k_1_C_1_p_3_4 - C9*k_1_C_1_p_4_5 - C9*k_2_C_1_p_1_4 - C9*k_2_C_1_p_2_4 - C9*k_2_C_1_p_3_4 + C11*k_2_C_1_p_4_5 - C9*Leq*k_1_A_p_4], [C2*k_2_B_2_p_4 - C10*k_1_B_2_p_4 - C10*k_2_A_p_4 + C4*k_1_C_2_p_1_4 + C6*k_1_C_2_p_2_4 + C8*k_1_C_2_p_3_4 - C10*k_1_C_2_p_4_5 - C10*k_2_C_2_p_1_4 - C10*k_2_C_2_p_2_4 - C10*k_2_C_2_p_3_4 + C12*k_2_C_2_p_4_5 + C9*Leq*k_1_A_p_4], [C12*k_2_A_p_5 + C1*k_1_B_1_p_5 - C11*k_2_B_1_p_5 + C3*k_1_C_1_p_1_5 + C5*k_1_C_1_p_2_5 + C7*k_1_C_1_p_3_5 + C9*k_1_C_1_p_4_5 - C11*k_2_C_1_p_1_5 - C11*k_2_C_1_p_2_5 - C11*k_2_C_1_p_3_5 - C11*k_2_C_1_p_4_5 - C11*Leq*k_1_A_p_5], [C2*k_2_B_2_p_5 - C12*k_1_B_2_p_5 - C12*k_2_A_p_5 + C4*k_1_C_2_p_1_5 + C6*k_1_C_2_p_2_5 + C8*k_1_C_2_p_3_5 + C10*k_1_C_2_p_4_5 - C12*k_2_C_2_p_1_5 - C12*k_2_C_2_p_2_5 - C12*k_2_C_2_p_3_5 - C12*k_2_C_2_p_4_5 + C11*Leq*k_1_A_p_5]]) = matrix([[C3*k_2_B_1_p_1 - C1*k_1_B_1_p_2 - C1*k_1_B_1_p_3 - C1*k_1_B_1_p_4 - C1*k_1_B_1_p_5 - C1*k_1_B_1_p_1 + C5*k_2_B_1_p_2 + C7*k_2_B_1_p_3 + C9*k_2_B_1_p_4 + C11*k_2_B_1_p_5], [C4*k_1_B_2_p_1 + C6*k_1_B_2_p_2 + C8*k_1_B_2_p_3 + C10*k_1_B_2_p_4 + C12*k_1_B_2_p_5 - C2*k_2_B_2_p_1 - C2*k_2_B_2_p_2 - C2*k_2_B_2_p_3 - C2*k_2_B_2_p_4 - C2*k_2_B_2_p_5], [C4*k_2_A_p_1 + C1*k_1_B_1_p_1 - C3*k_2_B_1_p_1 - C3*k_1_C_1_p_1_2 - C3*k_1_C_1_p_1_3 - C3*k_1_C_1_p_1_4 - C3*k_1_C_1_p_1_5 + C5*k_2_C_1_p_1_2 + C7*k_2_C_1_p_1_3 + C9*k_2_C_1_p_1_4 + C11*k_2_C_1_p_1_5 - C3*Leq*k_1_A_p_1], [C2*k_2_B_2_p_1 - C4*k_1_B_2_p_1 - C4*k_2_A_p_1 - C4*k_1_C_2_p_1_2 - C4*k_1_C_2_p_1_3 - C4*k_1_C_2_p_1_4 - C4*k_1_C_2_p_1_5 + C6*k_2_C_2_p_1_2 + C8*k_2_C_2_p_1_3 + C10*k_2_C_2_p_1_4 + C12*k_2_C_2_p_1_5 + C3*Leq*k_1_A_p_1], [C6*k_2_A_p_2 + C1*k_1_B_1_p_2 - C5*k_2_B_1_p_2 + C3*k_1_C_1_p_1_2 - C5*k_1_C_1_p_2_3 - C5*k_1_C_1_p_2_4 - C5*k_1_C_1_p_2_5 - C5*k_2_C_1_p_1_2 + C7*k_2_C_1_p_2_3 + C9*k_2_C_1_p_2_4 + C11*k_2_C_1_p_2_5 - C5*Leq*k_1_A_p_2], [C2*k_2_B_2_p_2 - C6*k_1_B_2_p_2 - C6*k_2_A_p_2 + C4*k_1_C_2_p_1_2 - C6*k_1_C_2_p_2_3 - C6*k_1_C_2_p_2_4 - C6*k_1_C_2_p_2_5 - C6*k_2_C_2_p_1_2 + C8*k_2_C_2_p_2_3 + C10*k_2_C_2_p_2_4 + C12*k_2_C_2_p_2_5 + C5*Leq*k_1_A_p_2], [C8*k_2_A_p_3 + C1*k_1_B_1_p_3 - C7*k_2_B_1_p_3 + C3*k_1_C_1_p_1_3 + C5*k_1_C_1_p_2_3 - C7*k_1_C_1_p_3_4 - C7*k_1_C_1_p_3_5 - C7*k_2_C_1_p_1_3 - C7*k_2_C_1_p_2_3 + C9*k_2_C_1_p_3_4 + C11*k_2_C_1_p_3_5 - C7*Leq*k_1_A_p_3], [C2*k_2_B_2_p_3 - C8*k_1_B_2_p_3 - C8*k_2_A_p_3 + C4*k_1_C_2_p_1_3 + C6*k_1_C_2_p_2_3 - C8*k_1_C_2_p_3_4 - C8*k_1_C_2_p_3_5 - C8*k_2_C_2_p_1_3 - C8*k_2_C_2_p_2_3 + C10*k_2_C_2_p_3_4 + C12*k_2_C_2_p_3_5 + C7*Leq*k_1_A_p_3], [C10*k_2_A_p_4 + C1*k_1_B_1_p_4 - C9*k_2_B_1_p_4 + C3*k_1_C_1_p_1_4 + C5*k_1_C_1_p_2_4 + C7*k_1_C_1_p_3_4 - C9*k_1_C_1_p_4_5 - C9*k_2_C_1_p_1_4 - C9*k_2_C_1_p_2_4 - C9*k_2_C_1_p_3_4 + C11*k_2_C_1_p_4_5 - C9*Leq*k_1_A_p_4], [C2*k_2_B_2_p_4 - C10*k_1_B_2_p_4 - C10*k_2_A_p_4 + C4*k_1_C_2_p_1_4 + C6*k_1_C_2_p_2_4 + C8*k_1_C_2_p_3_4 - C10*k_1_C_2_p_4_5 - C10*k_2_C_2_p_1_4 - C10*k_2_C_2_p_2_4 - C10*k_2_C_2_p_3_4 + C12*k_2_C_2_p_4_5 + C9*Leq*k_1_A_p_4], [C12*k_2_A_p_5 + C1*k_1_B_1_p_5 - C11*k_2_B_1_p_5 + C3*k_1_C_1_p_1_5 + C5*k_1_C_1_p_2_5 + C7*k_1_C_1_p_3_5 + C9*k_1_C_1_p_4_5 - C11*k_2_C_1_p_1_5 - C11*k_2_C_1_p_2_5 - C11*k_2_C_1_p_3_5 - C11*k_2_C_1_p_4_5 - C11*Leq*k_1_A_p_5], [C2*k_2_B_2_p_5 - C12*k_1_B_2_p_5 - C12*k_2_A_p_5 + C4*k_1_C_2_p_1_5 + C6*k_1_C_2_p_2_5 + C8*k_1_C_2_p_3_5 + C10*k_1_C_2_p_4_5 - C12*k_2_C_2_p_1_5 - C12*k_2_C_2_p_2_5 - C12*k_2_C_2_p_3_5 - C12*k_2_C_2_p_4_5 + C11*Leq*k_1_A_p_5]])](5U_R_RL_images/math942.png)
![]()
Conclusion:
Typed K-matrix is correct
K matrix for the 5U-R-RL model
K;
![matrix([[- k_1_B_1_p_1 - k_1_B_1_p_2 - k_1_B_1_p_3 - k_1_B_1_p_4 - k_1_B_1_p_5, 0, k_2_B_1_p_1, 0, k_2_B_1_p_2, 0, k_2_B_1_p_3, 0, k_2_B_1_p_4, 0, k_2_B_1_p_5, 0], [0, - k_2_B_2_p_1 - k_2_B_2_p_2 - k_2_B_2_p_3 - k_2_B_2_p_4 - k_2_B_2_p_5, 0, k_1_B_2_p_1, 0, k_1_B_2_p_2, 0, k_1_B_2_p_3, 0, k_1_B_2_p_4, 0, k_1_B_2_p_5], [k_1_B_1_p_1, 0, - k_2_B_1_p_1 - k_1_C_1_p_1_2 - k_1_C_1_p_1_3 - k_1_C_1_p_1_4 - k_1_C_1_p_1_5 - Leq*k_1_A_p_1, k_2_A_p_1, k_2_C_1_p_1_2, 0, k_2_C_1_p_1_3, 0, k_2_C_1_p_1_4, 0, k_2_C_1_p_1_5, 0], [0, k_2_B_2_p_1, Leq*k_1_A_p_1, - k_2_A_p_1 - k_1_B_2_p_1 - k_1_C_2_p_1_2 - k_1_C_2_p_1_3 - k_1_C_2_p_1_4 - k_1_C_2_p_1_5, 0, k_2_C_2_p_1_2, 0, k_2_C_2_p_1_3, 0, k_2_C_2_p_1_4, 0, k_2_C_2_p_1_5], [k_1_B_1_p_2, 0, k_1_C_1_p_1_2, 0, - k_2_B_1_p_2 - k_1_C_1_p_2_3 - k_1_C_1_p_2_4 - k_1_C_1_p_2_5 - k_2_C_1_p_1_2 - Leq*k_1_A_p_2, k_2_A_p_2, k_2_C_1_p_2_3, 0, k_2_C_1_p_2_4, 0, k_2_C_1_p_2_5, 0], [0, k_2_B_2_p_2, 0, k_1_C_2_p_1_2, Leq*k_1_A_p_2, - k_2_A_p_2 - k_1_B_2_p_2 - k_1_C_2_p_2_3 - k_1_C_2_p_2_4 - k_1_C_2_p_2_5 - k_2_C_2_p_1_2, 0, k_2_C_2_p_2_3, 0, k_2_C_2_p_2_4, 0, k_2_C_2_p_2_5], [k_1_B_1_p_3, 0, k_1_C_1_p_1_3, 0, k_1_C_1_p_2_3, 0, - k_2_B_1_p_3 - k_1_C_1_p_3_4 - k_1_C_1_p_3_5 - k_2_C_1_p_1_3 - k_2_C_1_p_2_3 - Leq*k_1_A_p_3, k_2_A_p_3, k_2_C_1_p_3_4, 0, k_2_C_1_p_3_5, 0], [0, k_2_B_2_p_3, 0, k_1_C_2_p_1_3, 0, k_1_C_2_p_2_3, Leq*k_1_A_p_3, - k_2_A_p_3 - k_1_B_2_p_3 - k_1_C_2_p_3_4 - k_1_C_2_p_3_5 - k_2_C_2_p_1_3 - k_2_C_2_p_2_3, 0, k_2_C_2_p_3_4, 0, k_2_C_2_p_3_5], [k_1_B_1_p_4, 0, k_1_C_1_p_1_4, 0, k_1_C_1_p_2_4, 0, k_1_C_1_p_3_4, 0, - k_2_B_1_p_4 - k_1_C_1_p_4_5 - k_2_C_1_p_1_4 - k_2_C_1_p_2_4 - k_2_C_1_p_3_4 - Leq*k_1_A_p_4, k_2_A_p_4, k_2_C_1_p_4_5, 0], [0, k_2_B_2_p_4, 0, k_1_C_2_p_1_4, 0, k_1_C_2_p_2_4, 0, k_1_C_2_p_3_4, Leq*k_1_A_p_4, - k_2_A_p_4 - k_1_B_2_p_4 - k_1_C_2_p_4_5 - k_2_C_2_p_1_4 - k_2_C_2_p_2_4 - k_2_C_2_p_3_4, 0, k_2_C_2_p_4_5], [k_1_B_1_p_5, 0, k_1_C_1_p_1_5, 0, k_1_C_1_p_2_5, 0, k_1_C_1_p_3_5, 0, k_1_C_1_p_4_5, 0, - k_2_B_1_p_5 - k_2_C_1_p_1_5 - k_2_C_1_p_2_5 - k_2_C_1_p_3_5 - k_2_C_1_p_4_5 - Leq*k_1_A_p_5, k_2_A_p_5], [0, k_2_B_2_p_5, 0, k_1_C_2_p_1_5, 0, k_1_C_2_p_2_5, 0, k_1_C_2_p_3_5, 0, k_1_C_2_p_4_5, Leq*k_1_A_p_5, - k_2_A_p_5 - k_1_B_2_p_5 - k_2_C_2_p_1_5 - k_2_C_2_p_2_5 - k_2_C_2_p_3_5 - k_2_C_2_p_4_5]])](5U_R_RL_images/math944.png)
K matrices for nU-R-RL models were successfully developed.
NOTE: 1U-R-RL is not the same as U-R-RL but identical to U-1R-RL!