Testing the I_abcd model
The I_ab model is the simplest two-state isomerization model
Contents
close all clear all
Here you will find all figures
figures_folder='I_abcd_testing_figures';
Test Computation of Equilibrium Concentrations
Set some meaningful parameters
Rtotal=1; % Receptor concentration, M K_A_1_array=linspace(0,10,10); K_A_2=5; K_B_1=2; % Set appropriate options for the model (see model file for details) model_numeric_solver='analytical' ; model_numeric_options='n/a'; concentrations_array=[]; for counter=1:length(K_A_1_array) % compute [concentrations species_names] = equilibrium_thermodynamic_equations.I_abcd_model(... Rtotal, K_A_1_array(counter), K_A_2, K_B_1,... model_numeric_solver, model_numeric_options); % collect concentrations_array = [concentrations_array ; concentrations]; end
Plot
Figure_title= 'I_abcd model'; X_range=[0 max(K_A_1_array)+0.1 ]; % extend X just a bit past last point Y_range=[0 Rtotal ]; % keep automatic scaling for Y % display figure figure_handle=equilibrium_thermodynamic_equations.plot_populations(... K_A_1_array, concentrations_array, species_names, Figure_title, X_range, Y_range); xlabel('K_A_1','FontSize',14); % save it results_output.output_figure(figure_handle, figures_folder, 'Concentrations_plot');
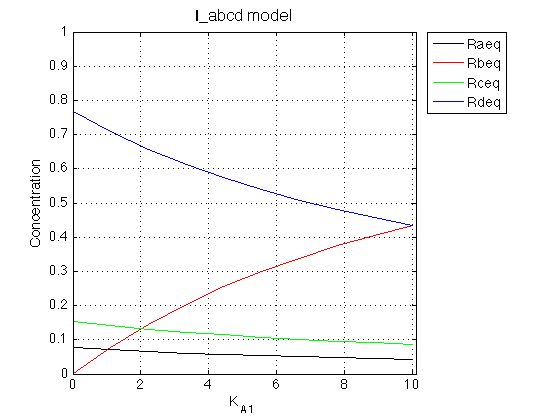
Observations
This calculation matches the result shown in IDAP/Mathematical_models/Equilibrium_thermodynamic_models/I_abcd/I_abcd_analysis.mn.
Conclusion
The model equilibrium_thermodynamic_equations.I_abcd_model() works well.
Test of NMR line shape calculations
We will generate line shapes for in conditions where we can expect specific patterns. We will plot a spectrum at a specific solution conditions (we will not use Series of datasets for simplicity).
Create NMR line shape dataset
Create data object for 1D NMR line shapes
test1=NMRLineShapes1D('Simulation','Test_1'); test1.set_active_model('I_abcd-model', model_numeric_solver, model_numeric_options) test1.show_active_model() % to look up necessary parameters of the model
ans = Active model: Model 3: "I_abcd-model" Model description "Four-state intramolecular isomerization, analytical" Model handle: line_shape_equations_1D.I_abcd_model_1D Current solver: analytical Model parameters: 1: Rtotal 2: K_A_1 3: K_A_2 4: K_B_1 5: k_2_A_1 6: k_2_A_2 7: k_2_B_1 8: k_2_B_2 9: w0_Ra 10: w0_Rb 11: w0_Rc 12: w0_Rd 13: FWHH_Ra 14: FWHH_Rb 15: FWHH_Rc 16: FWHH_Rd 17: ScaleFactor
Set range for X to extend beyond resonances, /s
w_min= -200;
w_max= 1100;
datapoints=100; % Does not matter much because smooth curve is anyway calculated
test1.set_X(linspace(w_min, w_max, datapoints));
Set fixed plotting ranges for easier comparison If we do not set ranges they will be chosen automatically for each graph
test1.X_range=[w_min w_max]; % this sets display range in the plots test1.Y_range=[0 8e-5]; % this sets display range in the plots
Calculate ideal data: set noise RMSD to 0 for both X and Y
X_RMSD=0; Y_RMSD=0;
Test 1:
test_number=1; name='Slow exchange: equal populations, equal FWHH' % Use the same thermodynamic parameters as above. Add spectral and kinetic parameters: Rtotal=1e-3; % equilibrium constants K_A_1=1; K_A_2=1; K_B_1=1; % reverse rate constant , 1/s k_2_A_1=10; k_2_A_2=10; k_2_B_1=10; k_2_B_2=10; % NMR frequencies , 1/s w0_Ra=900; w0_Rb=600; w0_Rc=300; w0_Rd=0; % line width at half height of the peak, 1/s FWHH_Ra=20; FWHH_Rb=20; FWHH_Rc=20; FWHH_Rd=20; % a multiplier for spectral amplitude (used only when fitting data) ScaleFactor=3; % compute equilbrium concentrations [concentrations species_names] = equilibrium_thermodynamic_equations.I_abcd_model(... Rtotal, K_A_1, K_A_2, K_B_1,... model_numeric_solver, model_numeric_options); % plot line shapes parameters=[ Rtotal K_A_1 K_A_2 K_B_1 k_2_A_1 k_2_A_2 k_2_B_1 k_2_B_2 w0_Ra w0_Rb w0_Rc w0_Rd FWHH_Ra FWHH_Rb FWHH_Rc FWHH_Rd ScaleFactor ]; test1.simulate_noisy_data(parameters, X_RMSD, Y_RMSD); figure_handle=test1.plot_simulation(name); results_output.output_figure(figure_handle, figures_folder, sprintf('Test_results.%d', test_number));
name = Slow exchange: equal populations, equal FWHH
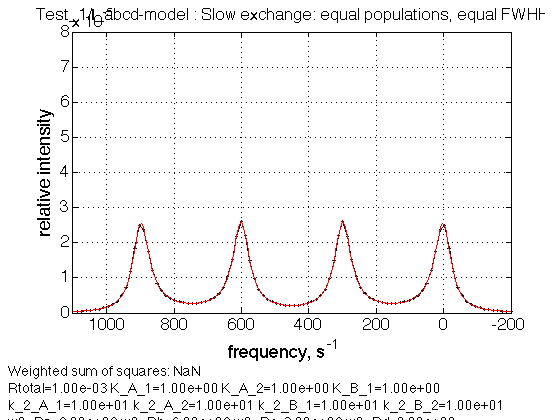
Observations
We see a correct 1:1:1:1 intensity ratio, peak positioning and the line widths
Test 2:
test_number=2; name='Fast exchange in As: equal populations, equal FWHH' % Use the same thermodynamic parameters as above. Add spectral and kinetic parameters: Rtotal=1e-3; % equilibrium constants K_A_1=1; K_A_2=1; K_B_1=1; % reverse rate constant , 1/s k_2_A_1=500; k_2_A_2=500; k_2_B_1=10; k_2_B_2=10; % NMR frequencies , 1/s w0_Ra=900; w0_Rb=600; w0_Rc=300; w0_Rd=0; % line width at half height of the peak, 1/s FWHH_Ra=20; FWHH_Rb=20; FWHH_Rc=20; FWHH_Rd=20; % a multiplier for spectral amplitude (used only when fitting data) ScaleFactor=3; % compute equilbrium concentrations [concentrations species_names] = equilibrium_thermodynamic_equations.I_abcd_model(... Rtotal, K_A_1, K_A_2, K_B_1,... model_numeric_solver, model_numeric_options); % plot line shapes parameters=[ Rtotal K_A_1 K_A_2 K_B_1 k_2_A_1 k_2_A_2 k_2_B_1 k_2_B_2 w0_Ra w0_Rb w0_Rc w0_Rd FWHH_Ra FWHH_Rb FWHH_Rc FWHH_Rd ScaleFactor ]; test1.simulate_noisy_data(parameters, X_RMSD, Y_RMSD); figure_handle=test1.plot_simulation(name); results_output.output_figure(figure_handle, figures_folder, sprintf('Test_results.%d', test_number));
name = Fast exchange in As: equal populations, equal FWHH
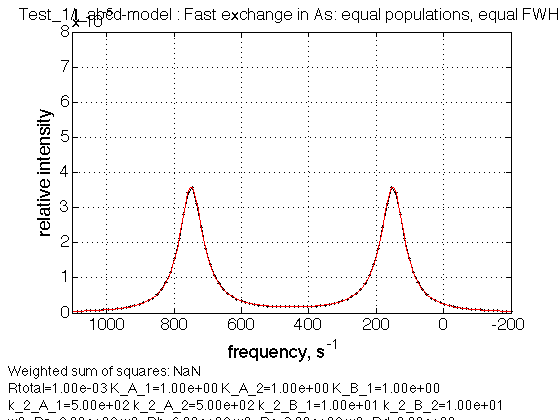
Observations
We see expected averaged a/b and c/d peaks
Test 3:
test_number=3; name='Fast exchange in Bs: equal populations, equal FWHH' % Use the same thermodynamic parameters as above. Add spectral and kinetic parameters: Rtotal=1e-3; % equilibrium constants K_A_1=1; K_A_2=1; K_B_1=1; % reverse rate constant , 1/s k_2_A_1=10; k_2_A_2=10; k_2_B_1=1000; k_2_B_2=1000; % NMR frequencies , 1/s w0_Ra=900; w0_Rb=600; w0_Rc=300; w0_Rd=0; % line width at half height of the peak, 1/s FWHH_Ra=20; FWHH_Rb=20; FWHH_Rc=20; FWHH_Rd=20; % a multiplier for spectral amplitude (used only when fitting data) ScaleFactor=3; % compute equilbrium concentrations [concentrations species_names] = equilibrium_thermodynamic_equations.I_abcd_model(... Rtotal, K_A_1, K_A_2, K_B_1,... model_numeric_solver, model_numeric_options); % plot line shapes parameters=[ Rtotal K_A_1 K_A_2 K_B_1 k_2_A_1 k_2_A_2 k_2_B_1 k_2_B_2 w0_Ra w0_Rb w0_Rc w0_Rd FWHH_Ra FWHH_Rb FWHH_Rc FWHH_Rd ScaleFactor ]; test1.simulate_noisy_data(parameters, X_RMSD, Y_RMSD); figure_handle=test1.plot_simulation(name); results_output.output_figure(figure_handle, figures_folder, sprintf('Test_results.%d', test_number));
name = Fast exchange in Bs: equal populations, equal FWHH
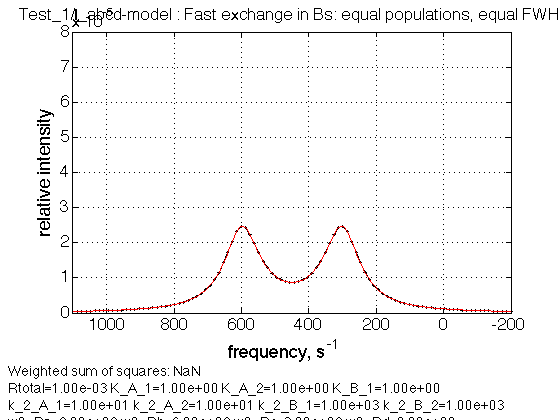
Observations
We see peaks at correct averaged positions
Test 4:
test_number=4; name='Slow exchange : equal FWHH' % Use the same thermodynamic parameters as above. Add spectral and kinetic parameters: Rtotal=1e-3; % equilibrium constants K_A_1=6; K_A_2=5; K_B_1=2; % reverse rate constant , 1/s k_2_A_1=10; k_2_A_2=10; k_2_B_1=10; k_2_B_2=10; % NMR frequencies , 1/s w0_Ra=900; w0_Rb=600; w0_Rc=300; w0_Rd=0; % line width at half height of the peak, 1/s FWHH_Ra=20; FWHH_Rb=20; FWHH_Rc=20; FWHH_Rd=20; % a multiplier for spectral amplitude (used only when fitting data) ScaleFactor=3; % compute equilbrium concentrations [concentrations species_names] = equilibrium_thermodynamic_equations.I_abcd_model(... Rtotal, K_A_1, K_A_2, K_B_1,... model_numeric_solver, model_numeric_options); % plot line shapes parameters=[ Rtotal K_A_1 K_A_2 K_B_1 k_2_A_1 k_2_A_2 k_2_B_1 k_2_B_2 w0_Ra w0_Rb w0_Rc w0_Rd FWHH_Ra FWHH_Rb FWHH_Rc FWHH_Rd ScaleFactor ]; test1.simulate_noisy_data(parameters, X_RMSD, Y_RMSD); figure_handle=test1.plot_simulation(name); results_output.output_figure(figure_handle, figures_folder, sprintf('Test_results.%d', test_number));
name = Slow exchange : equal FWHH
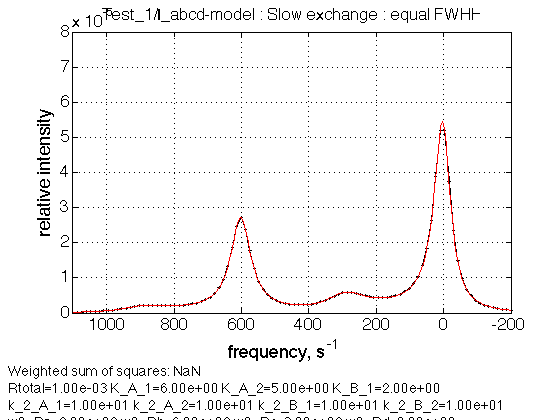
Observations
We see peaks with intensities correctly ranging according to the populations plot for K_A_1=6.
Test 5:
test_number=5; name='Slow exchange: different FWHH' % Use the same thermodynamic parameters as above. Add spectral and kinetic parameters: Rtotal=1e-3; % equilibrium constants K_A_1=1; K_A_2=1; K_B_1=1; % reverse rate constant , 1/s k_2_A_1=10; k_2_A_2=10; k_2_B_1=10; k_2_B_2=10; % NMR frequencies , 1/s w0_Ra=900; w0_Rb=600; w0_Rc=300; w0_Rd=0; % line width at half height of the peak, 1/s FWHH_Ra=20; FWHH_Rb=40; FWHH_Rc=60; FWHH_Rd=80; % a multiplier for spectral amplitude (used only when fitting data) ScaleFactor=3; % compute equilbrium concentrations [concentrations species_names] = equilibrium_thermodynamic_equations.I_abcd_model(... Rtotal, K_A_1, K_A_2, K_B_1,... model_numeric_solver, model_numeric_options); % plot line shapes parameters=[ Rtotal K_A_1 K_A_2 K_B_1 k_2_A_1 k_2_A_2 k_2_B_1 k_2_B_2 w0_Ra w0_Rb w0_Rc w0_Rd FWHH_Ra FWHH_Rb FWHH_Rc FWHH_Rd ScaleFactor ]; test1.simulate_noisy_data(parameters, X_RMSD, Y_RMSD); figure_handle=test1.plot_simulation(name); results_output.output_figure(figure_handle, figures_folder, sprintf('Test_results.%d', test_number));
name = Slow exchange: different FWHH
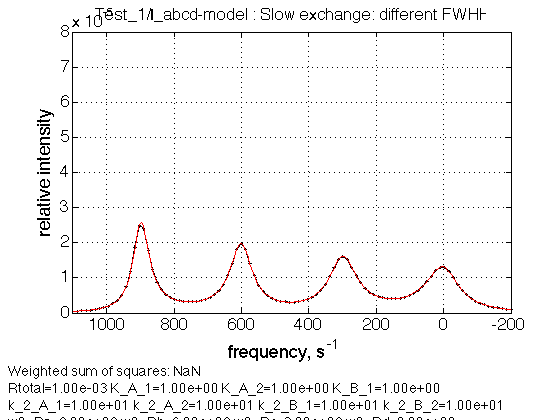
Observations
We see linewidths increasing as expected from a to d
Test 5:
test_number=5; name='Fast A2/Slow A1, B1 and B2: same FWHH' % Use the same thermodynamic parameters as above. Add spectral and kinetic parameters: Rtotal=1e-3; % equilibrium constants K_A_1=1; K_A_2=1; K_B_1=1; % reverse rate constant , 1/s k_2_A_1=10; k_2_A_2=1000; k_2_B_1=10; k_2_B_2=10; % NMR frequencies , 1/s w0_Ra=900; w0_Rb=600; w0_Rc=300; w0_Rd=0; % line width at half height of the peak, 1/s FWHH_Ra=20; FWHH_Rb=20; FWHH_Rc=20; FWHH_Rd=20; % a multiplier for spectral amplitude (used only when fitting data) ScaleFactor=3; % compute equilbrium concentrations [concentrations species_names] = equilibrium_thermodynamic_equations.I_abcd_model(... Rtotal, K_A_1, K_A_2, K_B_1,... model_numeric_solver, model_numeric_options); % plot line shapes parameters=[ Rtotal K_A_1 K_A_2 K_B_1 k_2_A_1 k_2_A_2 k_2_B_1 k_2_B_2 w0_Ra w0_Rb w0_Rc w0_Rd FWHH_Ra FWHH_Rb FWHH_Rc FWHH_Rd ScaleFactor ]; test1.simulate_noisy_data(parameters, X_RMSD, Y_RMSD); figure_handle=test1.plot_simulation(name); results_output.output_figure(figure_handle, figures_folder, sprintf('Test_results.%d', test_number));
name = Fast A2/Slow A1, B1 and B2: same FWHH
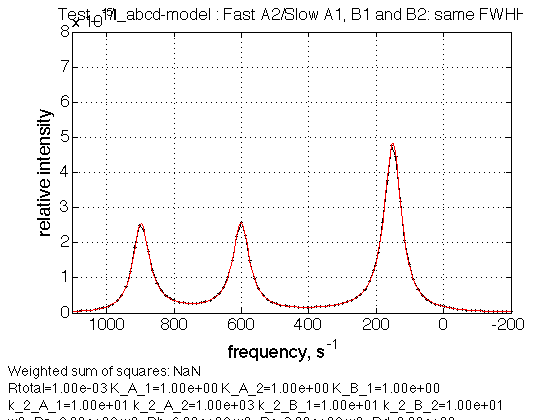
Observations
We see expected individual peaks of a and b, and averaged peak of c and d
CONCLUSIONS
The I_abcd model works correctly!