Testing of the U_L model
by Evgenii Kovrigin, 6/1/2011
Contents
close all clear all
Here you will find all figures
figures_folder='U_L_testing_figures';
TEST COMPUTATION OF EQUILIBRIUM POPULATIONS
Set some meaningful parameters
Rtotal=1e-3; % Receptor concentration, M LRratio_array=[0 : 0.02 : 1.45]; % Array of L/R K_a_A=1e6; % Binding affinity constant K_a_B=4; % Isomerization constant % Set appropriate options for the model (see model file for details) model_numeric_solver='analytical' ; model_numeric_options='none';
Compute arrays for populations and plot
concentrations_array=[]; for counter=1:length(LRratio_array) % compute [concentrations species_names] = equilibrium_thermodynamic_equations.U_L_model(... Rtotal, LRratio_array(counter), K_a_A, K_a_B,... model_numeric_solver, model_numeric_options); % collect concentrations_array = [concentrations_array ; concentrations]; end
Plot
Figure_title= 'U-L model'; X_range=[0 max(LRratio_array)+0.1 ]; % extend X just a bit past last point Y_range=[ ]; % keep automatic scaling for Y % display figure figure_handle=equilibrium_thermodynamic_equations.plot_populations(... LRratio_array, concentrations_array, species_names, Figure_title, X_range, Y_range); % save it results_output.output_figure(figure_handle, figures_folder, 'Concentrations_plot');
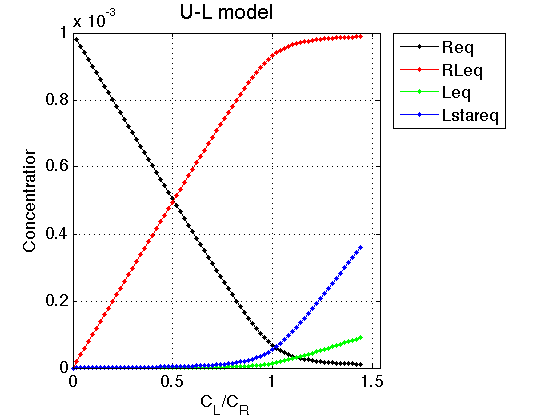
Observations The result is exactly what we expect from this model. Free ligand is split between two forms: binding-competent L and incompetent L*. As the receptor approaches saturation, amount of free ligand increases but ratio between L and L* remains constant.
Conclusion
The model equilibrium_thermodynamic_equations.U_L_model() works well.
Test of NMR line shape calculations
We will generate line shapes in conditions where we can expect specific patterns. We will plot a spectrum at a specific solution conditions (we will not use Series of datasets for simplicity).
(1) Ligand-free receptor gives one peak; (2) Saturated receptor gives one peak; (3) A titration series in slow and fast exchange
Create NMR line shape dataset
Create data object for 1D NMR line shapes
test1=NMRLineShapes1D('Simulation','Test_1'); test1.set_active_model('U_L-model', model_numeric_solver, model_numeric_options) test1.show_active_model() % to look up necessary parameters of the model
ans = Active model: Model 8: "U_L-model" Model description "1D NMR line shape for the U-L model, no temperature/field dependence, analytical" Model handle: line_shape_equations_1D.U_L_model_1D Current solver: analytical Model parameters: 1: Rtotal 2: LRratio 3: log10(K_A) 4: log10(K_B) 5: k_2_A 6: w0_R 7: w0_RL 8: FWHH_R 9: FWHH_RL 10: ScaleFactor
Set range for X to extend beyond resonances
w_min= -300;
w_max= 500;
datapoints=100; % Does not matter much because smooth curve is anyway calculated
test1.set_X(linspace(w_min, w_max, datapoints));
Set fixed plotting ranges for easier comparison If we do not set ranges they will be chosen automatically for each graph
test1.X_range=[w_min w_max]; % this sets display range in the plots test1.Y_range=[0 1e-4]; % this sets display range in the plots
Calculate ideal data: set noise RMSD to 0 for both X and Y
X_RMSD=0; Y_RMSD=0;
Free receptor
Use the same thermodynamic parameters as above. Add spectral and kinetic parameters:
LRratio = 0.001 ; Log10_K_A = log10(K_a_A); Log10_K_B = log10(K_a_B); k_2_A = 1; % dissociation rate constant of the complex, 1/s w0_R = -200; % NMR frequency of the free receptor R, 1/s w0_RL = 400; % NMR frequency of the bound complex RL, 1/s FWHH_R = 20; % line width at half height of the peak of R, 1/s FWHH_RL = 20; % line width at half height of the peak of RL, 1/s ScaleFactor = 1; % a multiplier for spectral amplitude (used only when fitting data) % compute equilbrium concentrations [concentrations species_names] = equilibrium_thermodynamic_equations.U_L_model(... Rtotal, LRratio, K_a_A, K_a_B,... model_numeric_solver, model_numeric_options) % plot line shapes parameters=[ Rtotal LRratio Log10_K_A Log10_K_B k_2_A ... w0_R w0_RL FWHH_R FWHH_RL ScaleFactor ]; test1.simulate_noisy_data(parameters, X_RMSD, Y_RMSD); figure_handle=test1.plot_simulation('Free R'); results_output.output_figure(figure_handle, figures_folder, 'Free_R');
concentrations =
1.0e-03 *
0.9990 0.0010 0.0000 0.0000
species_names =
'Req' 'RLeq' 'Leq' 'Lstareq'
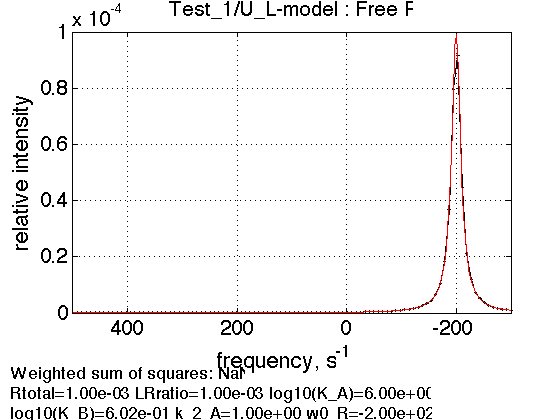
Expected peak of free R
Prepare TotalFit session for easy display of many graphs
storage_session=TotalFit('All_tests'); % set aside for plotting later storage_session.copy_dataset_into_array(test1);
Bound receptor
Use the same thermodynamic parameters as above. Add spectral and kinetic parameters:
LRratio = 10 ; % plot line shapes parameters=[ Rtotal LRratio Log10_K_A Log10_K_B k_2_A ... w0_R w0_RL FWHH_R FWHH_RL ScaleFactor ]; test1.simulate_noisy_data(parameters, X_RMSD, Y_RMSD); figure_handle=test1.plot_simulation('Bound R'); results_output.output_figure(figure_handle, figures_folder, 'Bound_R'); % set aside for plotting later storage_session.copy_dataset_into_array(test1);
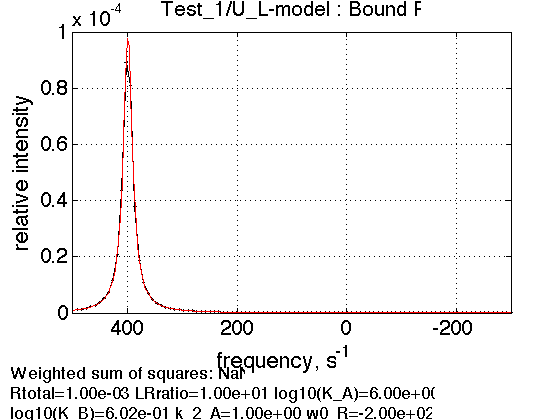
Expected peak of RL
Intermediate point: slow exchange
Use the same thermodynamic parameters as above. Add spectral and kinetic parameters:
LRratio = 0.5 ; % compute equilbrium concentrations [concentrations species_names] = equilibrium_thermodynamic_equations.U_L_model(... Rtotal, LRratio, K_a_A, K_a_B,... model_numeric_solver, model_numeric_options) % plot line shapes parameters=[ Rtotal LRratio Log10_K_A Log10_K_B k_2_A ... w0_R w0_RL FWHH_R FWHH_RL ScaleFactor ]; test1.simulate_noisy_data(parameters, X_RMSD, Y_RMSD); figure_handle=test1.plot_simulation('Slow: int.point'); results_output.output_figure(figure_handle, figures_folder, 'Slow_int_pt'); % set aside for plotting later storage_session.copy_dataset_into_array(test1);
concentrations =
1.0e-03 *
0.5049 0.4951 0.0010 0.0039
species_names =
'Req' 'RLeq' 'Leq' 'Lstareq'

Expected splitting 50-50 between bound and free forms
Intermediate point: slow exchange - really strong shift towards L*
Use the same thermodynamic parameters as above. Add spectral and kinetic parameters:
K_a_B = 700 ; Log10_K_B = log10(K_a_B); % % *Compute arrays for populations and plot* concentrations_array=[]; for counter=1:length(LRratio_array) % compute [concentrations species_names] = equilibrium_thermodynamic_equations.U_L_model(... Rtotal, LRratio_array(counter), K_a_A, K_a_B,... model_numeric_solver, model_numeric_options); % collect concentrations_array = [concentrations_array ; concentrations]; end % Plot Figure_title= 'U-L model: high KB'; X_range=[0 max(LRratio_array)+0.1 ]; % extend X just a bit past last point Y_range=[ ]; % keep automatic scaling for Y % display figure figure_handle=equilibrium_thermodynamic_equations.plot_populations(... LRratio_array, concentrations_array, species_names, Figure_title, X_range, Y_range); % save it results_output.output_figure(figure_handle, figures_folder, 'Concentrations_plot_high_KB'); % plot line shapes parameters=[ Rtotal LRratio Log10_K_A Log10_K_B k_2_A ... w0_R w0_RL FWHH_R FWHH_RL ScaleFactor ]; test1.simulate_noisy_data(parameters, X_RMSD, Y_RMSD); figure_handle=test1.plot_simulation('Slow: int.point2'); results_output.output_figure(figure_handle, figures_folder, 'Slow_int_pt2'); % set aside for plotting later storage_session.copy_dataset_into_array(test1);
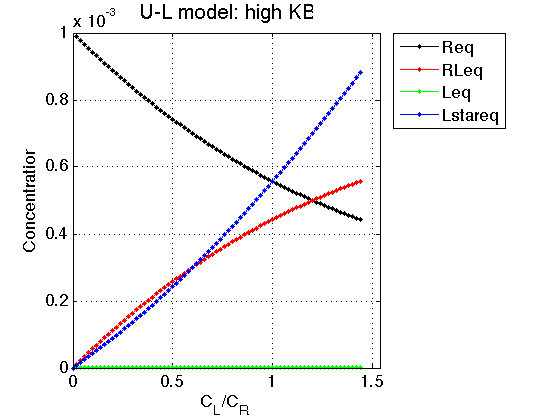
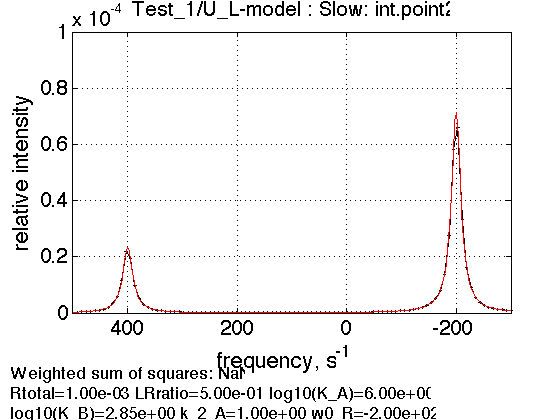
We observe that increasing shift of isomerization equilibrium in L towards non-binding L* leads to reduced saturation of R: as if binding affinity becomes weaker.
Summary of individual plots
storage_session.define_series('All-tests',1:length(storage_session.dataset_array)); figure_handle=storage_session.plot_1D_series('All-tests', 'All tests', 0); results_output.output_figure(figure_handle, figures_folder, 'All_tests');
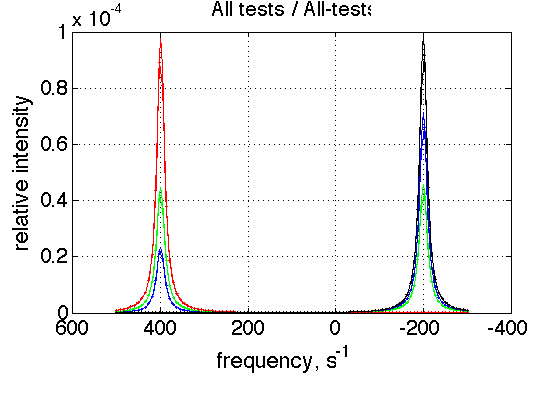
This is a comparison graph of all previous plots
Create a titration series
(see Tutorial 3 for details) Choose parameters
ZERO_LRratio= 1e-3; % This number cannot be too small---the model is numeric and will NOT converge! LRratio_vector=[ZERO_LRratio 0.2 0.4 0.6 0.8 1.0 1.2 1.4 ]; k_2_A=1000; % fast exchange K_a_B = 4 ; % weaker isomerization Log10_K_B = log10(K_a_B); % choose the same parameters as above session_name='Series'; session=TotalFit(session_name); series_name='U-L_simulation'; dataset_class_name='NMRLineShapes1D'; model_name='U_L-model'; number_of_datasets=length(LRratio_vector); X_column=test1.X; % use the same range % create TotalFit session session.create_simulation_series(series_name, dataset_class_name, model_name, ... model_numeric_solver, model_numeric_options,... number_of_datasets, X_column); session.initialize_relation_matrix(sprintf('%s.all_datasets.txt', session_name)); % link parameters parameter_number_array=[ 1 3 4 5 6 7 8 9 10 ]; session.batch_link_parameters_in_series(series_name, parameter_number_array); session.generate_fitting_environment(sprintf('%s.fitting_environment.txt', session_name)) % prepare parameters first_dataset_index=session.dataset_index(series_name,1); FAKE_VALUE=1E-6; % individual (unlinked) parameters: to be assigned later ideal_parameters=[ Rtotal FAKE_VALUE Log10_K_A Log10_K_B k_2_A ... w0_R w0_RL FWHH_R FWHH_RL ScaleFactor ]; % prepare formal limits fake_limits=zeros(1,length(ideal_parameters)); Monte_Carlo_range_min=fake_limits; Monte_Carlo_range_max=fake_limits; parameter_limits_min=fake_limits; parameter_limits_max=fake_limits; % assign session.assign_parameter_values(first_dataset_index, ideal_parameters, ... Monte_Carlo_range_min, Monte_Carlo_range_max, parameter_limits_min, parameter_limits_max); % Assign unlinked LRratio and ranges parameter_number=2; values_array=LRratio_vector; unlinked_fake_ranges=zeros(1,number_of_datasets); MonteCarlo_range_min_array=unlinked_fake_ranges; MonteCarlo_range_max_array=unlinked_fake_ranges; parameter_limits_min_array=unlinked_fake_ranges; parameter_limits_max_array=unlinked_fake_ranges; session.assign_unlinked_parameter_in_series(... series_name, parameter_number, values_array, ... MonteCarlo_range_min_array, MonteCarlo_range_max_array, ... parameter_limits_min_array, parameter_limits_max_array); % Simulate series X_standard_dev=0; Y_standard_dev=1e-8; % something really small session.simulate_series(series_name, X_standard_dev, Y_standard_dev); % Plot Y_offset_percent=10; % to offset figures vertically for easier viewing % set plotting ranges X_range=test1.X_range; % use old Y_range=[]; % automatic session.set_XY_ranges_series(series_name, X_range, Y_range) figure_handle=session.plot_1D_series(series_name, session.name, Y_offset_percent); results_output.output_figure(figure_handle, figures_folder, 'Series');
Dataset listing is written to "Series.all_datasets.txt". Fitting environment saved in Series.fitting_environment.txt. ans = New parameter relations (indexed as in all_parameters vector): [1] 1:Rtotal | 2:Rtotal | 3:Rtotal | 4:Rtotal | 5:Rtotal | 6:Rtotal | 7:Rtotal | 8:Rtotal [2] 1:LRratio [3] 1:log10(K_A) | 2:log10(K_A) | 3:log10(K_A) | 4:log10(K_A) | 5:log10(K_A) | 6:log10(K_A) | 7:log10(K_A) | 8:log10(K_A) [4] 1:log10(K_B) | 2:log10(K_B) | 3:log10(K_B) | 4:log10(K_B) | 5:log10(K_B) | 6:log10(K_B) | 7:log10(K_B) | 8:log10(K_B) [5] 1:k_2_A | 2:k_2_A | 3:k_2_A | 4:k_2_A | 5:k_2_A | 6:k_2_A | 7:k_2_A | 8:k_2_A [6] 1:w0_R | 2:w0_R | 3:w0_R | 4:w0_R | 5:w0_R | 6:w0_R | 7:w0_R | 8:w0_R [7] 1:w0_RL | 2:w0_RL | 3:w0_RL | 4:w0_RL | 5:w0_RL | 6:w0_RL | 7:w0_RL | 8:w0_RL [8] 1:FWHH_R | 2:FWHH_R | 3:FWHH_R | 4:FWHH_R | 5:FWHH_R | 6:FWHH_R | 7:FWHH_R | 8:FWHH_R [9] 1:FWHH_RL | 2:FWHH_RL | 3:FWHH_RL | 4:FWHH_RL | 5:FWHH_RL | 6:FWHH_RL | 7:FWHH_RL | 8:FWHH_RL [10] 1:ScaleFactor | 2:ScaleFactor | 3:ScaleFactor | 4:ScaleFactor | 5:ScaleFactor | 6:ScaleFactor | 7:ScaleFactor | 8:ScaleFactor [11] n/a [12] 2:LRratio [13] n/a [14] n/a [15] n/a [16] n/a [17] n/a [18] n/a [19] n/a [20] n/a [21] n/a [22] 3:LRratio [23] n/a [24] n/a [25] n/a [26] n/a [27] n/a [28] n/a [29] n/a [30] n/a [31] n/a [32] 4:LRratio [33] n/a [34] n/a [35] n/a [36] n/a [37] n/a [38] n/a [39] n/a [40] n/a [41] n/a [42] 5:LRratio [43] n/a [44] n/a [45] n/a [46] n/a [47] n/a [48] n/a [49] n/a [50] n/a [51] n/a [52] 6:LRratio [53] n/a [54] n/a [55] n/a [56] n/a [57] n/a [58] n/a [59] n/a [60] n/a [61] n/a [62] 7:LRratio [63] n/a [64] n/a [65] n/a [66] n/a [67] n/a [68] n/a [69] n/a [70] n/a [71] n/a [72] 8:LRratio [73] n/a [74] n/a [75] n/a [76] n/a [77] n/a [78] n/a [79] n/a [80] n/a Summary of datasets with lookup vectors (position of each parameter in all_parameter vector) -------- Dataset 1/U-L_simulation-1, model "U_L-model" Parameters : Rtotal LRratio log10(K_A) log10(K_B) k_2_A w0_R w0_RL FWHH_R FWHH_RL ScaleFactor Lookup vector : 1 2 3 4 5 6 7 8 9 10 Dataset 2/U-L_simulation-2, model "U_L-model" Parameters : Rtotal LRratio log10(K_A) log10(K_B) k_2_A w0_R w0_RL FWHH_R FWHH_RL ScaleFactor Lookup vector : 1 12 3 4 5 6 7 8 9 10 Dataset 3/U-L_simulation-3, model "U_L-model" Parameters : Rtotal LRratio log10(K_A) log10(K_B) k_2_A w0_R w0_RL FWHH_R FWHH_RL ScaleFactor Lookup vector : 1 22 3 4 5 6 7 8 9 10 Dataset 4/U-L_simulation-4, model "U_L-model" Parameters : Rtotal LRratio log10(K_A) log10(K_B) k_2_A w0_R w0_RL FWHH_R FWHH_RL ScaleFactor Lookup vector : 1 32 3 4 5 6 7 8 9 10 Dataset 5/U-L_simulation-5, model "U_L-model" Parameters : Rtotal LRratio log10(K_A) log10(K_B) k_2_A w0_R w0_RL FWHH_R FWHH_RL ScaleFactor Lookup vector : 1 42 3 4 5 6 7 8 9 10 Dataset 6/U-L_simulation-6, model "U_L-model" Parameters : Rtotal LRratio log10(K_A) log10(K_B) k_2_A w0_R w0_RL FWHH_R FWHH_RL ScaleFactor Lookup vector : 1 52 3 4 5 6 7 8 9 10 Dataset 7/U-L_simulation-7, model "U_L-model" Parameters : Rtotal LRratio log10(K_A) log10(K_B) k_2_A w0_R w0_RL FWHH_R FWHH_RL ScaleFactor Lookup vector : 1 62 3 4 5 6 7 8 9 10 Dataset 8/U-L_simulation-8, model "U_L-model" Parameters : Rtotal LRratio log10(K_A) log10(K_B) k_2_A w0_R w0_RL FWHH_R FWHH_RL ScaleFactor Lookup vector : 1 72 3 4 5 6 7 8 9 10
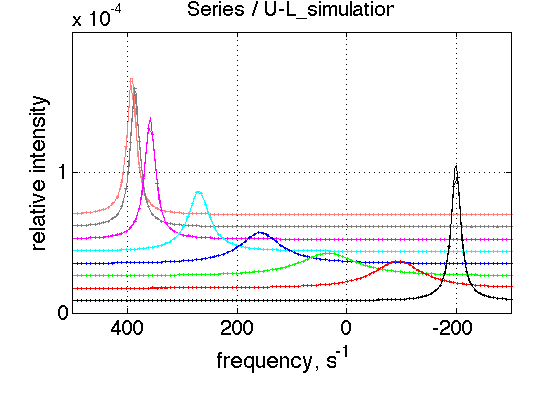
This is expected behavior for fast-intermediate regime.
Conclusions
The U-L model for NMR 1D line shapes works as expected.