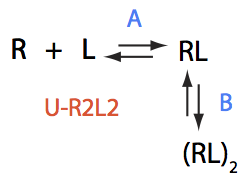
U-R2L2
Derivation of differential equations describing evolution of spin populations

1. Reaction rates and partial conversion rates
4. Expression in terms of spin (monomer) concentrations
clean up workspace
reset()
Write properly balanced reactions equations:
Transition A:
(1) (2)
R+L<=>RL
Constants: k_1_A (forward), k_2_A (reverse).
Transition B:
(1) (2)
2RL <=> (RL)2
Constants: k_1_B (forward), k_2_B (reverse).
Write reaction rates
We distinguish reaction rates ( Rate, elementary reaction acts per unit time) and conversion rates (dc/dt, number of moles of specific species consumed/produced per unit time). Conversion rates, dc/dt, for species are related to reaction rates, Rate, through molecularity coefficients.
We also distinguish here partial conversion rates from net (overall) conversion rates. The net conversion rate is actual rate of change in measured concentration of the species. Partial conversion rate is the conversion rate of the species along a specific branch of the reaction mechanism. Summing partial conversion rates of the species one obtains the net conversion rate.
Ligand binding rates (forward transition on A: 1_A)
a reaction rate
eq1_1a:=Rate_1_A = k_1_A*R*L
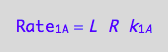
a partial conversion rate of R
eq1_1b:= dcRdt_1_A = Rate_1_A
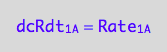
The final form
eq1_1c:= eq1_1b | eq1_1a
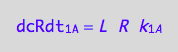
RL dissociation rates (reverse transition on A: 2_A)
a reaction rate
eq1_2a:=Rate_2_A = k_2_A*RL
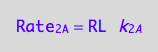
a partial conversion rate of RL
eq1_2b:= dcRLdt_2_A = Rate_2_A
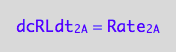
The final form
eq1_2c:= eq1_2b | eq1_2a
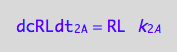
RL dimerization rates (forward transition on B: 1_B)
a reaction rate
eq1_3a:= Rate_1_B = k_1_B*RL*RL
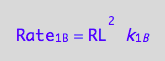
a partial conversion rate of RL
(two molecules are involved in one reaction act)
eq1_3b:= dcRLdt_1_B = 2* Rate_1_B
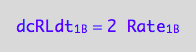
The final form
eq1_3c:= eq1_3b | eq1_3a
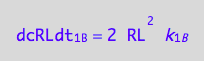
RL dimer dissociation rates (reverse transition on B: 1_B)
a reaction rate
eq1_4a:= Rate_2_B = k_2_B * R2L2
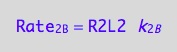
a partial conversion rate of R2
eq1_4b:= dcR2L2dt_2_B = Rate_2_B
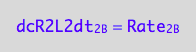
The final form
eq1_4c:= eq1_4b |eq1_4a
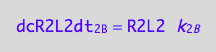
To define evolution of the species we need to compute concentrations as a function of time. To this end, we will write differential equations for conversion rates of all species.
In a reversible process both forward and reverse reaction occur simultaneously. Thus, the net conversion rate of the species is a difference between partial conversion rates resulting from forward and reverse reactions, summed along all branches.
Net conversion rate of R
Sum all pertaining partial rates with respective signs
eq3_1:= dcRdt_N = -dcRdt_1_A + dcRdt_2_A

Let's determine what the terms are.
The forward term
eq1_1c
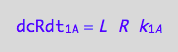
The reverse reaction on A converts one molecule of RL to one of R so
dcRdt_2_A = dcRLdt_2_A;
eq3_2:= % | eq1_2c
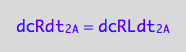
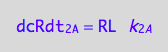
Therefore, the net conversion rate is
eq3_4:= eq3_1 | eq1_1c | eq3_2

Net conversion rate of RL
Sum all pertaining partial rates with respective signs
eq3_5:= dcRLdt_N = dcRLdt_1_A -dcRLdt_2_A - dcRLdt_1_B + dcRLdt_2_B

dissociation rate is known
eq1_2c
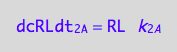
and dimerization rate:
eq1_3c
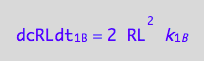
The formation rate of RL from R and L would be
dcRLdt_1_A=dcRdt_1_A;
eq3_6:= % | eq1_1c

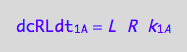
The formation rate from a dimer is double the dissociation rate of a dimer (two molecules of RL are made of one (RL)2 dissociating):
dcRLdt_2_B=2*dcR2L2dt_2_B;
eq3_7:= % | eq1_4c
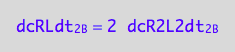
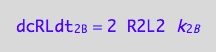
Thus, the net conversion rate
eq3_8:= eq3_5 | eq1_2c | eq1_3c | eq3_6 | eq3_7

Net conversion rate of (RL)2
Sum all pertaining partial rates with respective signs
eq3_9:= dcR2L2dt_N = dcR2L2dt_1_B - dcR2L2dt_2_B

Dissociation rate is known
eq1_4c
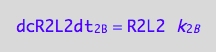
Dimerization: conversion rate of the dimer is half of the conversion rate of the monomer
dcR2L2dt_1_B= dcRLdt_1_B/2;
eq3_10:= % | eq1_3c
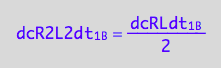
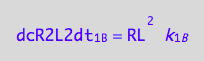
Thus, the net conversion rate of a dimer is
eq3_11:= eq3_9 | eq1_4c | eq3_10
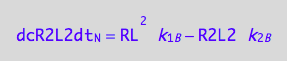
The Bloch-McConnell equations describe evolution of bulk magnetization of a sample, which is proportional to the number of spins found in every specific magnetic environment. A dimer contains two identical spins, therefore the amount of magnetization from spins in the environment of dimer is proportional to the doubled equilibrium concentration of a dimer.
Define new variables for concentrations and net conversion rates
We assign species as: R-1, RL-2, R2L2-3.
A monomeric receptor contains only one spin so everything is equivalent:
eq4_1a:= C_1 = R;
eq4_1b:= dC_1dt=dcRdt_N
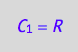

A bound complex contains one spin as well
eq4_2a:= C_2 = RL;
eq4_2b:= dC_2dt = dcRLdt_N
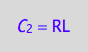

The RL dimer contains two spins
eq4_3a:= C_3 = R2L2*2;
eq4_3b:= dC_3dt = 2* dcR2L2dt_N
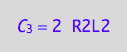

Express concentration of species in new concentration terms
solve(eq4_1a, R):
eq4_4:= R = %[1]
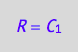
solve(eq4_2a, RL):
eq4_5:= RL = %[1]
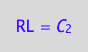
solve(eq4_3a, R2L2):
eq4_6:= R2L2 = %[1]
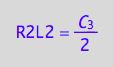
Obtain conversion rates in new concentrations
A spin in a monomeric receptor
eq4_1b | eq3_4;
eq4_7:= % | eq4_4 | eq4_5 | eq4_6

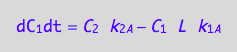
A spin in a bound complex
eq4_2b | eq3_8;
eq4_8:= % | eq4_4 | eq4_5 | eq4_6


A spin in a dimeric complex
eq4_3b | eq3_11;
eq4_9:= % | eq4_4 | eq4_5 | eq4_6
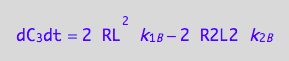
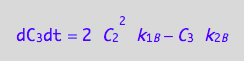
Summarize the derivation results
These are the differential equations governing concentrations of spins experiencing environment of a free receptor, C1, a monomeric receptor-ligand complex, C2, and a dimer of receptor-ligand complex, C3.
eq4_7;
eq4_8;
eq4_9;
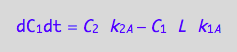

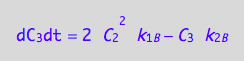
where
eq4_1a;
eq4_2a;
eq4_3a;
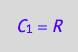
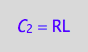
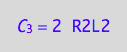
Prepare results for transfer to MATLAB
To avoid typing errors when transfering derived K matrix to MATLAB we type it in here and then directly test against derivation result. Then K matrix may be transfered to MATLAB by cut-and-paste of the MuPad output.
Restate the results
eq4_7;
eq4_8;
eq4_9;
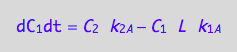

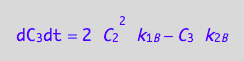
Enter the K-matrix looking at the above results.
Simple rules that allow catching mistakes in K matrix derivation:
(1) a sum of each column should be zero (so each constant must appear with both positive and negative sign), and
(2) each row has to have complete pairs of constants (i.e., if k12
appears there must be k21 in the same row with an opposite sign and so on).
K:=matrix(3,3,[
[ -L*k_1_A, k_2_A, 0 ],
[ L*k_1_A, -k_2_A-2*C_2*k_1_B, k_2_B ],
[ 0, 2*C_2*k_1_B, -k_2_B ]
])
![matrix([[-L*k_1_A, k_2_A, 0], [L*k_1_A, - k_2_A - 2*C_2*k_1_B, k_2_B], [0, 2*C_2*k_1_B, -k_2_B]])](U_R2L2_images/math54.png)
Create P-column vector
P:=matrix(3,1,[ C_1, C_2, C_3])
![matrix([[C_1], [C_2], [C_3]])](U_R2L2_images/math55.png)
Check correctness of the entered K matrix by multiplying with P and comparing to the above equations:
Multiply K and P:
dCdt_manual_input:=K*P
![matrix([[C_2*k_2_A - C_1*L*k_1_A], [C_3*k_2_B - C_2*(k_2_A + 2*C_2*k_1_B) + C_1*L*k_1_A], [2*C_2^2*k_1_B - C_3*k_2_B]])](U_R2L2_images/math56.png)
Collect right-hand-side parts of equations
dCdt_mupad:=matrix(3,1,[ rhs(eq4_7), rhs(eq4_8), rhs(eq4_9)])
![matrix([[C_2*k_2_A - C_1*L*k_1_A], [- 2*k_1_B*C_2^2 - k_2_A*C_2 + C_3*k_2_B + C_1*L*k_1_A], [2*C_2^2*k_1_B - C_3*k_2_B]])](U_R2L2_images/math57.png)
Compare derivation result to manual input
dCdt_mupad=dCdt_manual_input:
normal(%);
bool(%)
![matrix([[C_2*k_2_A - C_1*L*k_1_A], [- 2*k_1_B*C_2^2 - k_2_A*C_2 + C_3*k_2_B + C_1*L*k_1_A], [2*C_2^2*k_1_B - C_3*k_2_B]]) = matrix([[C_2*k_2_A - C_1*L*k_1_A], [- 2*k_1_B*C_2^2 - k_2_A*C_2 + C_3*k_2_B + C_1*L*k_1_A], [2*C_2^2*k_1_B - C_3*k_2_B]])](U_R2L2_images/math58.png)

=> Typed K-matrix is correct.
Use this K-matrix (copy-paste output to MATLAB)
K;
![matrix([[-L*k_1_A, k_2_A, 0], [L*k_1_A, - k_2_A - 2*C_2*k_1_B, k_2_B], [0, 2*C_2*k_1_B, -k_2_B]])](U_R2L2_images/math60.png)
Differential equations governing spin populations in U-R2L2 system have been derived. The K matrix has been prepared for transferring to MATLAB.