Testing of the U_RL model
Evgenii Kovrigin, 6/1/2011
Contents
- TEST COMPUTATION OF EQUILIBRIUM POPULATIONS
- Set some meaningful parameters
- Compute arrays for populations and plot
- TEST OF NMR LINE SHAPE CALCULATION
- Create NMR line shape dataset
- 1. Free receptor in slow exchange
- 2. Titration midpoint, slow exchange
- 3. Titration end point, slow exchange
- Summary of individual plots
- TITRATION SERIES
- CHANGE EXCHANGE REGIME IN INDIVIDUAL TRANSITIONS
- FAST A1
- FAST A2
- FAST B1
- FAST B2
- FAST As
- FAST Bs
- CONCLUSION
close all clear all
Here you will find all figures
figures_folder='U_R_RL_testing_figures';
TEST COMPUTATION OF EQUILIBRIUM POPULATIONS
Set some meaningful parameters
Rtotal=1e-3; % Receptor concentration, M LRratio_array=[0 : 0.02 : 1.45]; % Array of L/R
Set some meaningful parameters
Rtotal=1e-3; % Receptor concentration, M LRratio_array=[0 : 0.02 : 1.45]; % Array of L/R K_A_1=1e6; % Binding affinity constant K_B_1=4; % Isomerization constant K_B_2=0.5; % Isomerization constant
Dependent constant:
K_A_2 = (K_A_1*K_B_2)/K_B_1 % eq 3.2 % Set appropriate options for the model (see model file for details) model_numeric_solver='analytical' ; model_numeric_options='none';
K_A_2 =
125000
Compute arrays for populations and plot
concentrations_array=[]; for counter=1:length(LRratio_array) % compute [concentrations species_names] = equilibrium_thermodynamic_equations.U_R_RL_model(... Rtotal, LRratio_array(counter), K_A_1, K_B_1, K_B_2,... model_numeric_solver, model_numeric_options); % collect concentrations_array = [concentrations_array ; concentrations]; end
Plot
Figure_title= 'U-R-RL model'; X_range=[0 max(LRratio_array)+0.1 ]; % extend X just a bit past last point Y_range=[ 0 Rtotal]; % keep automatic scaling for Y % display figure figure_handle=equilibrium_thermodynamic_equations.plot_populations(... LRratio_array, concentrations_array, species_names, Figure_title, X_range, Y_range); % save it results_output.output_figure(figure_handle, figures_folder, 'Concentrations_plot');
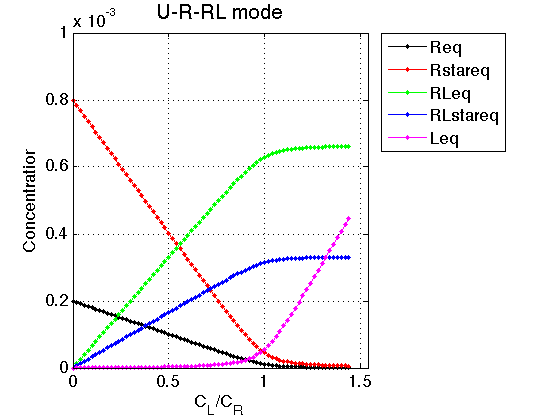
Good. Continue to line shapes.
TEST OF NMR LINE SHAPE CALCULATION
We will generate line shapes in conditions where we can expect specific patterns. We will plot a spectrum at a specific solution conditions 1. Set slow exchange and observe redistribution of populations 2. Set fast exchange for one transition at a time
Create NMR line shape dataset
Create data object for 1D NMR line shapes
test1=NMRLineShapes1D('Simulation','U-R-RL test'); test1.set_active_model('U_R_RL-model', model_numeric_solver, model_numeric_options) test1.show_active_model() % to look up necessary parameters of the model
ans = Active model: Model 12: "U_R_RL-model" Model description "1D NMR line shape for the U-R-RL model, no temperature/field dependence, analytical" Model handle: line_shape_equations_1D.U_R_RL_model_1D Current solver: analytical Model parameters: 1: Rtotal 2: LRratio 3: log10(K_A1) 4: log10(K_B1) 5: log10(K_B2) 6: k_2_A1 7: k_2_A2 8: k_2_B1 9: k_2_B2 10: w0_R 11: w0_Rstar 12: w0_RL 13: w0_RLstar 14: FWHH_R 15: FWHH_Rstar 16: FWHH_RL 17: FWHH_RLstar 18: ScaleFactor
Set range for X to extend beyond resonances
w_min= 6400; w_max= 6600; datapoints=100; % Does not matter much because smooth curve is anyway calculated test1.set_X(linspace(w_min, w_max, datapoints)); test1.X_range=[w_min w_max]; % this sets display range in the plots test1.Y_range=[0 2e-4]; % this sets display range in the plots
Calculate ideal data: set noise RMSD to 0 for both X and Y
X_RMSD=0; Y_RMSD=0;
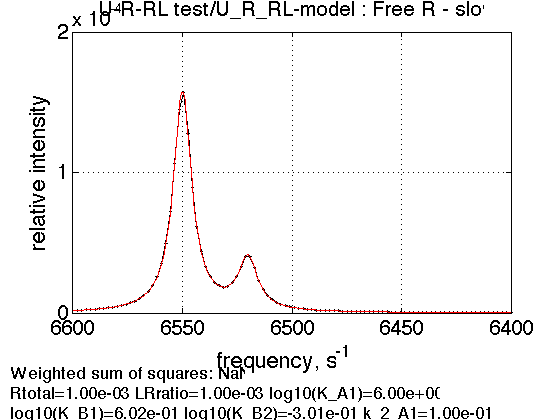
1. Free receptor in slow exchange
Use the same thermodynamic parameters as above. Add spectral and kinetic parameters:
LRratio = 0.001 ; Log10_K_A_1 = log10(K_A_1); Log10_K_B_1 = log10(K_B_1); Log10_K_B_2 = log10(K_B_2); k_2_A_1 = 0.1; % dissociation rate constant of RL, 1/s k_2_A_2 = 0.1; % dissociation rate constant of RL*, 1/s k_2_B_1 = 0.1; % isomerization rate constant, 1/s k_2_B_2 = 0.1; % isomerization rate constant, 1/s w0_R = 6520; % NMR frequency of the free receptor R, 1/s w0_Rstar = 6550; % NMR frequency of the free receptor R, 1/s w0_RL = 6480; % NMR frequency of the dimer R2, 1/s w0_RLstar = 6430; % NMR frequency of the bound complex RL, 1/s FWHH_R = 10; % line width at half height of the peak of R, 1/s FWHH_Rstar = 10; % line width at half height of the peak of R, 1/s FWHH_RL = 20; % line width at half height of the peak of R2, 1/s FWHH_RLstar = 20; % line width at half height of the peak of RL, 1/s ScaleFactor = 1; % a multiplier for spectral amplitude (used only when fitting data) % compute equilbrium concentrations [concentrations species_names] = equilibrium_thermodynamic_equations.U_R_RL_model(... Rtotal, LRratio, K_A_1, K_B_1, K_B_2,... model_numeric_solver, model_numeric_options) % plot line shapes parameters=[ Rtotal LRratio ... Log10_K_A_1 Log10_K_B_1 Log10_K_B_2 ... k_2_A_1 k_2_A_2 k_2_B_1 k_2_B_2 ... w0_R w0_Rstar w0_RL w0_RLstar ... FWHH_R FWHH_Rstar FWHH_RL FWHH_RLstar ... ScaleFactor ]; test1.simulate_noisy_data(parameters, X_RMSD, Y_RMSD); figure_handle=test1.plot_simulation('Free R - slow'); results_output.output_figure(figure_handle, figures_folder, 'Free_R_slow');
concentrations =
1.0e-03 *
0.1998 0.7992 0.0007 0.0003 0.0000
species_names =
'Req' 'Rstareq' 'RLeq' 'RLstareq' 'Leq'
Prepare TotalFit session for easy display of many graphs
storage_session=TotalFit('All_tests'); % set aside for plotting later storage_session.copy_dataset_into_array(test1);
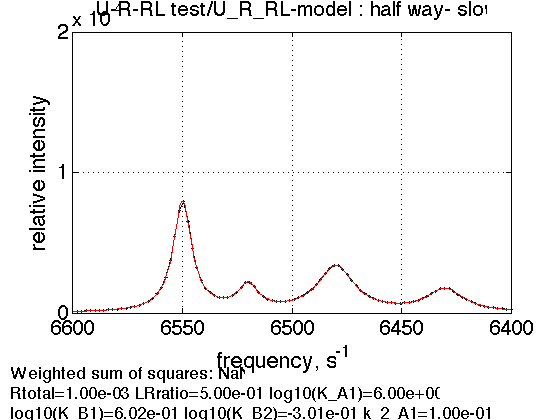
2. Titration midpoint, slow exchange
LRratio = 0.5 ; % compute equilbrium concentrations [concentrations species_names] = equilibrium_thermodynamic_equations.U_R_RL_model(... Rtotal, LRratio, K_A_1, K_B_1, K_B_2,... model_numeric_solver, model_numeric_options) % plot line shapes parameters=[ Rtotal LRratio ... Log10_K_A_1 Log10_K_B_1 Log10_K_B_2 ... k_2_A_1 k_2_A_2 k_2_B_1 k_2_B_2 ... w0_R w0_Rstar w0_RL w0_RLstar ... FWHH_R FWHH_Rstar FWHH_RL FWHH_RLstar ... ScaleFactor ]; test1.simulate_noisy_data(parameters, X_RMSD, Y_RMSD); figure_handle=test1.plot_simulation('half way- slow'); results_output.output_figure(figure_handle, figures_folder, 'Half_way_slow'); storage_session.copy_dataset_into_array(test1);
concentrations =
1.0e-03 *
0.1007 0.4026 0.3311 0.1656 0.0033
species_names =
'Req' 'Rstareq' 'RLeq' 'RLstareq' 'Leq'
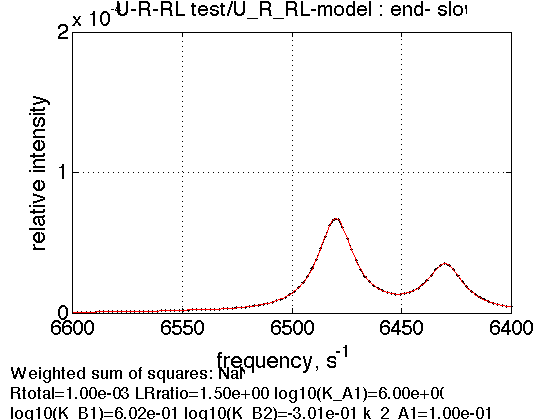
3. Titration end point, slow exchange
LRratio = 1.5 ; % compute equilbrium concentrations [concentrations species_names] = equilibrium_thermodynamic_equations.U_R_RL_model(... Rtotal, LRratio, K_A_1, K_B_1, K_B_2,... model_numeric_solver, model_numeric_options) % plot line shapes parameters=[ Rtotal LRratio ... Log10_K_A_1 Log10_K_B_1 Log10_K_B_2 ... k_2_A_1 k_2_A_2 k_2_B_1 k_2_B_2 ... w0_R w0_Rstar w0_RL w0_RLstar ... FWHH_R FWHH_Rstar FWHH_RL FWHH_RLstar ... ScaleFactor ]; test1.simulate_noisy_data(parameters, X_RMSD, Y_RMSD); figure_handle=test1.plot_simulation('end- slow'); results_output.output_figure(figure_handle, figures_folder, 'End_slow'); storage_session.copy_dataset_into_array(test1);
concentrations =
1.0e-03 *
0.0013 0.0052 0.6623 0.3312 0.5065
species_names =
'Req' 'Rstareq' 'RLeq' 'RLstareq' 'Leq'
Summary of individual plots
storage_session.define_series('All-tests',1:length(storage_session.dataset_array)); figure_handle=storage_session.plot_1D_series('All-tests', 'All tests', 0); results_output.output_figure(figure_handle, figures_folder, 'All_tests');
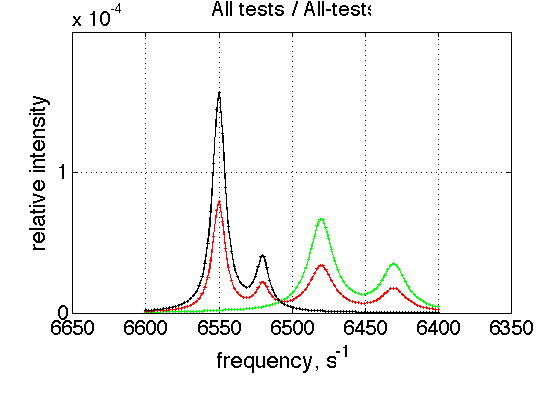
This is a comparison graph of all previous plots
TITRATION SERIES
(see Tutorial 3 for details) Choose parameters
ZERO_LRratio= 1e-3; % This number should not be zero LRratio_vector=[ZERO_LRratio 0.2 0.4 0.6 0.8 1.0 1.2 1.4 ]; % choose the same parameters as above session_name='All slow'; session=TotalFit(session_name); series_name='U-R-RL_simulation'; dataset_class_name='NMRLineShapes1D'; model_name='U_R_RL-model'; number_of_datasets=length(LRratio_vector); X_column=test1.X; % use the same range % create TotalFit session session.create_simulation_series(series_name, dataset_class_name, model_name, ... model_numeric_solver, model_numeric_options,... number_of_datasets, X_column); session.initialize_relation_matrix(sprintf('%s.all_datasets.txt', session_name)); % link parameters parameter_number_array=[ 1 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18]; session.batch_link_parameters_in_series(series_name, parameter_number_array); session.generate_fitting_environment(sprintf('%s.fitting_environment.txt', session_name)) % prepare parameters first_dataset_index=session.dataset_index(series_name,1); FAKE_VALUE=1E-6; % individual (unlinked) parameters: to be assigned later ideal_parameters=[ Rtotal FAKE_VALUE ... Log10_K_A_1 Log10_K_B_1 Log10_K_B_2... k_2_A_1 k_2_A_2 k_2_B_1 k_2_B_2 ... w0_R w0_Rstar w0_RL w0_RLstar ... FWHH_R FWHH_Rstar FWHH_RL FWHH_RLstar ScaleFactor ]; % prepare formal limits fake_limits=zeros(1,length(ideal_parameters)); Monte_Carlo_range_min=fake_limits; Monte_Carlo_range_max=fake_limits; parameter_limits_min=fake_limits; parameter_limits_max=fake_limits; % assign session.assign_parameter_values(first_dataset_index, ideal_parameters, ... Monte_Carlo_range_min, Monte_Carlo_range_max, parameter_limits_min, parameter_limits_max); % Assign unlinked LRratio and ranges parameter_number=2; values_array=LRratio_vector; unlinked_fake_ranges=zeros(1,number_of_datasets); MonteCarlo_range_min_array=unlinked_fake_ranges; MonteCarlo_range_max_array=unlinked_fake_ranges; parameter_limits_min_array=unlinked_fake_ranges; parameter_limits_max_array=unlinked_fake_ranges; session.assign_unlinked_parameter_in_series(... series_name, parameter_number, values_array, ... MonteCarlo_range_min_array, MonteCarlo_range_max_array, ... parameter_limits_min_array, parameter_limits_max_array); % Simulate series X_standard_dev=0; Y_standard_dev=1e-8; % something really small session.simulate_series(series_name, X_standard_dev, Y_standard_dev); % Plot Y_offset_percent=10; % to offset figures vertically for easier viewing % set plotting ranges X_range=test1.X_range; % use old Y_range=[]; % automatic session.set_XY_ranges_series(series_name, X_range, Y_range) figure_handle=session.plot_1D_series(series_name, session.name, Y_offset_percent); results_output.output_figure(figure_handle, figures_folder, session_name);
Dataset listing is written to "All slow.all_datasets.txt". Fitting environment saved in All slow.fitting_environment.txt. ans = New parameter relations (indexed as in all_parameters vector): [1] 1:Rtotal | 2:Rtotal | 3:Rtotal | 4:Rtotal | 5:Rtotal | 6:Rtotal | 7:Rtotal | 8:Rtotal [2] 1:LRratio [3] 1:log10(K_A1) | 2:log10(K_A1) | 3:log10(K_A1) | 4:log10(K_A1) | 5:log10(K_A1) | 6:log10(K_A1) | 7:log10(K_A1) | 8:log10(K_A1) [4] 1:log10(K_B1) | 2:log10(K_B1) | 3:log10(K_B1) | 4:log10(K_B1) | 5:log10(K_B1) | 6:log10(K_B1) | 7:log10(K_B1) | 8:log10(K_B1) [5] 1:log10(K_B2) | 2:log10(K_B2) | 3:log10(K_B2) | 4:log10(K_B2) | 5:log10(K_B2) | 6:log10(K_B2) | 7:log10(K_B2) | 8:log10(K_B2) [6] 1:k_2_A1 | 2:k_2_A1 | 3:k_2_A1 | 4:k_2_A1 | 5:k_2_A1 | 6:k_2_A1 | 7:k_2_A1 | 8:k_2_A1 [7] 1:k_2_A2 | 2:k_2_A2 | 3:k_2_A2 | 4:k_2_A2 | 5:k_2_A2 | 6:k_2_A2 | 7:k_2_A2 | 8:k_2_A2 [8] 1:k_2_B1 | 2:k_2_B1 | 3:k_2_B1 | 4:k_2_B1 | 5:k_2_B1 | 6:k_2_B1 | 7:k_2_B1 | 8:k_2_B1 [9] 1:k_2_B2 | 2:k_2_B2 | 3:k_2_B2 | 4:k_2_B2 | 5:k_2_B2 | 6:k_2_B2 | 7:k_2_B2 | 8:k_2_B2 [10] 1:w0_R | 2:w0_R | 3:w0_R | 4:w0_R | 5:w0_R | 6:w0_R | 7:w0_R | 8:w0_R [11] 1:w0_Rstar | 2:w0_Rstar | 3:w0_Rstar | 4:w0_Rstar | 5:w0_Rstar | 6:w0_Rstar | 7:w0_Rstar | 8:w0_Rstar [12] 1:w0_RL | 2:w0_RL | 3:w0_RL | 4:w0_RL | 5:w0_RL | 6:w0_RL | 7:w0_RL | 8:w0_RL [13] 1:w0_RLstar | 2:w0_RLstar | 3:w0_RLstar | 4:w0_RLstar | 5:w0_RLstar | 6:w0_RLstar | 7:w0_RLstar | 8:w0_RLstar [14] 1:FWHH_R | 2:FWHH_R | 3:FWHH_R | 4:FWHH_R | 5:FWHH_R | 6:FWHH_R | 7:FWHH_R | 8:FWHH_R [15] 1:FWHH_Rstar | 2:FWHH_Rstar | 3:FWHH_Rstar | 4:FWHH_Rstar | 5:FWHH_Rstar | 6:FWHH_Rstar | 7:FWHH_Rstar | 8:FWHH_Rstar [16] 1:FWHH_RL | 2:FWHH_RL | 3:FWHH_RL | 4:FWHH_RL | 5:FWHH_RL | 6:FWHH_RL | 7:FWHH_RL | 8:FWHH_RL [17] 1:FWHH_RLstar | 2:FWHH_RLstar | 3:FWHH_RLstar | 4:FWHH_RLstar | 5:FWHH_RLstar | 6:FWHH_RLstar | 7:FWHH_RLstar | 8:FWHH_RLstar [18] 1:ScaleFactor | 2:ScaleFactor | 3:ScaleFactor | 4:ScaleFactor | 5:ScaleFactor | 6:ScaleFactor | 7:ScaleFactor | 8:ScaleFactor [19] n/a [20] 2:LRratio [21] n/a [22] n/a [23] n/a [24] n/a [25] n/a [26] n/a [27] n/a [28] n/a [29] n/a [30] n/a [31] n/a [32] n/a [33] n/a [34] n/a [35] n/a [36] n/a [37] n/a [38] 3:LRratio [39] n/a [40] n/a [41] n/a [42] n/a [43] n/a [44] n/a [45] n/a [46] n/a [47] n/a [48] n/a [49] n/a [50] n/a [51] n/a [52] n/a [53] n/a [54] n/a [55] n/a [56] 4:LRratio [57] n/a [58] n/a [59] n/a [60] n/a [61] n/a [62] n/a [63] n/a [64] n/a [65] n/a [66] n/a [67] n/a [68] n/a [69] n/a [70] n/a [71] n/a [72] n/a [73] n/a [74] 5:LRratio [75] n/a [76] n/a [77] n/a [78] n/a [79] n/a [80] n/a [81] n/a [82] n/a [83] n/a [84] n/a [85] n/a [86] n/a [87] n/a [88] n/a [89] n/a [90] n/a [91] n/a [92] 6:LRratio [93] n/a [94] n/a [95] n/a [96] n/a [97] n/a [98] n/a [99] n/a [100] n/a [101] n/a [102] n/a [103] n/a [104] n/a [105] n/a [106] n/a [107] n/a [108] n/a [109] n/a [110] 7:LRratio [111] n/a [112] n/a [113] n/a [114] n/a [115] n/a [116] n/a [117] n/a [118] n/a [119] n/a [120] n/a [121] n/a [122] n/a [123] n/a [124] n/a [125] n/a [126] n/a [127] n/a [128] 8:LRratio [129] n/a [130] n/a [131] n/a [132] n/a [133] n/a [134] n/a [135] n/a [136] n/a [137] n/a [138] n/a [139] n/a [140] n/a [141] n/a [142] n/a [143] n/a [144] n/a Summary of datasets with lookup vectors (position of each parameter in all_parameter vector) -------- Dataset 1/U-R-RL_simulation-1, model "U_R_RL-model" Parameters : Rtotal LRratio log10(K_A1) log10(K_B1) log10(K_B2) k_2_A1 k_2_A2 k_2_B1 k_2_B2 w0_R w0_Rstar w0_RL w0_RLstar FWHH_R FWHH_Rstar FWHH_RL FWHH_RLstar ScaleFactor Lookup vector : 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 Dataset 2/U-R-RL_simulation-2, model "U_R_RL-model" Parameters : Rtotal LRratio log10(K_A1) log10(K_B1) log10(K_B2) k_2_A1 k_2_A2 k_2_B1 k_2_B2 w0_R w0_Rstar w0_RL w0_RLstar FWHH_R FWHH_Rstar FWHH_RL FWHH_RLstar ScaleFactor Lookup vector : 1 20 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 Dataset 3/U-R-RL_simulation-3, model "U_R_RL-model" Parameters : Rtotal LRratio log10(K_A1) log10(K_B1) log10(K_B2) k_2_A1 k_2_A2 k_2_B1 k_2_B2 w0_R w0_Rstar w0_RL w0_RLstar FWHH_R FWHH_Rstar FWHH_RL FWHH_RLstar ScaleFactor Lookup vector : 1 38 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 Dataset 4/U-R-RL_simulation-4, model "U_R_RL-model" Parameters : Rtotal LRratio log10(K_A1) log10(K_B1) log10(K_B2) k_2_A1 k_2_A2 k_2_B1 k_2_B2 w0_R w0_Rstar w0_RL w0_RLstar FWHH_R FWHH_Rstar FWHH_RL FWHH_RLstar ScaleFactor Lookup vector : 1 56 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 Dataset 5/U-R-RL_simulation-5, model "U_R_RL-model" Parameters : Rtotal LRratio log10(K_A1) log10(K_B1) log10(K_B2) k_2_A1 k_2_A2 k_2_B1 k_2_B2 w0_R w0_Rstar w0_RL w0_RLstar FWHH_R FWHH_Rstar FWHH_RL FWHH_RLstar ScaleFactor Lookup vector : 1 74 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 Dataset 6/U-R-RL_simulation-6, model "U_R_RL-model" Parameters : Rtotal LRratio log10(K_A1) log10(K_B1) log10(K_B2) k_2_A1 k_2_A2 k_2_B1 k_2_B2 w0_R w0_Rstar w0_RL w0_RLstar FWHH_R FWHH_Rstar FWHH_RL FWHH_RLstar ScaleFactor Lookup vector : 1 92 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 Dataset 7/U-R-RL_simulation-7, model "U_R_RL-model" Parameters : Rtotal LRratio log10(K_A1) log10(K_B1) log10(K_B2) k_2_A1 k_2_A2 k_2_B1 k_2_B2 w0_R w0_Rstar w0_RL w0_RLstar FWHH_R FWHH_Rstar FWHH_RL FWHH_RLstar ScaleFactor Lookup vector : 1 110 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 Dataset 8/U-R-RL_simulation-8, model "U_R_RL-model" Parameters : Rtotal LRratio log10(K_A1) log10(K_B1) log10(K_B2) k_2_A1 k_2_A2 k_2_B1 k_2_B2 w0_R w0_Rstar w0_RL w0_RLstar FWHH_R FWHH_Rstar FWHH_RL FWHH_RLstar ScaleFactor Lookup vector : 1 128 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18
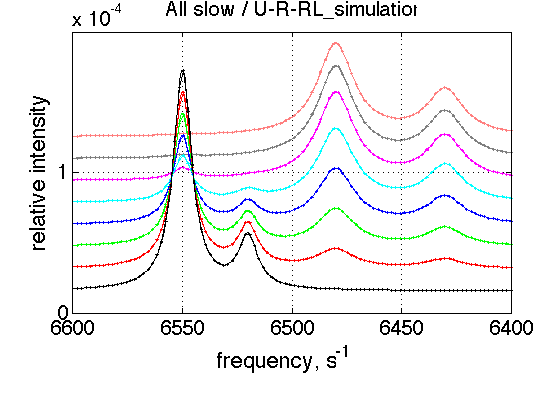
Expected result
CHANGE EXCHANGE REGIME IN INDIVIDUAL TRANSITIONS
FAST A1
simulation_name='Fast-A1'; old_value=k_2_A_1; % save it k_2_A_1=5000; % Simulate session.set_name(simulation_name); ideal_parameters=[ Rtotal FAKE_VALUE ... Log10_K_A_1 Log10_K_B_1 Log10_K_B_2... k_2_A_1 k_2_A_2 k_2_B_1 k_2_B_2 ... w0_R w0_Rstar w0_RL w0_RLstar ... FWHH_R FWHH_Rstar FWHH_RL FWHH_RLstar ScaleFactor ]; session.assign_parameter_values(first_dataset_index, ideal_parameters, ... Monte_Carlo_range_min, Monte_Carlo_range_max, parameter_limits_min, parameter_limits_max); session.simulate_series(series_name, X_standard_dev, Y_standard_dev); session.set_XY_ranges_series(series_name, X_range, Y_range) figure_handle=session.plot_1D_series(series_name, session.name, Y_offset_percent); results_output.output_figure(figure_handle, figures_folder, simulation_name); % restore value k_2_A_1=old_value;
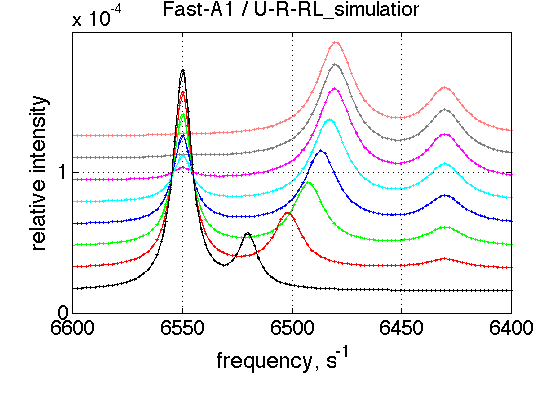
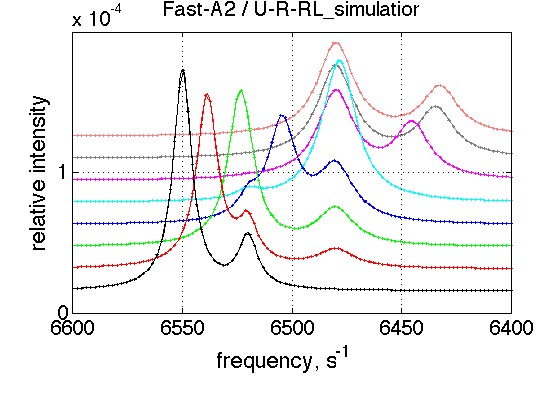
FAST A2
simulation_name='Fast-A2'; old_value=k_2_A_2; % save it k_2_A_2=5000; % Simulate session.set_name(simulation_name); ideal_parameters=[ Rtotal FAKE_VALUE ... Log10_K_A_1 Log10_K_B_1 Log10_K_B_2... k_2_A_1 k_2_A_2 k_2_B_1 k_2_B_2 ... w0_R w0_Rstar w0_RL w0_RLstar ... FWHH_R FWHH_Rstar FWHH_RL FWHH_RLstar ScaleFactor ]; session.assign_parameter_values(first_dataset_index, ideal_parameters, ... Monte_Carlo_range_min, Monte_Carlo_range_max, parameter_limits_min, parameter_limits_max); session.simulate_series(series_name, X_standard_dev, Y_standard_dev); session.set_XY_ranges_series(series_name, X_range, Y_range) figure_handle=session.plot_1D_series(series_name, session.name, Y_offset_percent); results_output.output_figure(figure_handle, figures_folder, simulation_name); % restore value k_2_A_2=old_value;
FAST B1
simulation_name='Fast-B1'; old_value=k_2_B_1; % save it k_2_B_1=5000; % Simulate session.set_name(simulation_name); ideal_parameters=[ Rtotal FAKE_VALUE ... Log10_K_A_1 Log10_K_B_1 Log10_K_B_2... k_2_A_1 k_2_A_2 k_2_B_1 k_2_B_2 ... w0_R w0_Rstar w0_RL w0_RLstar ... FWHH_R FWHH_Rstar FWHH_RL FWHH_RLstar ScaleFactor ]; session.assign_parameter_values(first_dataset_index, ideal_parameters, ... Monte_Carlo_range_min, Monte_Carlo_range_max, parameter_limits_min, parameter_limits_max); session.simulate_series(series_name, X_standard_dev, Y_standard_dev); session.set_XY_ranges_series(series_name, X_range, Y_range) figure_handle=session.plot_1D_series(series_name, session.name, Y_offset_percent); results_output.output_figure(figure_handle, figures_folder, simulation_name); % restore value k_2_B_1=old_value;
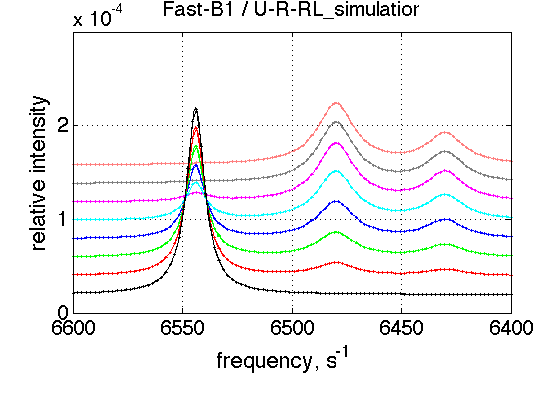
FAST B2
simulation_name='Fast-B2'; old_value=k_2_B_2; % save it k_2_B_2=5000; % Simulate session.set_name(simulation_name); ideal_parameters=[ Rtotal FAKE_VALUE ... Log10_K_A_1 Log10_K_B_1 Log10_K_B_2... k_2_A_1 k_2_A_2 k_2_B_1 k_2_B_2 ... w0_R w0_Rstar w0_RL w0_RLstar ... FWHH_R FWHH_Rstar FWHH_RL FWHH_RLstar ScaleFactor ]; session.assign_parameter_values(first_dataset_index, ideal_parameters, ... Monte_Carlo_range_min, Monte_Carlo_range_max, parameter_limits_min, parameter_limits_max); session.simulate_series(series_name, X_standard_dev, Y_standard_dev); session.set_XY_ranges_series(series_name, X_range, Y_range) figure_handle=session.plot_1D_series(series_name, session.name, Y_offset_percent); results_output.output_figure(figure_handle, figures_folder, simulation_name); % restore value k_2_B_2=old_value;
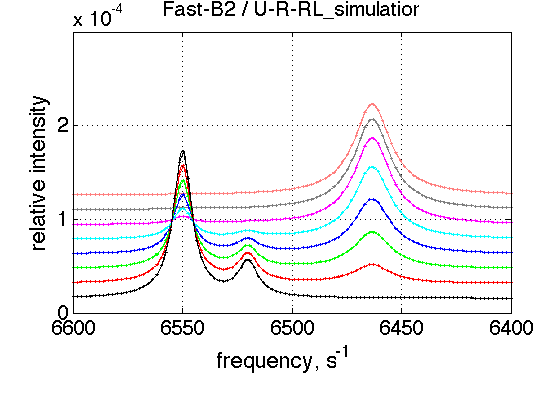
FAST As
simulation_name='Fast-A1-A2'; old_value1=k_2_A_1; % save it old_value2=k_2_A_2; % save it k_2_A_1=5000; k_2_A_2=5000; % Simulate session.set_name(simulation_name); ideal_parameters=[ Rtotal FAKE_VALUE ... Log10_K_A_1 Log10_K_B_1 Log10_K_B_2... k_2_A_1 k_2_A_2 k_2_B_1 k_2_B_2 ... w0_R w0_Rstar w0_RL w0_RLstar ... FWHH_R FWHH_Rstar FWHH_RL FWHH_RLstar ScaleFactor ]; session.assign_parameter_values(first_dataset_index, ideal_parameters, ... Monte_Carlo_range_min, Monte_Carlo_range_max, parameter_limits_min, parameter_limits_max); session.simulate_series(series_name, X_standard_dev, Y_standard_dev); session.set_XY_ranges_series(series_name, X_range, Y_range) figure_handle=session.plot_1D_series(series_name, session.name, Y_offset_percent); results_output.output_figure(figure_handle, figures_folder, simulation_name); % restore value k_2_A_1=old_value1; k_2_A_2=old_value2;
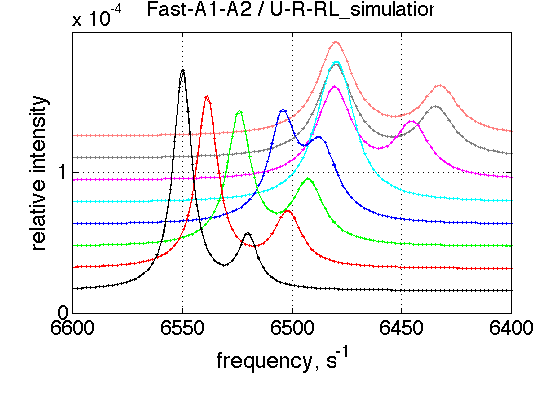
FAST Bs
simulation_name='Fast-B1-B2'; old_value1=k_2_B_1; % save it old_value2=k_2_B_2; % save it k_2_B_1=5000; k_2_B_2=5000; % Simulate session.set_name(simulation_name); ideal_parameters=[ Rtotal FAKE_VALUE ... Log10_K_A_1 Log10_K_B_1 Log10_K_B_2... k_2_A_1 k_2_A_2 k_2_B_1 k_2_B_2 ... w0_R w0_Rstar w0_RL w0_RLstar ... FWHH_R FWHH_Rstar FWHH_RL FWHH_RLstar ScaleFactor ]; session.assign_parameter_values(first_dataset_index, ideal_parameters, ... Monte_Carlo_range_min, Monte_Carlo_range_max, parameter_limits_min, parameter_limits_max); session.simulate_series(series_name, X_standard_dev, Y_standard_dev); session.set_XY_ranges_series(series_name, X_range, Y_range) figure_handle=session.plot_1D_series(series_name, session.name, Y_offset_percent); results_output.output_figure(figure_handle, figures_folder, simulation_name); % restore value k_2_B_1=old_value1; k_2_B_2=old_value2;
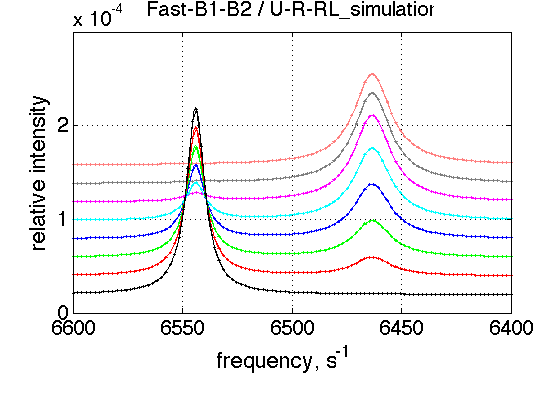
CONCLUSION
The U-R-RL model seems working fine.