Back to LineShapeKin Simulation Tutorial

U-R-RL-RM
Binding of two mutually exclusive ligands coupled with
intramolecular isomerization of the receptor
(competitive ligand binding)

U-R-RL-RM_model.pdf

This is a competitive binding mechanism. The way we simulate this system with the two ligands is that we perform titration with L while the concentration of M is set to a constant. One may also think about this model as simulating behavior of the receptor that is partially saturated with a competitive contaminating ligand M (for example, incomplete purification after extraction from the cells).

You you need to simulate titration with M: simply exchange the labels between L and M and correspondingly change the constants in the model.

NOTE: Calculation of populations of species is relatively slow due to complexity of the equations, which are  solved numerically. If you need to speed up the calculations - reduce number of points on smooth curves for populations graph (LRpoints in the general setup file setup_implementation_test.txt)

Location: U_R_RL_RM/

Contents

• Case 1: Reduce the mechanism to R+L=RL

  ---

• Case 2: Reduce the model to U-R-RL: isomerization in the receptor but no M binding occurs

  ---

• Case 3: M better binds to R*, L better binds to R, tight L, weak M binding, all in slow exchange

  ---

• Case 4: M better binds to R*, L better binds to R, tight L, weak M binding with fast off-rate of M

  ---

• Conclusions

Case 1: Reduce the mechanism to R+L=RL

Isomerization does not occur, M does not bind to R. We set M concentration to 0.6 of total R concentration for this test.

Simulate setup_implementation_test U_R_RL_RM_test1

Report: summary_report

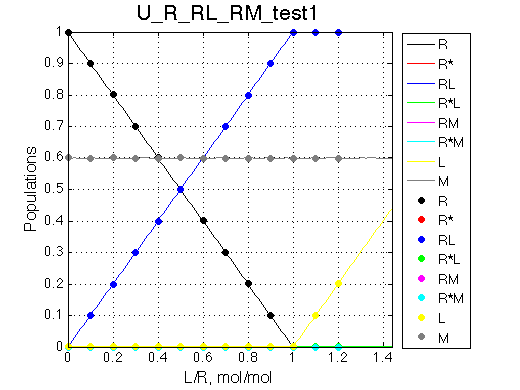
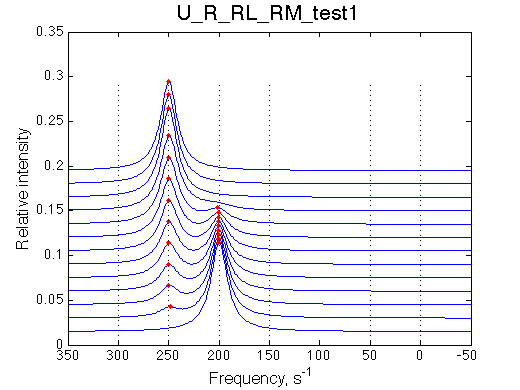
As expected, M does not bind and its population in the solution does not change.

Back to Contents

Case 2: Reduce the model to U-R-RL: isomerization in the receptor but no M binding occurs

Here we remove portion of the mechanism involving species containing M.

Simulate setup_implementation_test U_R_RL_RM_test2

Report: summary_report

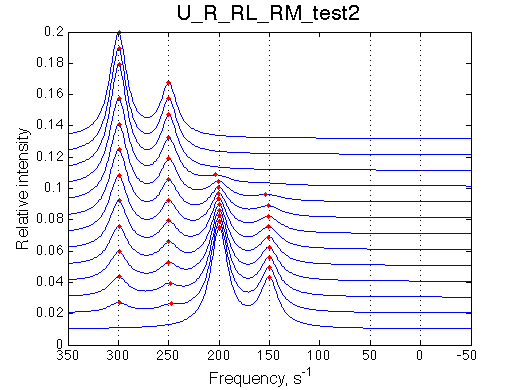
Model behaves as expected: addition of L shifts isomerization equilibrium in R. Concentration of M remains unchanged.

Back to Contents

Case 3: M better binds to R*, L better binds to R, tight L, weak M binding, all in slow exchange

Simulate setup_implementation_test U_R_RL_RM_test3

Report: summary_report

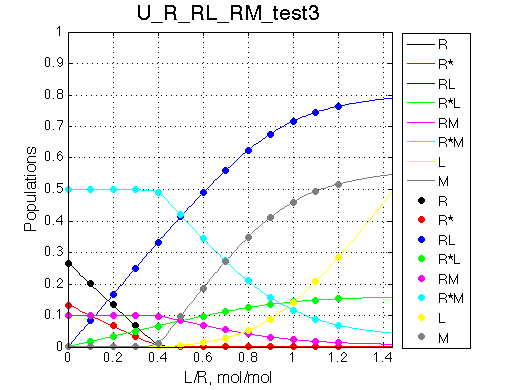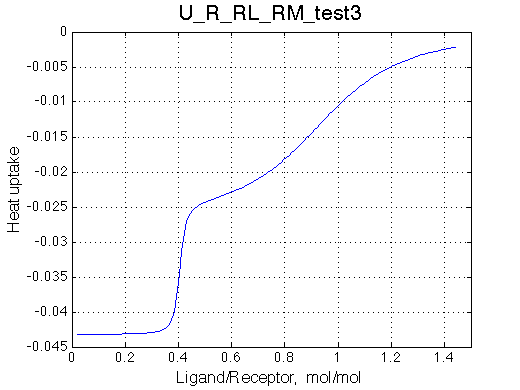Species chemical shifts (left to right on the graph):          R*L    RL   R    R*       RM    R*M

Looks right.

Back to Contents

Case 4: M better binds to R*, L better binds to R, tight L, weak M binding with fast off-rate of M

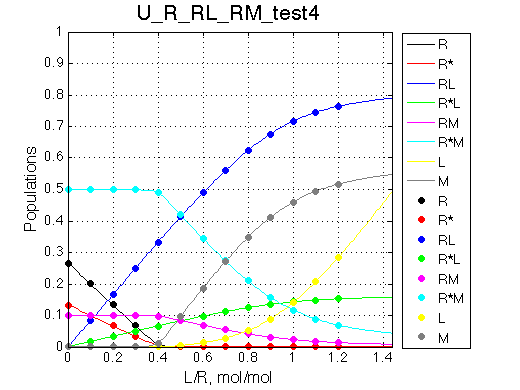
Here we are setting fast exchange regime between R and R* species, as well as between RM-R*M species.

Simulate setup_implementation_test U_R_RL_RM_test4

Report: summary_report

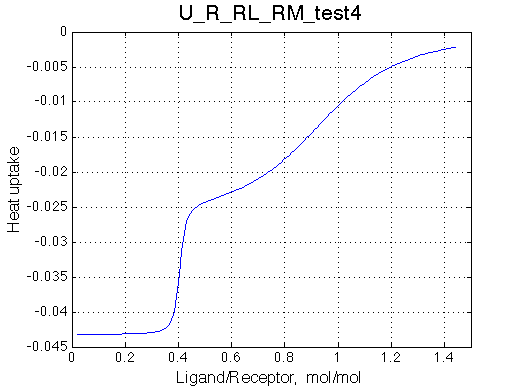Species chemical shifts (left to right on the graph):            R*L    RL   R    R*     RM    R*M

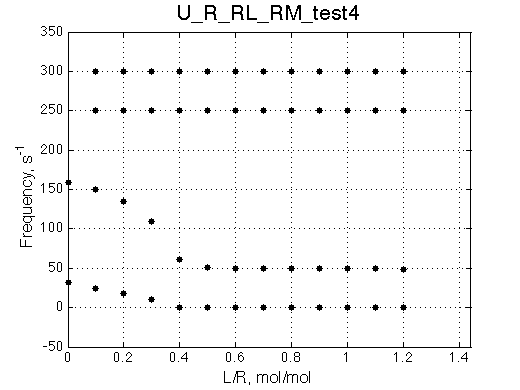To understand what is happening with the line shapes let's discuss origin of the individual peaks.

In the absence of ligand L:

• By our model parameter we have R (200 s^-1 ) in fast exchange with RM (50 s^-1 ) with an off-rate constant k_2A3=1000 s^-1 . Ratio between RM and R populations at L/R=0 is about 1:3 as can be read from the population graph, therefore we observe a weighted average peak at about 160 s^-1.

  ---

• Similarly, we have set   k_2A4=1000 s^-1 as an off-rate for R*M complex formation. Population ratio at L/R=0 for R*M to R* is approximately 5:1. Therefore the position of the average peak of R* (150 s^-1) and R*M (0 s^-1) is about 30 s^-1 .

  ---

Once we added L we see appearance of the resonances for RL (250s^-1) and R*L (300s^-1) in slow exchange. As titration progresses the RL and R*L species accumulate maintaining the constant ratio set by K_B2 =0.2.

With addition of L the fast exchange average resonances of R-RM and R*-R*M experience the following peculiar changes:

1. R-RM fast-exchange averaged peak loses intensity and shifts the position of chemical shift of RM.  The population graph shows that population of RM (pink curve) remains constant until the free receptor (black curve) is depleted. Therefore RM/R continuously increases causing a peak shift to a position of the pure RM (50s^-1) at L/R=1-MRratio=0.4 where free receptor is no longer present in significant population.

   ---

2. Further addition of L leads to displacement of M (gray curve) from RM complex reducing population of RM (pink) and its corresponding peak intensity. Peak position remains constant at the chemical shift of RM because no significant population of R is present any more.

   ---

3. R*-R*M fast-exchange peak shifts to the position of R*M for similar reasons. R*M population (cyan) remains constant while R* (red) is depleted. However, intensity of this peak remains almost the same because contribution from disappearing R* (red) is small relatively to popultion of R*M. Once L/R=1-MRratio=0.4 is reached the population of R*M begins to decrease leading to reduction in the peak intensity with fixed position.

Complex models with multiple binding/isomerization equilbria are capable of producing very sophisticated looking spectral patterns. However, using the reasoning described above one may always rationalize complex spectral patterns.

Back to Contents

Conclusions

The model works as expected.

Back to Contents

Back to LineShapeKin Simulation Tutorial