B_family_models_derivation

B family models (derivation)

Binding of two ligand molecules to one receptor monomer including bidentate

ligand binding; macroscopic and microscopic consideration.

Evgenii L. Kovrigin

12-10-2014

Updates:

1/13/2015 - rename transitions to have internal isomerization ("hopping") transition called "B" in all models and bi-dentate binding transition called "C"

Contents

Goals

1. Definitions

2. Basic equilibrium equations

3. Analysis of statistical effects on binding and kinetic constants

4. Derivation of equations for concentrations of species

5. Prepare equations for a numeric solution

6. Save results on disk for future use

Conclusions

Back to Contents

Goals

1. define thermodynamic and kinetic equations for binding of two ligands to one receptor molecule model.

2. analyze relationship between microscopic and macroscopic constants.

3. prepare equations for calculations of equilibrium concentrations in the titration experiment.

Derivation of kinetic matrices for microscopic models is done separately in Mathematical_models/NMR_line_shape_models/1D

Analysis of the solutions will be done separately.

Back to Contents

1. Definitions

clean up workspace

reset()

Set path to save results into:

NOTE: make sure the path ends with slash character "/".

ProjectName:="B_family_models_derivation";
CurrentPath:="/Volumes/Leopard_Partition/Users/kovrigin/Documents/Workspace/Global Analysis/IDAP/Mathematical_models/Equilibrium_thermodynamic_models/B_family_models/";

We will be considering the system two ways: using macroscopic and microscopic binding constants [1]. Overall, these are two completely equivalent treatments but interpretation in terms of mechanistic events is only available for microscopic constants.

1. Cantor, C.R. and Schimmel, P.R., Biophysical Chemistry. Part III. The behavior of biological macromolecules. Vol. III. 1980, New York: W.H. Freeman and Co. 360.

From: Equilibrium_thermodynamic_models/B_family_models/B

The more complicated version where the ligand is bidentate and capable of binding at both sites:

From Equilibrium_thermodynamic_models/B_family_models/B-bidentateL

This may be viewed as a combination of B and U-RL model (not exactly, though, because there are three isomerization transitions in B-bidentateL-micro.

1/13/2015:

Name replacement schedule:

B_1_I_I -> C_I_I

B_1_I -> C_I

B_1 -> B

B_2 -> B

Binding and isomerization constants

NOTE 1: All binding constants I am using are association constants.

NOTE 2: These relationships serve as restraints for solve(), but not restrict these values in calculations!

Macroscopic equilibrium constants

K_A_1

K_A_1 ;
assumeAlso(K_A_1 > 0):
assumeAlso(K_A_1 , R_):

K_A_2

K_A_2 ;
assumeAlso(K_A_2 > 0):
assumeAlso(K_A_2 , R_):

Macroscopic kinetic constants

k_1_A_1

k_1_A_1 ;
assumeAlso(k_1_A_1 > 0):
assumeAlso(k_1_A_1 , R_):

k_2_A_1

k_2_A_1 ;
assumeAlso(k_2_A_1 > 0):
assumeAlso(k_2_A_1 , R_):

k_1_A_2

k_1_A_2 ;
assumeAlso(k_1_A_2 > 0):
assumeAlso(k_1_A_2 , R_):

k_2_A_2

k_2_A_2 ;
assumeAlso(k_2_A_2 > 0):
assumeAlso(k_2_A_2 , R_):

Microscopic equilibrium binding constants

K_A_1_I

K_A_1_I ;
assumeAlso(K_A_1_I > 0):
assumeAlso(K_A_1_I , R_):

K_A_1_I_I

K_A_1_I_I ;
assumeAlso(K_A_1_I_I > 0):
assumeAlso(K_A_1_I_I , R_):

K_A_2_I

K_A_2_I ;
assumeAlso(K_A_2_I > 0):
assumeAlso(K_A_2_I , R_):

K_A_2_I_I

K_A_2_I_I ;
assumeAlso(K_A_2_I_I > 0):
assumeAlso(K_A_2_I_I , R_):

Microscopic equilibrium isomerization constants

K_C_I

K_C_I ;
assumeAlso(K_C_I > 0):
assumeAlso(K_C_I , R_):

K_C_I_I

K_C_I_I ;
assumeAlso(K_C_I_I > 0):
assumeAlso(K_C_I_I , R_):

K_B

K_B ;
assumeAlso(K_B > 0):
assumeAlso(K_B , R_):

Microscopic binding/dissociation rate constants

k_1_A_1_I

k_1_A_1_I ;
assumeAlso(k_1_A_1_I > 0):
assumeAlso(k_1_A_1_I , R_):

k_2_A_1_I

k_2_A_1_I ;
assumeAlso(k_2_A_1_I > 0):
assumeAlso(k_2_A_1_I , R_):

k_1_A_1_I_I

k_1_A_1_I_I ;
assumeAlso(k_1_A_1_I_I > 0):
assumeAlso(k_1_A_1_I_I , R_):

k_2_A_1_I_I

k_2_A_1_I_I ;
assumeAlso(k_2_A_1_I_I > 0):
assumeAlso(k_2_A_1_I_I , R_):

k_1_A_2_I_I

k_1_A_2_I_I ;
assumeAlso(k_1_A_2_I_I > 0):
assumeAlso(k_1_A_2_I_I , R_):

k_2_A_2_I_I

k_2_A_2_I_I ;
assumeAlso(k_2_A_2_I_I > 0):
assumeAlso(k_2_A_2_I_I , R_):

k_1_A_2_I

k_1_A_2_I ;
assumeAlso(k_1_A_2_I > 0):
assumeAlso(k_1_A_2_I , R_):

k_2_A_2_I

k_2_A_2_I ;
assumeAlso(k_2_A_2_I > 0):
assumeAlso(k_2_A_2_I , R_):

Microscopic isomerization rate constants

k_1_C_I_I

k_1_C_I_I ;
assumeAlso(k_1_C_I_I > 0):
assumeAlso(k_1_C_I_I , R_):

k_2_C_I_I

k_2_C_I_I ;
assumeAlso(k_2_C_I_I > 0):
assumeAlso(k_2_C_I_I , R_):

k_1_C_I

k_1_C_I ;
assumeAlso(k_1_C_I > 0):
assumeAlso(k_1_C_I , R_):

k_2_C_I

k_2_C_I ;
assumeAlso(k_2_C_I > 0):
assumeAlso(k_2_C_I , R_):

k_1_B

k_1_B ;
assumeAlso(k_1_B > 0):
assumeAlso(k_1_B , R_):

k_2_B

k_2_B ;
assumeAlso(k_2_B > 0):
assumeAlso(k_2_B , R_):

Total concentrations

Rtot - total concentration of the receptor

Rtot;
assumeAlso(Rtot>0):
assumeAlso(Rtot,R_):

Ltot - total concentration of a ligand

Ltot;
assumeAlso(Ltot>0):
assumeAlso(Ltot,R_):

Equilibrium concentrations

Req - free receptor

Req;
assumeAlso(Req>0):
assumeAlso(Req<Rtot):
assumeAlso(Req,R_):

Leq - free ligand

Leq;
assumeAlso(Leq>0):
assumeAlso(Leq<Ltot):
assumeAlso(Leq,R_):

RLeq - equlibrium conentration of single-bound species in the mAcroscopic view

(all of them summed together; they are indistinguishable in this view)

RLeq;
assumeAlso(RLeq>0):
assumeAlso(RLeq<Rtot):
assumeAlso(RLeq<Ltot):
assumeAlso(RLeq,R_):

RL_2eq - double bound species

RL_2eq;
assumeAlso(RL_2eq>0):
assumeAlso(RL_2eq<Rtot):
assumeAlso(RL_2eq<Ltot/2):
assumeAlso(RL_2eq,R_):

Microscopic equilibrium concentrations

(in this view we can independently measure their concentrations)

RL_Ieq

RL_Ieq;
assumeAlso(RL_Ieq>0):
assumeAlso(RL_Ieq<Rtot):
assumeAlso(RL_Ieq<Ltot):
assumeAlso(RL_Ieq,R_):

RL_I_Ieq

RL_I_Ieq;
assumeAlso(RL_I_Ieq>0):
assumeAlso(RL_I_Ieq<Rtot):
assumeAlso(RL_I_Ieq<Ltot):
assumeAlso(RL_I_Ieq,R_):

RL_b_ieq

RL_b_ieq;
assumeAlso(RL_b_ieq>0):
assumeAlso(RL_b_ieq<Rtot):
assumeAlso(RL_b_ieq<Ltot):
assumeAlso(RL_b_ieq,R_):

Check if all names are correctly entered:

anames(Properties,User);

${K_A_1, K_A_2, K_B, K_A_1_I, K_A_2_I, K_A_1_I_I, K_A_2_I_I, K_C_I, K_C_I_I, Leq, Ltot, RL_2eq, RL_Ieq, RL_I_Ieq, RL_b_ieq, RLeq, Req, Rtot, k_1_B, k_2_B, k_1_A_1, k_1_A_2, k_2_A_1, k_2_A_2, k_1_C_I, k_2_C_I, k_1_A_1_I, k_1_A_2_I, k_2_A_1_I, k_2_A_2_I, k_1_C_I_I, k_2_C_I_I, k_1_A_1_I_I, k_1_A_2_I_I, k_2_A_1_I_I, k_2_A_2_I_I}$

Back to Contents

2. Basic equilibrium equations

Goal: I will try to express analytical [L] from equation for a total concentration of a receptor or use the expression for a numeric solution if analytical is not possible

2.1 Equations for the mAcroscopic B model

Total concentration (mass balance) equations:

eq2_1_1_BmAcro:= Rtot = Req + RLeq + RL_2eq;
eq2_1_2_BmAcro:= Ltot = Leq + RLeq + 2* RL_2eq

Equilibrium thermodynamics equations for independent constants

eq2_1_3_BmAcro:= K_A_1 = RLeq / (Req*Leq);

K_A_1 = RLeq/(Leq*Req)

eq2_1_4_BmAcro:= K_A_2 = RL_2eq / (RLeq*Leq);

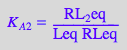
K_A_2 = RL_2eq/(Leq*RLeq)

2.2 Equations for the microscopic B model (mono-dentate binding only)

Total concentration (mass balance) equations:

eq2_2_1_Bmicro:= RLeq = RL_Ieq + RL_I_Ieq;

eq2_2_2_Bmicro:= Rtot = Req + RLeq + RL_2eq;

eq2_2_3_Bmicro:= Ltot = Leq + RLeq + 2* RL_2eq;

Equilibrium thermodynamics equations for independent constants:

eq2_2_4_Bmicro:= K_A_1_I = RL_Ieq / (Req*Leq);

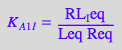
K_A_1_I = RL_Ieq/(Leq*Req)

eq2_2_5_Bmicro:= K_A_1_I_I = RL_I_Ieq / (Req*Leq);

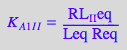
K_A_1_I_I = RL_I_Ieq/(Leq*Req)

eq2_2_6_Bmicro:= K_A_2_I_I = RL_2eq / (RL_Ieq*Leq);

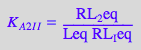
K_A_2_I_I = RL_2eq/(Leq*RL_Ieq)

Dependent constants: K_A_2_I and K_B (from thermodynamic cycles)

eq2_2_7_Bmicro:= K_A_2_I = K_A_1_I * K_A_2_I_I / K_A_1_I_I

eq2_2_8_Bmicro:= K_B = K_A_1_I_I / K_A_1_I

2.3 Equations for the microscopic B-bidentateL model (bi-dentate ligand)

Total concentration (mass balance) equations:

eq2_3_1_Bbidentate:= RLeq = RL_Ieq + RL_I_Ieq + RL_b_ieq;

eq2_3_2_Bbidentate:= Rtot = Req + RLeq + RL_2eq;

eq2_3_3_Bbidentate:= Ltot = Leq + RLeq + 2*RL_2eq;

Equilibrium thermodynamics equations for independent constants:

eq2_3_4_Bbidentate:= K_A_1_I = RL_Ieq / (Req*Leq);

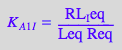
K_A_1_I = RL_Ieq/(Leq*Req)

eq2_3_5_Bbidentate:= K_A_1_I_I = RL_I_Ieq / (Req*Leq);

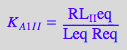
K_A_1_I_I = RL_I_Ieq/(Leq*Req)

eq2_3_6_Bbidentate:= K_A_2_I_I = RL_2eq / (RL_Ieq*Leq);

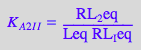
K_A_2_I_I = RL_2eq/(Leq*RL_Ieq)

eq2_3_7_Bbidentate:= K_C_I_I = RL_b_ieq / (RL_Ieq);

K_C_I_I = RL_b_ieq/RL_Ieq

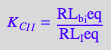
Dependent: K_A_2_I, K_C_I, and K_B (from thermodynamic cycles)

eq2_3_8_Bbidentate:= K_A_2_I = K_A_1_I * K_A_2_I_I / K_A_1_I_I

eq2_3_9_Bbidentate:= K_C_I = K_A_1_I * K_C_I_I / K_A_1_I_I

eq2_3_10_Bbidentate:= K_B = K_A_1_I_I / K_A_1_I

Back to Contents

3. Analysis of statistical effects on binding and kinetic constants

"Statistical effects" implies differences between macroscopic and microscopic constants due to the fact that in the macroscopic view we cannot discriminate individual single-bound species [1]. Standard approach: express equilbrium concentrations of those species you will not discriminate in the macroscopic treatment ("microscopic species") and then substitute into the mass balance equation for the single-bound species. Then substitute the result into the macroscopic association constant expression.

[1]. Cantor, C.R. and Schimmel, P.R., Biophysical Chemistry. Part III. The behavior of biological macromolecules. Vol. III. 1980, New York: W.H. Freeman and Co. 360.

3.1 Microscopic B model (mono-dentate ligand binding)

Mass balance

eq2_2_1_Bmicro

Macroscopic steps

eq2_1_3_BmAcro

K_A_1 = RLeq/(Leq*Req)

eq2_1_4_BmAcro

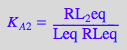
K_A_2 = RL_2eq/(Leq*RLeq)

First ligand-binding step:

eq2_2_4_Bmicro:
solve(%, RL_Ieq):
%[1][1]:
eq3_1_1_Bmicro:= RL_Ieq = %

eq2_2_5_Bmicro:
solve(%, RL_I_Ieq):
%[1][1]:
eq3_1_2_Bmicro:= RL_I_Ieq = %

Substitue into the mass balance for single-bound species

eq2_2_1_Bmicro:
% | eq3_1_1_Bmicro | eq3_1_2_Bmicro:
eq3_1_3_Bmicro:= %

Substitute into the expression for the mAcroscopic association constant

eq2_1_3_BmAcro:
% | eq3_1_3_Bmicro:
normal(%):
eq3_1_4_Bmicro:= %

=> this is a relationship between macroscopic association constant of the first step and microscopic constants of association for individual sites.

Second ligand-binding step:

eq2_2_6_Bmicro:
solve(%, RL_2eq):
%[1][1]:
eq3_1_5_Bmicro:= RL_2eq = %

Substitute into the expression for the mAcroscopic association constant

eq2_1_4_BmAcro:
% | eq2_2_1_Bmicro | eq3_1_5_Bmicro | eq3_1_1_Bmicro | eq3_1_2_Bmicro:
normal(%):
eq3_1_6_Bmicro:= %

=> This is the final expression

Remove the first-step constants (for convenience)

eq2_2_7_Bmicro:
solve(%, K_A_1_I):
%[1]:
eq3_1_7_Bmicro:= K_A_1_I =%

eq3_1_6_Bmicro | eq3_1_7_Bmicro:
normal(%):
eq3_1_8_Bmicro:= %

=> This is the final expression

Check against original literature:

assume that binding sites are identical and independent so that all individual association constants are identical to K. Now, express the equilibrium constants:

eq3_1_4_Bmicro;
% | K_A_1_I = K | K_A_1_I_I = K:
eq3_1_9_Bmicro:= %

and

eq3_1_8_Bmicro;
% | K_A_2_I = K | K_A_2_I_I = K :
eq3_1_10_Bmicro:= %

Mutual relationship of macroscopic constants in the first and the second association steps:

solve(eq3_1_10_Bmicro, K):
eq3_1_9_Bmicro | K = %[1]

Correct relationship! It is four times more difficult to saturate the second site than the have the first one bound due to multiplicity of the binding sites.

3.2 Microscopic B-bidentateL model (bi-dentate ligand)

Mass balance

eq2_3_1_Bbidentate

Macroscopic steps

eq2_1_3_BmAcro

K_A_1 = RLeq/(Leq*Req)

eq2_1_4_BmAcro

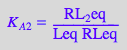
K_A_2 = RL_2eq/(Leq*RLeq)

First ligand-binding step

eq2_3_4_Bbidentate:
solve(%, RL_Ieq):
%[1][1]:
eq3_2_1_Bbidentate:= RL_Ieq = %

eq2_3_5_Bbidentate:
solve(%, RL_I_Ieq):
%[1][1]:
eq3_2_2_Bbidentate:= RL_I_Ieq = %

eq2_3_7_Bbidentate:
solve(%, RL_b_ieq):
%[1][1]:
eq3_2_3_Bbidentate:= RL_b_ieq = %

Substitute into mass balance

eq2_3_1_Bbidentate:
% | eq3_2_3_Bbidentate | eq3_2_2_Bbidentate | eq3_2_1_Bbidentate:
eq3_2_4_Bbidentate:= %

Substitute into the macroscopic equation of the first step

eq2_1_3_BmAcro:
% | eq3_2_4_Bbidentate:
normal(%):
eq3_2_5_Bbidentate:= %

=> final equation

Second ligand-binding step

eq2_3_6_Bbidentate:
solve(%, RL_2eq):
%[1][1]:
eq3_2_6_Bbidentate:= RL_2eq = %

Substitute into the macroscopic equation for the second step

eq2_1_4_BmAcro:
% | eq3_2_6_Bbidentate | eq3_2_4_Bbidentate | eq3_2_1_Bbidentate:
normal(%):
eq3_2_7_Bbidentate:= %

K_A_2 = (K_A_1_I*K_A_2_I_I)/(K_A_1_I + K_A_1_I_I + K_A_1_I*K_C_I_I)

=> final equation

Remove the first-step association constants (for convenience)

eq2_3_8_Bbidentate:
solve(%, K_A_1_I_I):
%[1]:
eq3_2_8_Bbidentate:= K_A_1_I_I = %

eq3_2_7_Bbidentate | eq3_2_8_Bbidentate:
normal(%):
eq3_2_9_Bbidentate:=%

K_A_2 = (K_A_2_I*K_A_2_I_I)/(K_A_2_I + K_A_2_I_I + K_A_2_I*K_C_I_I)

=> final equation

Evaluate the same test situation: set individual binding constants to identical values

eq3_2_5_Bbidentate:
% | K_A_1_I = K | K_A_1_I_I = K

eq3_2_7_Bbidentate:
% | K_A_1_I = K | K_A_1_I_I = K | K_A_2_I_I = K:
normal(%)

=> Result makes perfect sence. The greater K_C_II is the more single-bound species with open second site is removed from binding of the second ligand; the smaller the second macroscopic association constant looks like!

Summary of general relationships between microscopic and macroscopic binding constants

===== Microscopic B model (mono-dentate ligand) ======

Binding of the first ligand:

eq3_1_4_Bmicro

Binding of the second ligand:

eq3_1_8_Bmicro

Binding of the second ligand in independent constants:

eq3_1_6_Bmicro

===== Microscopic B-bidentateL model (bi-dentate ligand) ======

Binding of the first ligand:

eq3_2_5_Bbidentate

Binding of the second ligand:

eq3_2_9_Bbidentate

K_A_2 = (K_A_2_I*K_A_2_I_I)/(K_A_2_I + K_A_2_I_I + K_A_2_I*K_C_I_I)

Binding of the second ligand in independent constants:

eq3_2_7_Bbidentate

K_A_2 = (K_A_1_I*K_A_2_I_I)/(K_A_1_I + K_A_1_I_I + K_A_1_I*K_C_I_I)

Back to Contents

4. Derivation of equations for concentrations of species

I will prepare sets of equations separately for all three models.

4.1 Macroscopic B model

Goal: Express concentration of the free ligand, Leq, as a function of equilibrium constants and total concentrations.

Equations to use:

eq2_1_1_BmAcro

eq2_1_2_BmAcro

eq2_1_3_BmAcro

K_A_1 = RLeq/(Leq*Req)

eq2_1_4_BmAcro

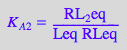
K_A_2 = RL_2eq/(Leq*RLeq)

STEP 1: Express all R-containing species starting from the higher stoichiometry

Express RL_2eq out of the equilibrium constant equation

eq2_1_4_BmAcro:
solve(%, RL_2eq):
%[1][1]:
eq4_1_1_BmAcro:= RL_2eq = %

Express RLeq out of the equilibrium constant equation

eq2_1_3_BmAcro:
solve(%, RLeq):
%[1][1]:
eq4_1_2_BmAcro:= RLeq = %

STEP 2: Substitute all into mass balance for L and express Req

eq2_1_2_BmAcro:
% | eq4_1_1_BmAcro | eq4_1_2_BmAcro:
eq4_1_3_BmAcro:= %

solve(eq4_1_3_BmAcro,Req):
%[1][1]:
eq4_1_4_BmAcro:= Req = %

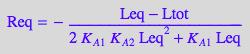
Req = -(Leq - Ltot)/(2*K_A_1*K_A_2*Leq^2 + K_A_1*Leq)

STEP 3: Substitute all into mass balance for R and attempt to solve for Leq

eq2_1_1_BmAcro :
% | eq4_1_1_BmAcro | eq4_1_2_BmAcro | eq4_1_4_BmAcro:
eq4_1_5_BmAcro:= %

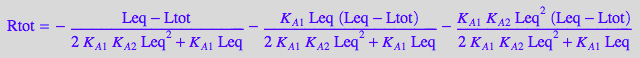
Rtot = - (Leq - Ltot)/(2*K_A_1*K_A_2*Leq^2 + K_A_1*Leq) - (K_A_1*Leq*(Leq - Ltot))/(2*K_A_1*K_A_2*Leq^2 + K_A_1*Leq) - (K_A_1*K_A_2*Leq^2*(Leq - Ltot))/(2*K_A_1*K_A_2*Leq^2 + K_A_1*Leq)

=> This is an expression for numerical solution

Try to solve analytically

solve(eq4_1_5_BmAcro, Leq)

=> analytically insoluble; use numeric solution

4.2 Microscopic B model (mono-dentate binding only

Goal: Express concentration of the free ligand, Leq, as a function of equilibrium constants and total concentrations.

Equations to use:

eq2_2_1_Bmicro

eq2_2_2_Bmicro

eq2_2_3_Bmicro

eq2_2_4_Bmicro

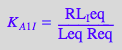
K_A_1_I = RL_Ieq/(Leq*Req)

eq2_2_5_Bmicro

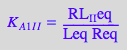
K_A_1_I_I = RL_I_Ieq/(Leq*Req)

eq2_2_6_Bmicro

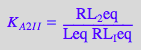
K_A_2_I_I = RL_2eq/(Leq*RL_Ieq)

STEP 1: Express all R-containing species starting from the higher stoichiometry

Express RL_2eq out of the equilibrium constant equation

eq2_2_6_Bmicro:
solve(%, RL_2eq):
%[1][1]:
eq4_2_1_Bmicro:= RL_2eq = %

Express RL_Ieq

eq2_2_4_Bmicro:
solve(%, RL_Ieq):
%[1][1]:
eq4_2_2_Bmicro:= RL_Ieq = %

Express RL_I_Ieq

eq2_2_5_Bmicro:
solve(%, RL_I_Ieq):
%[1][1]:
eq4_2_3_Bmicro:= RL_I_Ieq = %

STEP 2: Substitute all into mass balance for L and express Req

eq2_2_3_Bmicro:
% | eq4_2_1_Bmicro | eq2_2_1_Bmicro:
% | eq4_2_3_Bmicro | eq4_2_2_Bmicro:
solve(%, Req):
%[1][1]:
eq4_2_4_Bmicro:= Req = %

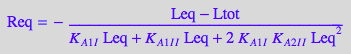
Req = -(Leq - Ltot)/(K_A_1_I*Leq + K_A_1_I_I*Leq + 2*K_A_1_I*K_A_2_I_I*Leq^2)

STEP 3: Substitute all into mass balance for R and attempt to solve for Leq

Rtot = - (Leq - Ltot)/(K_A_1_I*Leq + K_A_1_I_I*Leq + 2*K_A_1_I*K_A_2_I_I*Leq^2) - (K_A_1_I*Leq*(Leq - Ltot))/(K_A_1_I*Leq + K_A_1_I_I*Leq + 2*K_A_1_I*K_A_2_I_I*Leq^2) - (K_A_1_I_I*Leq*(Leq - Ltot))/(K_A_1_I*Leq + K_A_1_I_I*Leq + 2*K_A_1_I*K_A_2_I_I*Leq^2) - (K_A_1_I*K_A_2_I_I*Leq^2*(Leq - Ltot))/(K_A_1_I*Leq + K_A_1_I_I*Leq + 2*K_A_1_I*K_A_2_I_I*Leq^2)

=> final equation for numeric solution

try to solve

solve(eq4_2_5_Bmicro, Leq)

=> insoluble. Use the numeric solution

4.3 Microscopic B-bidentateL model (bi-dentate ligand binding)

Goal: Express concentration of the free ligand, Leq, as a function of equilibrium constants and total concentrations.

Equations to use:

eq2_3_1_Bbidentate

eq2_3_2_Bbidentate

eq2_3_3_Bbidentate

eq2_3_4_Bbidentate

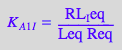
K_A_1_I = RL_Ieq/(Leq*Req)

eq2_3_5_Bbidentate

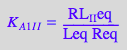
K_A_1_I_I = RL_I_Ieq/(Leq*Req)

eq2_3_6_Bbidentate

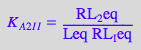
K_A_2_I_I = RL_2eq/(Leq*RL_Ieq)

eq2_3_7_Bbidentate

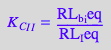
K_C_I_I = RL_b_ieq/RL_Ieq

STEP 1: Express all R-containing species starting from the higher stoichiometry

Express RL_2eq out of the equilibrium constant equation

eq2_3_6_Bbidentate:
solve(%, RL_2eq):
%[1][1]:
eq4_3_1_Bbidentate:= RL_2eq = %

Express RL_b_ieq

eq2_3_7_Bbidentate:
solve(%, RL_b_ieq):
%[1][1]:
eq4_3_2_Bbidentate:= RL_b_ieq = %

Express RL_Ieq

eq2_3_4_Bbidentate:
solve(%, RL_Ieq):
%[1][1]:
eq4_3_3_Bbidentate:= RL_Ieq = %

Express RL_I_Ieq

eq2_3_5_Bbidentate:
solve(%, RL_I_Ieq):
%[1][1]:
eq4_3_4_Bbidentate:= RL_I_Ieq = %

STEP 2: Substitute all into mass balance for L and express Req

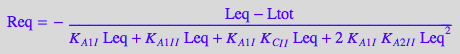
Req = -(Leq - Ltot)/(K_A_1_I*Leq + K_A_1_I_I*Leq + K_A_1_I*K_C_I_I*Leq + 2*K_A_1_I*K_A_2_I_I*Leq^2)

STEP 3: Substitute all into mass balance for R and attempt to solve for Leq

=> numeric solution

try to solve

S:=solve(eq4_3_6_Bbidentate, [Leq], Real)

matrix([[Leq]]) in Dom::Interval(0, Ltot) intersect RootOf(K_A_1_I*K_A_2_I_I*z^3 + 2*K_A_1_I*K_A_2_I_I*Rtot*z^2 - K_A_1_I*K_A_2_I_I*Ltot*z^2 + K_A_1_I*K_C_I_I*z^2 + K_A_1_I_I*z^2 + K_A_1_I*z^2 - K_A_1_I*K_C_I_I*Ltot*z + K_A_1_I*K_C_I_I*Rtot*z - K_A_1_I_I*Ltot*z - K_A_1_I*Ltot*z + K_A_1_I_I*Rtot*z + K_A_1_I*Rtot*z + z - Ltot, z)

=> insoluble

Summary of equations for equilibrium concentrations of species

NOTE: Rename all equations for easier use.

===== Macroscopic B model ========

Expression for numeric solution for Leq:

eqRtot_BmAcro:=eq4_1_5_BmAcro

Rtot = - (Leq - Ltot)/(2*K_A_1*K_A_2*Leq^2 + K_A_1*Leq) - (K_A_1*Leq*(Leq - Ltot))/(2*K_A_1*K_A_2*Leq^2 + K_A_1*Leq) - (K_A_1*K_A_2*Leq^2*(Leq - Ltot))/(2*K_A_1*K_A_2*Leq^2 + K_A_1*Leq)

Expressions for other species

eqReq_BmAcro:=eq4_1_4_BmAcro

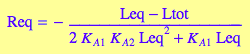
Req = -(Leq - Ltot)/(2*K_A_1*K_A_2*Leq^2 + K_A_1*Leq)

eqRLeq_BmAcro:=eq4_1_2_BmAcro

eqRL2eq_BmAcro:=eq4_1_1_BmAcro

====== Microscopic B model (mono-dentate binding only) =====

Expression for numeric solution for Leq:

eqRtot_Bmicro:=eq4_2_5_Bmicro

Expressions for other species

eqReq_Bmicro:=eq4_2_4_Bmicro

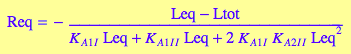
Req = -(Leq - Ltot)/(K_A_1_I*Leq + K_A_1_I_I*Leq + 2*K_A_1_I*K_A_2_I_I*Leq^2)

eqRLIIeq_Bmicro:=eq4_2_3_Bmicro

eqRLIeq_Bmicro:=eq4_2_2_Bmicro

eqRL2eq_Bmicro:=eq4_2_1_Bmicro

Expressions for dependent constants:

eqKA2I_Bmicro:=eq2_2_7_Bmicro

eqKB1_Bmicro:=eq2_2_8_Bmicro

===== Microscopic B-bidentateL model (bi-dentate ligand binding) =====

Expression for a numeric solution for Leq:

eqRtot_Bbidentate:=eq4_3_6_Bbidentate

Other species:

eqReq_Bbidentate:=eq4_3_5_Bbidentate

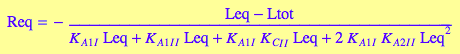
Req = -(Leq - Ltot)/(K_A_1_I*Leq + K_A_1_I_I*Leq + K_A_1_I*K_C_I_I*Leq + 2*K_A_1_I*K_A_2_I_I*Leq^2)

eqRLIIeq_Bbidentate:=eq4_3_4_Bbidentate

eqRLIeq_Bbidentate:=eq4_3_3_Bbidentate

eqRLbieq_Bbidentate:=eq4_3_2_Bbidentate

eqRL2eq_Bbidentate:=eq4_3_1_Bbidentate

Expressions for dependent constants:

eqKA2I_Bbidentate:=eq2_3_8_Bbidentate

eqKB1I_Bbidentate:=eq2_3_9_Bbidentate

eqKB2_Bbidentate:=eq2_3_10_Bbidentate

Back to Contents

5. Prepare equations for a numeric solution

Introduce a convenient variable LRratio=Ltot/Rtot

eqLRratio:= Ltot = LRratio * Rtot

5.1 Macroscopic B model

STEP 1: Make a function for numeric solving of Rtot equation

fRtot_BmAcro:= (Rtot, LRratio, Leq, K_A_1, K_A_2) --> eqRtot_BmAcro[2] | eqLRratio;

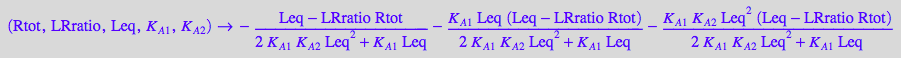
(Rtot, LRratio, Leq, K_A_1, K_A_2) -> - (Leq - LRratio*Rtot)/(2*K_A_1*K_A_2*Leq^2 + K_A_1*Leq) - (K_A_1*Leq*(Leq - LRratio*Rtot))/(2*K_A_1*K_A_2*Leq^2 + K_A_1*Leq) - (K_A_1*K_A_2*Leq^2*(Leq - LRratio*Rtot))/(2*K_A_1*K_A_2*Leq^2 + K_A_1*Leq)

Assume some constant values for testing

NOTE 1: Use different names for variables!!!

NOTE 2: Make sure the VALUES are all different and NOT just ORDER OF MAGNITUDS to make it easier for troubleshooting.

Rtot_value:=1e-3:
K_A_1_value:= 1e7:
K_A_2_value:= 1e8:
LR_ratio_max:= 2.5:
LR_ratio_value:= 0.8:
Leq_value:= 0.00000007373194321:

Test operation of the new function:

fRtot_BmAcro(Rtot_value, LR_ratio_value, Leq_value, K_A_1_value, K_A_2_value)

=> operational!

STEP 2: Define a procedure for numeric solving of this equation thus creating a function Leq=f(...)

/* WARNING: make sure the Leq search range starts with a non-zero number!!!!
* Use a number larger than that to create approximation of LRratio=0
*/

pnLeq_BmAcro:= proc(paramRtot, paramLRratio, paramK_A_1, paramK_A_2)

    /* NOTE: Parameter names should be different from
      variable names used in the equation!!!

      If you see an error message:
          "Error: Illegal operand [_index];
           during evaluation of 'your function name'"
      it means fsolve returned FAIL and you need to check
      values of all parameters passed to the function fRtot

    */

   local result;
   begin
      /* NOTE: Uncomment the strings below for debugging; comment out for normal operation.
       * Display what was entered: */

      //print(paramRtot, paramLRratio, paramK_A_1, paramK_A_2);

      /* Numerically solving the equation for Leq in a restricted range.
       * WARNING: make sure the range starts with a non-zero number!!!!
       */

      result:=numeric::fsolve(
            paramRtot - fRtot_BmAcro(paramRtot, paramLRratio, paramLeq, paramK_A_1, paramK_A_2),
            paramLeq=10e-32..paramRtot*paramLRratio);

     /* See the full result */
     //print(result);

     /* extract answer from equation */
     result[1][2]

end_proc;

Test operation:

pnLeq_BmAcro(Rtot_value, LR_ratio_value, K_A_1_value, K_A_2_value)

STEP 3: Define functions for equilibrium concentrations of all species

(begin with listing equations for the species)

Expressions for other species:

Req

eqReq_BmAcro;
pnReq_BmAcro:= proc(paramRtot, paramLRratio, paramK_A_1, paramK_A_2)
    local L;
    begin
      L:=pnLeq_BmAcro(paramRtot, paramLRratio, paramK_A_1, paramK_A_2);
      // Insert equation for this species and substitute all parameters
      eqReq_BmAcro[2] | Ltot=paramLRratio*paramRtot | Leq=L | K_A_1=paramK_A_1 | K_A_2=paramK_A_2;
    end_proc

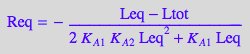
Req = -(Leq - Ltot)/(2*K_A_1*K_A_2*Leq^2 + K_A_1*Leq)

test

pnReq_BmAcro(Rtot_value, LR_ratio_value, K_A_1_value, K_A_2_value);

=>operational

RLeq

eqRLeq_BmAcro;
pnRLeq_BmAcro:= proc(paramRtot, paramLRratio, paramK_A_1, paramK_A_2)
    local L, R;
    begin
           L:=pnLeq_BmAcro(paramRtot, paramLRratio, paramK_A_1, paramK_A_2);
           R:=pnReq_BmAcro(paramRtot, paramLRratio, paramK_A_1, paramK_A_2);
      // Insert equation for this species and substitute all parameters
      eqRLeq_BmAcro[2] | Leq=L | Req=R | K_A_1=paramK_A_1 ;
    end_proc

Test

pnRLeq_BmAcro(Rtot_value, LR_ratio_value, K_A_1_value, K_A_2_value);

=> operational

eqRL2eq_BmAcro;
pnRL2eq_BmAcro:= proc(paramRtot, paramLRratio, paramK_A_1, paramK_A_2)
    local L, RL;
    begin
           L:=pnLeq_BmAcro(paramRtot, paramLRratio, paramK_A_1, paramK_A_2);
           RL:=pnRLeq_BmAcro(paramRtot, paramLRratio, paramK_A_1, paramK_A_2);
      // Insert equation for this species and substitute all parameters
      eqRL2eq_BmAcro[2] | Leq=L | RLeq=RL | K_A_2=paramK_A_2;
    end_proc

Test

pnRL2eq_BmAcro(Rtot_value, LR_ratio_value, K_A_1_value, K_A_2_value);

=> operational

STEP 4: Catch errors in substitution of equations (cut-and-paste glitches)

Collect all the test lines and re-run. Make sure all numbers come out different.

Cut-and-paste glitches come out as identical numbers.

pnLeq_BmAcro(Rtot_value, LR_ratio_value, K_A_1_value, K_A_2_value);
pnReq_BmAcro(Rtot_value, LR_ratio_value, K_A_1_value, K_A_2_value);
pnRLeq_BmAcro(Rtot_value, LR_ratio_value, K_A_1_value, K_A_2_value);
pnRL2eq_BmAcro(Rtot_value, LR_ratio_value, K_A_1_value, K_A_2_value);

=> All different! No cut-and-paste typos.

STEP 5: Collect all these names in Section 6 for saving on the disk.

5.2 Microscopic B model (mono-dentate binding only)

STEP 1: Make a function for numeric solving of Rtot equation

eqRtot_Bmicro:
fRtot_Bmicro:= (Rtot, LRratio, Leq, K_A_1_I, K_A_1_I_I, K_A_2_I_I) --> eqRtot_Bmicro[2] | eqLRratio;

Assume new constants

NOTE 1: Use different names for variables!!!

NOTE 2: Make sure the VALUES are all different and NOT just ORDER OF MAGNITUDS to make it easier for troubleshooting.

K_A_1_I_value:=1e4:
K_A_1_I_I_value:=1e6:
K_A_2_I_I_value:=1e5:
Leq_value:=0.0000001890503389: // taken from test of the procedure (below)

Test

fRtot_Bmicro(Rtot_value, LR_ratio_value, Leq_value, K_A_1_I_value, K_A_1_I_I_value, K_A_2_I_I_value)

=> operational

STEP 2: Define a procedure for numeric solving of this equation thus creating a function Leq=f(...)

/* WARNING: make sure the Leq search range starts with a non-zero number!!!!
* Use a number larger than that to create approximation of LRratio=0
*/

pnLeq_Bmicro:= proc(paramRtot, paramLRratio, paramK_A_1_I, paramK_A_1_I_I, paramK_A_2_I_I)

    /* NOTE: Parameter names should be different from
      variable names used in the equation!!!

      If you see an error message:
          "Error: Illegal operand [_index];
           during evaluation of 'your function name'"
      it means fsolve returned FAIL and you need to check
      values of all parameters passed to the function fRtot

    */

   local result;
   begin
      /* NOTE: Uncomment the strings below for debugging; comment out for normal operation.
       * Display what was entered: */

      //print(paramRtot, paramLRratio, paramK_A_1_I, paramK_A_1_I_I, paramK_A_2_I_I);

      /* Numerically solving the equation for Leq in a restricted range.
       * WARNING: make sure the range starts with a non-zero number!!!!
       */

      result:=numeric::fsolve(
            paramRtot - fRtot_Bmicro(paramRtot, paramLRratio, paramLeq, paramK_A_1_I, paramK_A_1_I_I, paramK_A_2_I_I),
            paramLeq=10e-32..paramRtot*paramLRratio);

     /* See the full result */
     //print(result);

     /* extract answer from equation */
     result[1][2]

end_proc;

test

pnLeq_Bmicro(Rtot_value, LR_ratio_value, K_A_1_I_value, K_A_1_I_I_value, K_A_2_I_I_value)

=> operational

STEP 3: Define functions for equilibrium concentrations of all species

(begin with listing equations for the species)

Expressions for other species:

Req

eqReq_Bmicro;
pnReq_Bmicro:= proc(paramRtot, paramLRratio, paramK_A_1_I, paramK_A_1_I_I, paramK_A_2_I_I)
    local L;
    begin
      L:=pnLeq_Bmicro(paramRtot, paramLRratio, paramK_A_1_I, paramK_A_1_I_I, paramK_A_2_I_I);
      // Insert equation for this species and substitute all parameters
      eqReq_Bmicro[2] | Ltot=paramLRratio*paramRtot | Leq=L | K_A_1_I=paramK_A_1_I | K_A_1_I_I=paramK_A_1_I_I | K_A_2_I_I=paramK_A_2_I_I ;
    end_proc

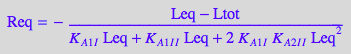
Req = -(Leq - Ltot)/(K_A_1_I*Leq + K_A_1_I_I*Leq + 2*K_A_1_I*K_A_2_I_I*Leq^2)

test

pnReq_Bmicro(Rtot_value, LR_ratio_value, K_A_1_I_value, K_A_1_I_I_value, K_A_2_I_I_value)

RLIIeq

eqRLIIeq_Bmicro;
pnRLIIeq_Bmicro:= proc(paramRtot, paramLRratio, paramK_A_1_I, paramK_A_1_I_I, paramK_A_2_I_I)
    local L, R;
    begin
      L:=pnLeq_Bmicro(paramRtot, paramLRratio, paramK_A_1_I, paramK_A_1_I_I, paramK_A_2_I_I);
      R:=pnReq_Bmicro(paramRtot, paramLRratio, paramK_A_1_I, paramK_A_1_I_I, paramK_A_2_I_I);
      // Insert equation for this species and substitute all parameters
      eqRLIIeq_Bmicro[2] | Ltot=paramLRratio*paramRtot | Leq=L | Req=R | K_A_1_I=paramK_A_1_I | K_A_1_I_I=paramK_A_1_I_I | K_A_2_I_I=paramK_A_2_I_I ;
    end_proc

test

pnRLIIeq_Bmicro(Rtot_value, LR_ratio_value, K_A_1_I_value, K_A_1_I_I_value, K_A_2_I_I_value)

=> operational

RLIeq

eqRLIeq_Bmicro;
pnRLIeq_Bmicro:= proc(paramRtot, paramLRratio, paramK_A_1_I, paramK_A_1_I_I, paramK_A_2_I_I)
    local L, R;
    begin
      L:=pnLeq_Bmicro(paramRtot, paramLRratio, paramK_A_1_I, paramK_A_1_I_I, paramK_A_2_I_I);
      R:=pnReq_Bmicro(paramRtot, paramLRratio, paramK_A_1_I, paramK_A_1_I_I, paramK_A_2_I_I);
      // Insert equation for this species and substitute all parameters
      eqRLIeq_Bmicro[2] | Ltot=paramLRratio*paramRtot | Leq=L | Req=R | K_A_1_I=paramK_A_1_I | K_A_1_I_I=paramK_A_1_I_I | K_A_2_I_I=paramK_A_2_I_I ;
    end_proc

test

pnRLIeq_Bmicro(Rtot_value, LR_ratio_value, K_A_1_I_value, K_A_1_I_I_value, K_A_2_I_I_value)

RL2eq

eqRL2eq_Bmicro;
pnRL2eq_Bmicro:= proc(paramRtot, paramLRratio, paramK_A_1_I, paramK_A_1_I_I, paramK_A_2_I_I)
    local L, RLI;
    begin
      L:=pnLeq_Bmicro(paramRtot, paramLRratio, paramK_A_1_I, paramK_A_1_I_I, paramK_A_2_I_I);
      RLI:=pnRLIeq_Bmicro(paramRtot, paramLRratio, paramK_A_1_I, paramK_A_1_I_I, paramK_A_2_I_I);
      // Insert equation for this species and substitute all parameters
      eqRL2eq_Bmicro[2] | Ltot=paramLRratio*paramRtot | Leq=L | RL_Ieq=RLI | K_A_1_I=paramK_A_1_I | K_A_1_I_I=paramK_A_1_I_I | K_A_2_I_I=paramK_A_2_I_I ;
    end_proc

test

pnRL2eq_Bmicro(Rtot_value, LR_ratio_value, K_A_1_I_value, K_A_1_I_I_value, K_A_2_I_I_value)

=> operational

STEP 4: Catch errors in substitution of equations (cut-and-paste glitches)

Collect all the test lines and re-run. Make sure all numbers come out different.

Cut-and-paste glitches come out as identical numbers.

pnLeq_Bmicro(Rtot_value, LR_ratio_value, K_A_1_I_value, K_A_1_I_I_value, K_A_2_I_I_value);
pnReq_Bmicro(Rtot_value, LR_ratio_value, K_A_1_I_value, K_A_1_I_I_value, K_A_2_I_I_value);
pnRLIIeq_Bmicro(Rtot_value, LR_ratio_value, K_A_1_I_value, K_A_1_I_I_value, K_A_2_I_I_value);
pnRLIeq_Bmicro(Rtot_value, LR_ratio_value, K_A_1_I_value, K_A_1_I_I_value, K_A_2_I_I_value);
pnRL2eq_Bmicro(Rtot_value, LR_ratio_value, K_A_1_I_value, K_A_1_I_I_value, K_A_2_I_I_value);

=> all different! Good. No cut-and-paste typos.

STEP 5: Collect all these names in Section 6 for saving on the disk.

5.3 Microscopic B-bidentatateL model (bi-dentate ligand)

STEP 1: Make a function for numeric solving of Rtot equation

fRtot_Bbidentate:= (Rtot, LRratio, Leq, K_A_1_I, K_A_1_I_I, K_A_2_I_I, K_C_I_I) --> eqRtot_Bbidentate[2] | eqLRratio;

Assume new constants

NOTE 1: Use different names for variables!!!

NOTE 2: Make sure the VALUES are all different and NOT just ORDER OF MAGNITUDS to make it easier for troubleshooting.

Rtot_value:=1e-3:
LR_ratio_value:= 0.5:
K_A_1_I_value:=2e4:
K_A_1_I_I_value:=1e2:
K_A_2_I_I_value:=3e5:
K_C_I_I_value:=11:

test

fRtot_Bbidentate(Rtot_value, LR_ratio_value, Leq_value, K_A_1_I_value, K_A_1_I_I_value, K_A_2_I_I_value, K_C_I_I_value)

=> operational

STEP 2: Define a procedure for numeric solving of this equation thus creating a function Leq=f(...)

/* WARNING: make sure the Leq search range starts with a non-zero number!!!!
* Use a number larger than that to create approximation of LRratio=0
*/

pnLeq_Bbidentate:= proc(paramRtot, paramLRratio, paramK_A_1_I, paramK_A_1_I_I, paramK_A_2_I_I, paramK_C_I_I)

    /* NOTE: Parameter names should be different from
      variable names used in the equation!!!

      If you see an error message:
          "Error: Illegal operand [_index];
           during evaluation of 'your function name'"
      it means fsolve returned FAIL and you need to check
      values of all parameters passed to the function fRtot

    */

   local result;
   begin
      /* NOTE: Uncomment the strings below for debugging; comment out for normal operation.
       * Display what was entered: */

      //print(paramRtot, paramLRratio, paramK_A_1_I, paramK_A_1_I_I, paramK_A_2_I_I, paramK_C_I_I);

      /* Numerically solving the equation for Leq in a restricted range.
       * WARNING: make sure the range starts with a non-zero number!!!!
       */

      result:=numeric::fsolve(
            paramRtot - fRtot_Bbidentate(paramRtot, paramLRratio, paramLeq, paramK_A_1_I, paramK_A_1_I_I, paramK_A_2_I_I, paramK_C_I_I),
            paramLeq=10e-32..paramRtot*paramLRratio);

     /* See the full result */
     //print(result);

     /* extract answer from equation */
     result[1][2]

end_proc;

test

pnLeq_Bbidentate(Rtot_value, LR_ratio_value, K_A_1_I_value, K_A_1_I_I_value, K_A_2_I_I_value, K_C_I_I_value)

STEP 3: Define functions for equilibrium concentrations of all species

(begin with listing equations for the species)

Expressions for other species:

Req

eqReq_Bbidentate;
pnReq_Bbidentate:= proc(paramRtot, paramLRratio, paramK_A_1_I, paramK_A_1_I_I, paramK_A_2_I_I, paramK_C_I_I)
    local L;
    begin
      L:=pnLeq_Bbidentate(paramRtot, paramLRratio, paramK_A_1_I, paramK_A_1_I_I, paramK_A_2_I_I, paramK_C_I_I);
      // Insert equation for this species and substitute all parameters
      eqReq_Bbidentate[2] | Ltot=paramLRratio*paramRtot | Leq=L | K_A_1_I=paramK_A_1_I | K_A_1_I_I=paramK_A_1_I_I | K_A_2_I_I=paramK_A_2_I_I | K_C_I_I=paramK_C_I_I;
    end_proc

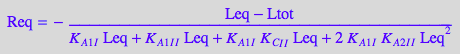
Req = -(Leq - Ltot)/(K_A_1_I*Leq + K_A_1_I_I*Leq + K_A_1_I*K_C_I_I*Leq + 2*K_A_1_I*K_A_2_I_I*Leq^2)

test

pnReq_Bbidentate(Rtot_value, LR_ratio_value, K_A_1_I_value, K_A_1_I_I_value, K_A_2_I_I_value, K_C_I_I_value)

RLIeq

eqRLIeq_Bbidentate;
pnRLIeq_Bbidentate:= proc(paramRtot, paramLRratio, paramK_A_1_I, paramK_A_1_I_I, paramK_A_2_I_I, paramK_C_I_I)
    local L, R;
    begin
      L:=pnLeq_Bbidentate(paramRtot, paramLRratio, paramK_A_1_I, paramK_A_1_I_I, paramK_A_2_I_I, paramK_C_I_I);
      R:=pnReq_Bbidentate(paramRtot, paramLRratio, paramK_A_1_I, paramK_A_1_I_I, paramK_A_2_I_I, paramK_C_I_I);
      // Insert equation for this species and substitute all parameters
      eqRLIeq_Bbidentate[2] | Ltot=paramLRratio*paramRtot | Leq=L | Req=R | K_A_1_I=paramK_A_1_I | K_A_1_I_I=paramK_A_1_I_I | K_A_2_I_I=paramK_A_2_I_I | K_C_I_I=paramK_C_I_I;
    end_proc

test

pnRLIeq_Bbidentate(Rtot_value, LR_ratio_value, K_A_1_I_value, K_A_1_I_I_value, K_A_2_I_I_value, K_C_I_I_value)

RLIIeq

eqRLIIeq_Bbidentate;
pnRLIIeq_Bbidentate:= proc(paramRtot, paramLRratio, paramK_A_1_I, paramK_A_1_I_I, paramK_A_2_I_I, paramK_C_I_I)
    local L, R;
    begin
      L:=pnLeq_Bbidentate(paramRtot, paramLRratio, paramK_A_1_I, paramK_A_1_I_I, paramK_A_2_I_I, paramK_C_I_I);
      R:=pnReq_Bbidentate(paramRtot, paramLRratio, paramK_A_1_I, paramK_A_1_I_I, paramK_A_2_I_I, paramK_C_I_I);
      // Insert equation for this species and substitute all parameters
      eqRLIIeq_Bbidentate[2] | Ltot=paramLRratio*paramRtot | Leq=L | Req=R | K_A_1_I=paramK_A_1_I | K_A_1_I_I=paramK_A_1_I_I | K_A_2_I_I=paramK_A_2_I_I | K_C_I_I=paramK_C_I_I;
    end_proc

test

pnRLIIeq_Bbidentate(Rtot_value, LR_ratio_value, K_A_1_I_value, K_A_1_I_I_value, K_A_2_I_I_value, K_C_I_I_value)

RLbieq

eqRLbieq_Bbidentate;
pnRLbieq_Bbidentate:= proc(paramRtot, paramLRratio, paramK_A_1_I, paramK_A_1_I_I, paramK_A_2_I_I, paramK_C_I_I)
    local L, RLI;
    begin
      L:=pnLeq_Bbidentate(paramRtot, paramLRratio, paramK_A_1_I, paramK_A_1_I_I, paramK_A_2_I_I, paramK_C_I_I);
      RLI:=pnRLIeq_Bbidentate(paramRtot, paramLRratio, paramK_A_1_I, paramK_A_1_I_I, paramK_A_2_I_I, paramK_C_I_I);
      // Insert equation for this species and substitute all parameters
      eqRLbieq_Bbidentate[2] | Ltot=paramLRratio*paramRtot | Leq=L | RL_Ieq=RLI | K_A_1_I=paramK_A_1_I | K_A_1_I_I=paramK_A_1_I_I | K_A_2_I_I=paramK_A_2_I_I | K_C_I_I=paramK_C_I_I;
    end_proc

test

pnRLbieq_Bbidentate(Rtot_value, LR_ratio_value, K_A_1_I_value, K_A_1_I_I_value, K_A_2_I_I_value, K_C_I_I_value)

RL2eq

eqRL2eq_Bbidentate;
pnRL2eq_Bbidentate:= proc(paramRtot, paramLRratio, paramK_A_1_I, paramK_A_1_I_I, paramK_A_2_I_I, paramK_C_I_I)
    local L, RLI;
    begin
      L:=pnLeq_Bbidentate(paramRtot, paramLRratio, paramK_A_1_I, paramK_A_1_I_I, paramK_A_2_I_I, paramK_C_I_I);
      RLI:=pnRLIeq_Bbidentate(paramRtot, paramLRratio, paramK_A_1_I, paramK_A_1_I_I, paramK_A_2_I_I, paramK_C_I_I);
      // Insert equation for this species and substitute all parameters
      eqRL2eq_Bbidentate[2] | Ltot=paramLRratio*paramRtot | Leq=L | RL_Ieq=RLI | K_A_1_I=paramK_A_1_I | K_A_1_I_I=paramK_A_1_I_I | K_A_2_I_I=paramK_A_2_I_I | K_C_I_I=paramK_C_I_I;
    end_proc

test

pnRL2eq_Bbidentate(Rtot_value, LR_ratio_value, K_A_1_I_value, K_A_1_I_I_value, K_A_2_I_I_value, K_C_I_I_value)

STEP 4: Catch errors in substitution of equations (cut-and-paste glitches)

Collect all the test lines and re-run. Make sure all numbers come out different.

Cut-and-paste glitches come out as identical numbers.

pnLeq_Bbidentate(Rtot_value, LR_ratio_value, K_A_1_I_value, K_A_1_I_I_value, K_A_2_I_I_value, K_C_I_I_value);
pnReq_Bbidentate(Rtot_value, LR_ratio_value, K_A_1_I_value, K_A_1_I_I_value, K_A_2_I_I_value, K_C_I_I_value);
pnRLIeq_Bbidentate(Rtot_value, LR_ratio_value, K_A_1_I_value, K_A_1_I_I_value, K_A_2_I_I_value, K_C_I_I_value);
pnRLIIeq_Bbidentate(Rtot_value, LR_ratio_value, K_A_1_I_value, K_A_1_I_I_value, K_A_2_I_I_value, K_C_I_I_value);
pnRLbieq_Bbidentate(Rtot_value, LR_ratio_value, K_A_1_I_value, K_A_1_I_I_value, K_A_2_I_I_value, K_C_I_I_value);
pnRL2eq_Bbidentate(Rtot_value, LR_ratio_value, K_A_1_I_value, K_A_1_I_I_value, K_A_2_I_I_value, K_C_I_I_value);

=> all different. OK

STEP 5: Collect all these names in Section 6 for saving on the disk.

Back to Contents

6. Save results on disk for future use

(you can retrieve them later by executing: fread(filename,Quiet))

ProjectName;
CurrentPath

Save all numeric solutions:

filename:=CurrentPath.ProjectName.".mb";
write(filename,

// Macroscopic B model
// - equations
eqRtot_BmAcro,
eqReq_BmAcro,
eqRLeq_BmAcro,
eqRL2eq_BmAcro,
// - procedures
fRtot_BmAcro,
pnLeq_BmAcro,
pnReq_BmAcro,
pnRLeq_BmAcro,
pnRL2eq_BmAcro,

// Microscopic B model (mono-dentate binding only)
// - equations
eqRtot_Bmicro,
eqReq_Bmicro,
eqRLIIeq_Bmicro,
eqRLIeq_Bmicro,
eqRL2eq_Bmicro,
// - dependent constants
eqKA2I_Bmicro,
eqKB1_Bmicro,
// - procedures
fRtot_Bmicro,
pnLeq_Bmicro,
pnReq_Bmicro,
pnRLIIeq_Bmicro,
pnRLIeq_Bmicro,
pnRL2eq_Bmicro,

// Microscopic B-bidentateL model (bi-dentate ligand)
// - equations
eqRtot_Bbidentate,
eqReq_Bbidentate,
eqRLIIeq_Bbidentate,
eqRLIeq_Bbidentate,
eqRLbieq_Bbidentate,
eqRL2eq_Bbidentate,

// - dependent contants
eqKA2I_Bbidentate,
eqKB1I_Bbidentate,
eqKB2_Bbidentate,

// - procedures
fRtot_Bbidentate,
pnLeq_Bbidentate,
pnReq_Bbidentate,
pnRLIeq_Bbidentate,
pnRLIIeq_Bbidentate,
pnRLbieq_Bbidentate,
pnRL2eq_Bbidentate

)

"/Volumes/Leopard_Partition/Users/kovrigin/Documents/Workspace/Global Analysis/IDAP/Mathematical_models/Equilibrium_thermodynamic_models/B_family_models/B_family_models_derivation.mb"

Conclusions

Derivation of all three models have been completed. All three checked out correctly in the next (analysis) step. Ready for implementation in IDAP.

Back to Contents