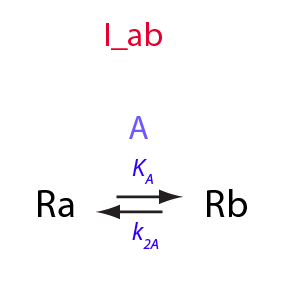
Derivation of equations for I_ab model

 

Simple intramolecular isomerization

 

image

 

 

 

 

Contents

 

Goals

 

1. Definitions

 

2. Derivation of a main equation

 

 

3. Define functions for equilibrium concentrations

 

4. Test if solution is meaningful

 

5. Check whether the solution satisfies all initial equation and conditions

 

6. Save results on disk for future use

 

 

Conclusions

 

 

 

Back to Contents

 

 

 

 

Goals

 

In this notebook I will formally derive equations for the simplest isomerization equilibrium

 

Analysis will be done in I_ab_analysis.mn

 

 

 

 

Back to Contents

 

 

 

 

 

1. Definitions

 

clean up workspace

reset()

 

Set path to save results into:

ProjectName:="I_ab";
CurrentPath:="/Users/kovrigin/Documents/Workspace/Global Analysis/IDAP/Mathematical_models/Equilibrium_thermodynamic_models/I_ab/";

"I_ab"
"/Users/kovrigin/Documents/Workspace/Global Analysis/IDAP/Mathematical_models/Equilibrium_thermodynamic_models/I_ab/"

 

 

 

 

 

 

 

Isomerization constant

 

These relationships serve as restraints for solve(), but not restrict these values in calculations!

 

K_A

K_A ;
assume(K_A  > 0):
assumeAlso(K_A , R_):

K_A

 

 

 

Total concentrations

 

Rtot - total concentration of the molecule

Rtot;
assumeAlso(Rtot>0):
assumeAlso(Rtot,R_):

Rtot

 

 

Common equilibrium concentrations

 

Raeq - equilibrium concentration of Ra form

Raeq;
assumeAlso(Raeq>0):
assumeAlso(Raeq<Rtot):
assumeAlso(Raeq,R_):

Raeq

Rbeq - equilibrium concentration of Rb form

Rbeq;
assumeAlso(Rbeq>0):
assumeAlso(Rbeq<Rtot):
assumeAlso(Rbeq,R_):

Rbeq

 

 

 

 

anames(Properties,User);

{K_A, Raeq, Rbeq, Rtot}

 

 

 

Back to Contents

 

 

 

 

2. Derivation of a main equation

 

 

 

Total concentrations of the molecule

eq2_1:= Rtot = Raeq + Rbeq

Rtot = Raeq + Rbeq

 

 

Write equilibrium thermodynamics equations

eq2_2:= K_A = Rbeq / Raeq

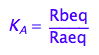
K_A = Rbeq/Raeq

 

 

Express Raeq as a function of all constants and total concentrations

 

Express Rbeq

eq2_2;
solve(%,Rbeq);
%[1][1];
eq2_3:= Rbeq= %

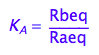
K_A = Rbeq/Raeq
piecewise([K_A*Raeq in Dom::Interval(0, Rtot), {K_A*Raeq}], [not K_A*Raeq in Dom::Interval(0, Rtot), {}])
K_A*Raeq
Rbeq = K_A*Raeq

 

 

Substitute to the mass balance equation

eq2_1;
% | eq2_3;
eq2_4:= %:

Rtot = Raeq + Rbeq
Rtot = Raeq + K_A*Raeq

 

Express Raeq

eq2_4;
solve(%, Raeq);
eq2_5:= Raeq=%[1]

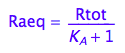
Rtot = Raeq + K_A*Raeq
{Rtot/(K_A + 1)}
Raeq = Rtot/(K_A + 1)

 

Express Rbeq

eq2_3;
eq2_6:= % | eq2_5;

Rbeq = K_A*Raeq
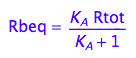
Rbeq = (K_A*Rtot)/(K_A + 1)

 

 

 

 

Summary  of equations for all species

 

Independent parameters:

Rtot, K_A

Rtot, K_A

 

 

 

[Ra]

eq2_5

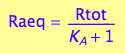
Raeq = Rtot/(K_A + 1)

[Rb]

eq2_6

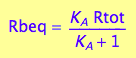
Rbeq = (K_A*Rtot)/(K_A + 1)

 

 

 

 

 

 

 

 

 

Generate functions

fRaeq:= (Rtot, K_A) --> eq2_5[2]

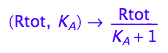
(Rtot, K_A) -> Rtot/(K_A + 1)

fRbeq:= (Rtot, K_A) --> eq2_6[2]

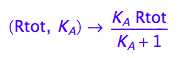
(Rtot, K_A) -> (K_A*Rtot)/(K_A + 1)

 

 

 

 

Back to Contents

 

 

 

4. Test if solution is meaningful

 

Set some realistic values for constants:

Total_R:=1;
Ka:=0.5;

1
0.5

Test that all equilibrium concentrations are positive values:

fRaeq(Total_R, Ka);
fRbeq(Total_R, Ka);
if (fRaeq(Total_R, Ka)>0 and
    fRbeq(Total_R, Ka)>0
        )

  then
   print(Unquoted,"Solution is meaningful.");
  else
   print(Unquoted,"WARNING!!!!");
   print(Unquoted,"Solution is NOT meaningful: some concentrations become negative!");
end_if

0.6666666667
0.3333333333
Solution is meaningful.

 

 

 

 

Back to Contents

 

 

 

5. Check whether the solution satisfies all initial equation and conditions

 

 

Here are all original independent

equations:

eq2_1;eq2_2;

Rtot = Raeq + Rbeq
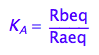
K_A = Rbeq/Raeq

 

Test eq2_1

eq2_1;
% | eq2_5 | eq2_6;
normal(%);
bool(%)

Rtot = Raeq + Rbeq
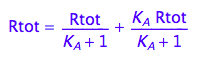
Rtot = Rtot/(K_A + 1) + (K_A*Rtot)/(K_A + 1)
Rtot = Rtot
TRUE

 

 

The found solution satisfies all original equations

 

 

 

 

 

Back to Contents

 

 

 

 

5. Save results on disk for future use

(you can retrieve them later by executing: fread(filename,Quiet))

 

 

 

 

ProjectName

"I_ab"

 

Eq_Raeq_I_ab:= eq2_5;
Eq_Rbeq_I_ab:= eq2_6;

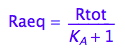
Raeq = Rtot/(K_A + 1)
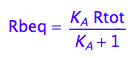
Rbeq = (K_A*Rtot)/(K_A + 1)

 

 

Reassign function names

fRaeq_I_ab:=fRaeq:
fRbeq_I_ab:=fRbeq:

 

filename:=CurrentPath.ProjectName.".mb";
write(filename,Eq_Raeq_I_ab,Eq_Rbeq_I_ab, fRaeq_I_ab, fRbeq_I_ab)

"/Users/kovrigin/Documents/Workspace/Global Analysis/IDAP/Mathematical_models/Equilibrium_thermodynamic_models/I_ab/I_ab.mb"

 

 

Conclusions

 

1. I derived analytical solutions for the I_ab system

 

 

 

Back to Contents