Testing the I_ab model

The I_ab_T model is the simplest two-state isomerization model with the temperature dependence

Contents

close all
clear all

Here you will find all figures

figures_folder='I_ab_T_testing_figures';

Test Computation of Equilibrium Concentrations

Set some meaningful parameters

R_gas=8.314510; % Gas constant J /mol /K
Rtotal=1; % Receptor concentration, M

% these are the constants we want to create
K_array=[0.25 0.5  1 2  4 ];

dH= 20000;  % J/mol
dS= 80; % J/mol/K

T_array=[];
for counter=1:length(K_array)
    % compute temperature
    T= dH./(dS-R_gas*log(K_array(counter)));
    T_array = [T_array ; T];
end
figure_handle=equilibrium_thermodynamic_equations.plot_populations(...
    T_array, K_array, {'K'}, 'K vs. T', ...
    [min(T_array) max(T_array) ], [0 max(K_array) ]);
xlabel('Temperature, K','FontSize',14);
ylabel('Equilibrium constant','FontSize',14);
% save it
results_output.output_figure(figure_handle, figures_folder, 'K_plot');

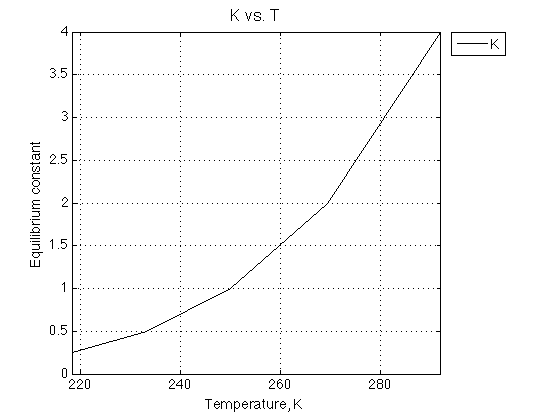
Set appropriate options for the model (see model file for details)

model_numeric_solver='analytical'  ;
model_numeric_options='n/a';

concentrations_array=[];
for counter=1:length(T_array)
    % compute
    [concentrations species_names] = equilibrium_thermodynamic_equations.I_ab_T_model(...
        Rtotal, T_array(counter), dH, dS,...
        model_numeric_solver, model_numeric_options);
    % collect
    concentrations_array = [concentrations_array ; concentrations];
end

Plot

Figure_title= 'I_ab_T model';
X_range=[min(T_array) max(T_array)+0.1 ]; % extend X just a bit past last point
Y_range=[0 Rtotal ]; % keep automatic scaling for Y
% display figure
figure_handle=equilibrium_thermodynamic_equations.plot_populations(...
    T_array, concentrations_array, species_names, Figure_title, X_range, Y_range);
xlabel('Temperature, K','FontSize',14);
% save it
results_output.output_figure(figure_handle, figures_folder, 'Concentrations_plot');

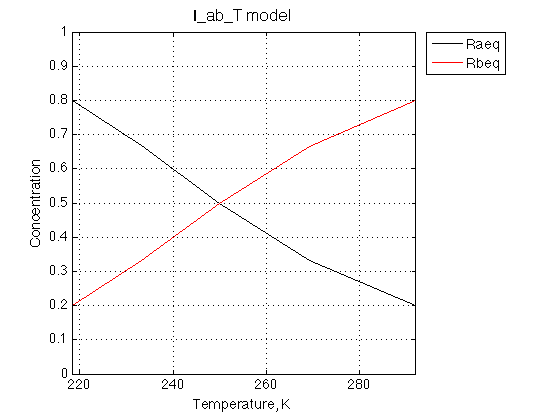
Observations

The ratio between Ra and Rb forms changes appropriately with K_A value.

Conclusion

The model equilibrium_thermodynamic_equations.I_ab_model() works well.

Published with MATLAB® 7.13