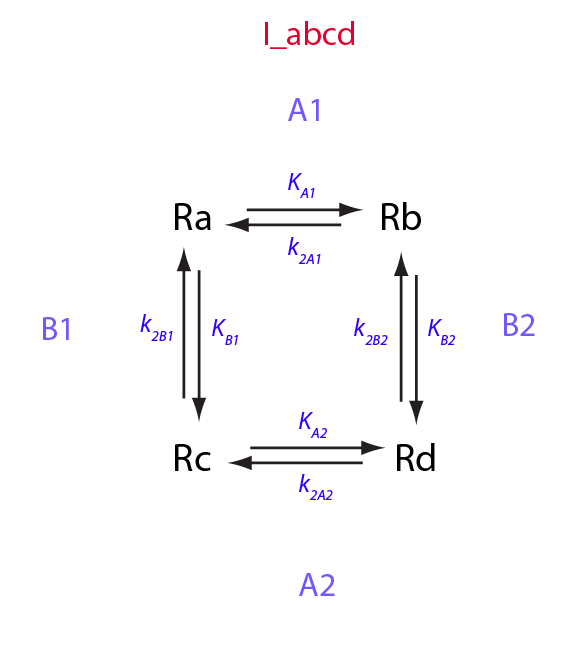
Analysis of I_abcd model

 

 

Intramolecular isomerization between four forms

 

image

 

 

 

 

Contents

 

Goals

 

1. Load equations

 

2. 2D plotting

 

3. ITC curve simulation

 

4. Summary of some graphical results

 

5. Testing numeric solutions

 

6. Reproduce a graph for equilibrium concentrations using a numeric solution

 

7. Save results on disk for future use

 

 

Conclusions

 

 

 

Back to Contents

 

Goals

 

In this notebook I will analyze and test the I_abcd model.

 

 

Back to Contents

 

 

 

1. Load equations

 

clean up workspace

reset()

 

 

 

Set path to save results into:

ProjectName:="I_abcd";
CurrentPath:="/Users/kovrigin/Documents/Workspace/Global Analysis/IDAP/Mathematical_models/Equilibrium_thermodynamic_models/I_abcd/";

"I_abcd"
"/Users/kovrigin/Documents/Workspace/Global Analysis/IDAP/Mathematical_models/Equilibrium_thermodynamic_models/I_abcd/"

 

 

 

 

 

Read results of derivations

filename:=CurrentPath.ProjectName.".mb";
fread(filename,Quiet):

"/Users/kovrigin/Documents/Workspace/Global Analysis/IDAP/Mathematical_models/Equilibrium_thermodynamic_models/I_abcd/I_abcd.mb"

 

 

Display equations (change : for ; to see the equation. Makes Mupad slow if all shown)

Eq_Raeq_I_abcd;
Eq_Rbeq_I_abcd;
Eq_Rceq_I_abcd;
Eq_Rdeq_I_abcd;
Eq_KB2_I_abcd;

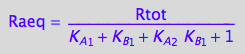
Raeq = Rtot/(K_A_1 + K_B_1 + K_A_2*K_B_1 + 1)
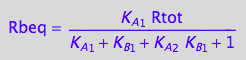
Rbeq = (K_A_1*Rtot)/(K_A_1 + K_B_1 + K_A_2*K_B_1 + 1)
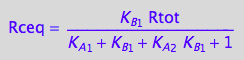
Rceq = (K_B_1*Rtot)/(K_A_1 + K_B_1 + K_A_2*K_B_1 + 1)
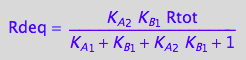
Rdeq = (K_A_2*K_B_1*Rtot)/(K_A_1 + K_B_1 + K_A_2*K_B_1 + 1)
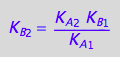
K_B_2 = (K_A_2*K_B_1)/K_A_1

 

 

Display functions

fRaeq_I_abcd;
fRbeq_I_abcd;
fRceq_I_abcd;
fRdeq_I_abcd

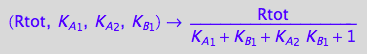
(Rtot, K_A_1, K_A_2, K_B_1) -> Rtot/(K_A_1 + K_B_1 + K_A_2*K_B_1 + 1)
(Rtot, K_A_1, K_A_2, K_B_1) -> (K_A_1*Rtot)/(K_A_1 + K_B_1 + K_A_2*K_B_1 + 1)
(Rtot, K_A_1, K_A_2, K_B_1) -> (K_B_1*Rtot)/(K_A_1 + K_B_1 + K_A_2*K_B_1 + 1)
(Rtot, K_A_1, K_A_2, K_B_1) -> (K_A_2*K_B_1*Rtot)/(K_A_1 + K_B_1 + K_A_2*K_B_1 + 1)

 

 

 

 

Back to Contents

 

 

 

2. 2D plotting

 

 

 

 

 

Set some realistic values for constants:

Total_R:=1;
Ka1:=5;
Ka2:=5;
Kb1:=2;
K_max:=10;

1
5
5
2
10

 

 

 

pRaeq:=  plot::Function2d(
          Function=(fRaeq_I_abcd(Total_R, K_A_1, Ka2, Kb1)),
          LegendText="[Ra]",
          Color = RGB::Black,
          XMin=(0),
          XMax=(K_max),
          XName=(K_A_1),
          TitlePositionX=(0)):

pRbeq:=  plot::Function2d(
          Function=(fRbeq_I_abcd(Total_R, K_A_1, Ka2, Kb1)),
          LegendText="[Rb]",
          Color = RGB::Blue,
          XMin=(0),
          XMax=(K_max),
          XName=(K_A_1),
          TitlePositionX=(0)):

pRceq:=  plot::Function2d(
          Function=(fRceq_I_abcd(Total_R, K_A_1, Ka2, Kb1)),
          LegendText="[Rc]",
          Color = RGB::Green,
          XMin=(0),
          XMax=(K_max),
          XName=(K_A_1),
          TitlePositionX=(0)):



pRdeq:=  plot::Function2d(
          Function=(fRdeq_I_abcd(Total_R, K_A_1, Ka2, Kb1)),
          LegendText="[Rd]",
          Color = RGB::Red,
          XMin=(0),
          XMax=(K_max),
          XName=(K_A_1),
          TitlePositionX=(0)):

plot(pRaeq,pRbeq,pRceq,pRdeq, YAxisTitle="M",
   Height=180, Width=160,TicksLabelFont=["Helvetica",12,[0,0,0],Left],
  AxesTitleFont=["Helvetica",14,[0,0,0],Left],
  XGridVisible=TRUE, YGridVisible=TRUE,
  LegendVisible=TRUE, LegendFont=["Helvetica",14,[0,0,0],Left],
  ViewingBoxYMin=0, ViewingBoxYMax=1);



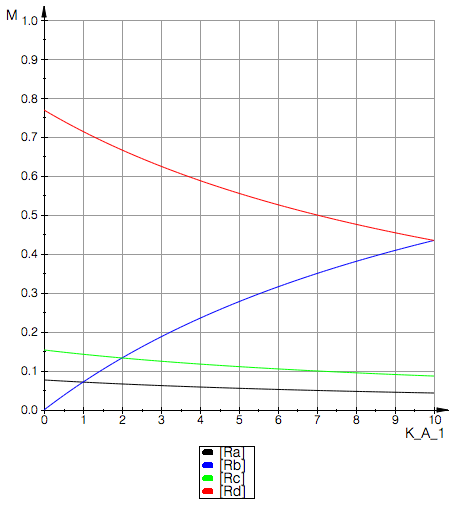
MuPAD graphics

 

 

 

 

Back to Contents

 

 

 

4. Summary of some results

 

Simple test results

 

Total_R:=1;
Ka1:=variable
Ka2:=5;
Kb1:=0;
K_max:=10;

 

Here the C and D species do not form. As KA1 rises we populate B.

MuPAD graphics

Total_R:=1;
Ka1:=variable;
Ka2:=5;
Kb1:=2;
K_max:=10;

 

Here, B is not formed in the beginning, C is 2xA and D is 5xC or 10xA.

 

As KA1 rises we create more B and reduce D. When KA1=10 we see the same amount of B and D so KB2=1

 

We derived:

K_B_2 = (K_A_2*K_B_1)/K_A_1

so  5*2/10=1 !!! Yes, the derivation of the model is correct.

 

 

MuPAD graphics

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Back to Contents

 

 

Conclusions

 

1. I analyzed analytical solutions for the U_R_RL system. They analytical solutions seem to work correctly.

 

 

Back to Contents