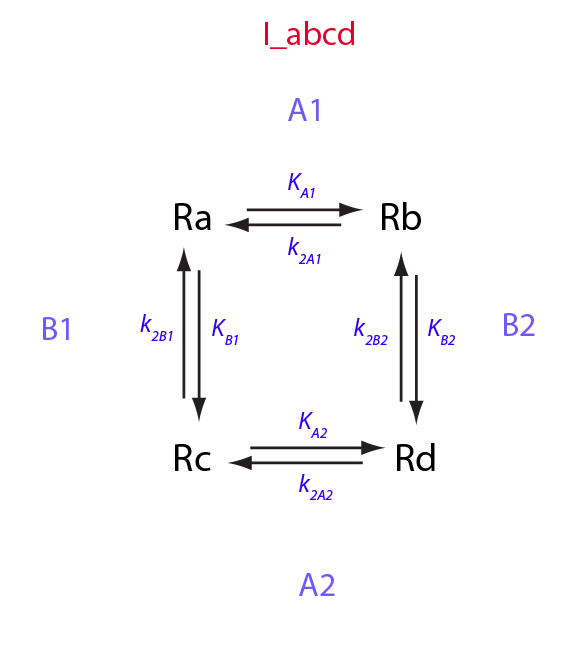
Derivation of equations for I_abcd model
Intramolecular isomerization between four forms

2. Derivation of a main equation
3. Define functions for equilibrium concentrations
4. Test if solution is meaningful
5. Check whether the solution satisfies all initial equation and conditions
6. Save results on disk for future use
In this notebook I will derive equations for the isomerization equilibrium between four species
Analysis will be done in I_abcd_analysis.mn
clean up workspace
reset()
Set path to save results into:
ProjectName:="I_abcd";
CurrentPath:="/Users/kovrigin/Documents/Workspace/Global Analysis/IDAP/Mathematical_models/Equilibrium_thermodynamic_models/I_abcd/";
![]()

Isomerization constants
These relationships serve as restraints for solve(), but not restrict these values in calculations!
K_A_1
K_A_1 ;
assume(K_A_1 > 0):
assumeAlso(K_A_1 , R_):
![]()
K_A_2
K_A_2 ;
assumeAlso(K_A_2 > 0):
assumeAlso(K_A_2 , R_):
![]()
K_B_1
K_B_1 ;
assumeAlso(K_B_1 > 0):
assumeAlso(K_B_1 , R_):
![]()
K_B_2 ---- this is chosen as a dependent constant
K_B_2 ;
assumeAlso(K_B_2 > 0):
assumeAlso(K_B_2 , R_):
![]()
Total concentrations
Rtot - total concentration of the molecule
Rtot;
assumeAlso(Rtot>0):
assumeAlso(Rtot,R_):
![]()
Common equilibrium concentrations
Raeq - equilibrium concentration of Ra form
Raeq;
assumeAlso(Raeq>0):
assumeAlso(Raeq<Rtot):
assumeAlso(Raeq,R_):
![]()
Rbeq - equilibrium concentration of Rb form
Rbeq;
assumeAlso(Rbeq>0):
assumeAlso(Rbeq<Rtot):
assumeAlso(Rbeq,R_):
![]()
Rceq - equilibrium concentration of Rc form
Rceq;
assumeAlso(Rceq>0):
assumeAlso(Rceq<Rtot):
assumeAlso(Rceq,R_):
![]()
Rdeq - equilibrium concentration of Rb form
Rdeq;
assumeAlso(Rdeq>0):
assumeAlso(Rdeq<Rtot):
assumeAlso(Rdeq,R_):
![]()
anames(Properties,User);
![]()
2. Derivation of a main equation
Total concentrations of the molecule
eq2_1:= Rtot = Raeq + Rbeq + Rceq + Rdeq
![]()
Write equilibrium thermodynamics equations
eq2_2:= K_A_1 = Rbeq / Raeq
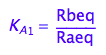
eq2_3:= K_A_2 = Rdeq / Rceq
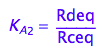
eq2_4:= K_B_1 = Rceq / Raeq
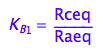
eq2_5:= K_B_2 = Rdeq / Rbeq
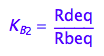
Express Raeq as a function of all constants and total concentrations
(K_B_2 is dependent, don't use it)
Express Rbeq
eq2_2;
solve(%,Rbeq);
%[1][1];
eq2_6:= Rbeq= %
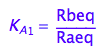
![piecewise([K_A_1*Raeq in Dom::Interval(0, Rtot), {K_A_1*Raeq}], [not K_A_1*Raeq in Dom::Interval(0, Rtot), {}])](I_abcd_derivation_images/math18.png)
![]()
![]()
Express Rdeq
eq2_3;
solve(%,Rdeq);
%[1][1];
eq2_7:= Rdeq= %
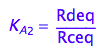
![piecewise([K_A_2*Rceq in Dom::Interval(0, Rtot), {K_A_2*Rceq}], [not K_A_2*Rceq in Dom::Interval(0, Rtot), {}])](I_abcd_derivation_images/math22.png)
![]()
![]()
Express Rceq
eq2_4;
solve(%,Rceq);
%[1][1];
eq2_8:= Rceq= %
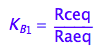
![piecewise([K_B_1*Raeq in Dom::Interval(0, Rtot), {K_B_1*Raeq}], [not K_B_1*Raeq in Dom::Interval(0, Rtot), {}])](I_abcd_derivation_images/math26.png)
![]()
![]()
Substitute to the mass balance equation
eq2_1;
% | eq2_6 | eq2_7 | eq2_8;
eq2_9:= %:
![]()
![]()
Express individual equilibrium concentrations
Express Raeq
eq2_9;
solve(%, Raeq);
eq2_10:= Raeq=%[1]
![]()
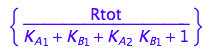
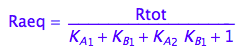
Express Rbeq
eq2_6;
% | eq2_10;
eq2_11:= %:
![]()
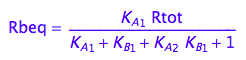
Express Rceq
eq2_8;
% | eq2_10;
eq2_12:= %:
![]()
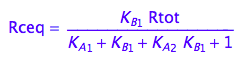
Express Rdeq
eq2_7;
% | eq2_12;
eq2_13:= %:
![]()
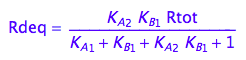
Express the dependent constant
eq2_5;
% | eq2_13 | eq2_11;
eq2_14:= %:
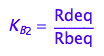
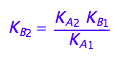
Summary of equations for all species
Independent parameters:
Rtot, K_A_1, K_A_2, K_B_1
![]()
Equilbrium concentrations:
[Ra]
eq2_10
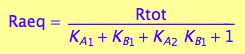
[Rb]
eq2_11
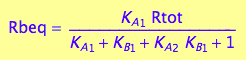
[Rc]
eq2_12
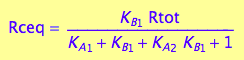
[Rd]
eq2_13
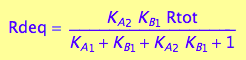
The dependent constant:
K_B_2
eq2_14
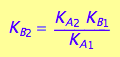
Generate functions
eq2_10;
fRaeq:= (Rtot, K_A_1, K_A_2, K_B_1) --> rhs(%)
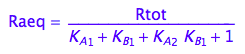

eq2_11;
fRbeq:= (Rtot, K_A_1, K_A_2, K_B_1) --> rhs(%)
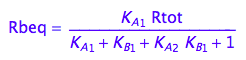
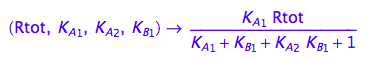
eq2_12;
fRceq:= (Rtot, K_A_1, K_A_2, K_B_1) --> rhs(%)
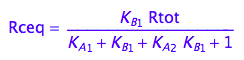
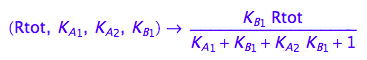
eq2_13;
fRdeq:= (Rtot, K_A_1, K_A_2, K_B_1) --> rhs(%)
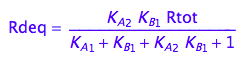
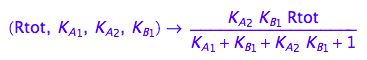
4. Test if solution is meaningful
Set some realistic values for constants:
Total_R:=1;
Ka1:=0.5;
Ka2:=0.5;
Kb1:=0.333;
![]()
![]()
![]()
![]()
Test that all equilibrium concentrations are positive values:
a:=fRaeq(Total_R, Ka1, Ka2, Kb1);
b:=fRbeq(Total_R, Ka1, Ka2, Kb1);
c:=fRceq(Total_R, Ka1, Ka2, Kb1);
d:=fRdeq(Total_R, Ka1, Ka2, Kb1);
if (a>0 and b>0 and c>0 and d>0
)
then
print(Unquoted,"Solution is meaningful.");
else
print(Unquoted,"WARNING!!!!");
print(Unquoted,"Solution is NOT meaningful: some concentrations become negative!");
end_if
![]()
![]()
![]()
![]()
Solution is meaningful.
5. Check whether the solution satisfies all initial equation and conditions
Here are all original independent
equations:
eq2_1;eq2_2;eq2_3;eq2_4;
![]()
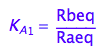
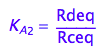
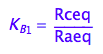
Test eq2_1
eq2_1;
% | eq2_10 | eq2_11 | eq2_12 | eq2_13 ;
normal(%);
bool(%)
![]()
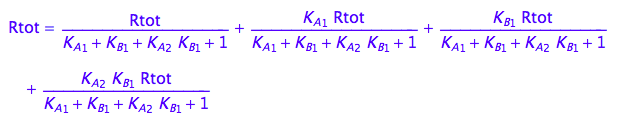
![]()
![]()
Test eq2_2
eq2_2;
% | eq2_10 | eq2_11 | eq2_12 | eq2_13 ;
normal(%);
bool(%)
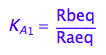
![]()
![]()
![]()
Test eq2_3
eq2_3;
% | eq2_10 | eq2_11 | eq2_12 | eq2_13 ;
normal(%);
bool(%)
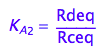
![]()
![]()
![]()
Test eq2_4
eq2_4;
% | eq2_10 | eq2_11 | eq2_12 | eq2_13 ;
normal(%);
bool(%)
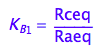
![]()
![]()
![]()
The found solution satisfies all original equations
5. Save results on disk for future use
(you can retrieve them later by executing: fread(filename,Quiet))
ProjectName
![]()
Eq_Raeq_I_abcd:= eq2_10;
Eq_Rbeq_I_abcd:= eq2_11;
Eq_Rceq_I_abcd:= eq2_12;
Eq_Rdeq_I_abcd:= eq2_13;
Eq_KB2_I_abcd:= eq2_14;
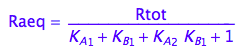
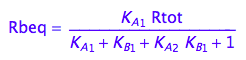
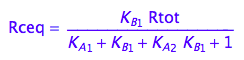
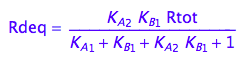
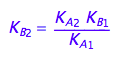
Reassign function names
fRaeq_I_abcd:=fRaeq:
fRbeq_I_abcd:=fRbeq:
fRceq_I_abcd:=fRceq:
fRdeq_I_abcd:=fRdeq:
filename:=CurrentPath.ProjectName.".mb";
write(filename,Eq_Raeq_I_abcd,Eq_Rbeq_I_abcd, Eq_Rceq_I_abcd, Eq_Rdeq_I_abcd, Eq_KB2_I_abcd,fRaeq_I_abcd,fRbeq_I_abcd,fRceq_I_abcd,fRdeq_I_abcd)

Conclusions
1. I derived analytical solutions for the I_ab system
TEMPLATE