ProjectName:="LRIM_U_L";
CurrentPath:="/Users/kovrigin/Documents/Workspace/Data/Data.XV/EKM16.Analysis_of_multistep_kinetic_mechanisms/Equilibria/";
![]()
![]()
Analysis of U-L model
A: R + L <=> RL
B: L <=> L*
2. Derivation of working equation
3. Express concentrations of equilibrium species in terms of a found solution
4. Define functions for equilibrium concentrations
5. Test if solution is meaningful
6. Check whether the solution satisfies all initial equation and conditions
7. Save results on disk for future use
In this notebook I will write out equations for equilibrium concentrations and either solve them or generate expressions for numeric solutions for a number of models derived in /Users/kovrigin/Documents/Workspace/Data/Data.XV/EKM16.Analysis_of_multistep_kinetic_mechanisms/LRIM/Specific_models/Models.pdf
clean up workspace
reset()
Set path to save results into:
ProjectName:="LRIM_U_L";
CurrentPath:="/Users/kovrigin/Documents/Workspace/Data/Data.XV/EKM16.Analysis_of_multistep_kinetic_mechanisms/Equilibria/";
![]()
![]()
Binding constants:
All binding constants I am using are formation constants so I denote them all as Ka and add a label for the transition.
K_a_A - monomer-ligand interaction
K_a_A;
assume(K_a_A >= 0):
assumeAlso(K_a_A, R_):
![]()
K_a_B - Ligand isomerization constant
K_a_B;
assumeAlso(K_a_B>=0):
assumeAlso(K_a_B,R_):
![]()
Total concentrations
Rtot - total concentration of the receptor
Rtot;
assumeAlso(Rtot>=0):
assumeAlso(Rtot,R_):
![]()
Ltot - total concentration of a ligand
Ltot;
assumeAlso(Ltot>=0):
assumeAlso(Ltot,R_):
![]()
Common equilibrium concentrations
Req - equilibrium concentration of a receptor monomer
Req;
assumeAlso(Req>=0):
assumeAlso(Req<=Rtot):
assumeAlso(Req,R_):
![]()
Leq - equilibrium concentration of a receptor monomer
Leq;
assumeAlso(Leq>=0):
assumeAlso(Leq<=Ltot):
assumeAlso(Leq,R_):
![]()
RLeq - equilibrium concentration of a receptor monomer
RLeq;
assumeAlso(RLeq>=0):
assumeAlso(RLeq<=Rtot):
assumeAlso(RLeq,R_):
![]()
Other species will be defined in the sections of specific models.
anames(All,User);
anames(Properties,User);

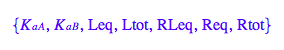
2. Derivation of working equation
U-L is a model with a ligand isomerization such that only one of the isomers binds a receptor.
Working equation: I will try to express analytical [L] from equation for a total concentration of a receptor or use it for numeric solution if analytical is not possible
[L*] - equilibrium concentration of a non-binding L-isomer
Lstareq;
assumeAlso(Lstareq>=0):
assumeAlso(Lstareq<=Ltot):
assumeAlso(Lstareq,R_):
![]()
Total concentrations of protein and a ligand
eq2_1:= Rtot = Req + RLeq;
eq2_2:= Ltot = Leq + RLeq + Lstareq;
![]()
![]()
Transition A: Equilibrium constant of ligand binding
eq2_3:= K_a_A = RLeq / (Req*Leq);
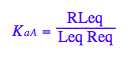
Transition B: Equilibrium constant of isomerization
eq2_4:= K_a_B = Lstareq/Leq;
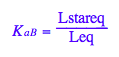
Let's get rid of [Lstareq]
solve(eq2_4,Lstareq);
eq2_5:= Lstareq = %[2][1]
![]()
Let's get rid of [R]
solve(eq2_3,Req);
eq2_6:= Req = %[2][1]
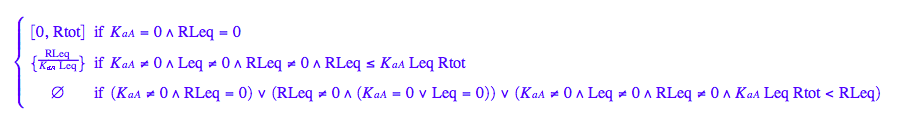
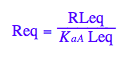
Let's get rid of [RL]
solve(eq2_2,RLeq);
%[1][1] ;
% | eq2_5;
eq2_7:= RLeq = %
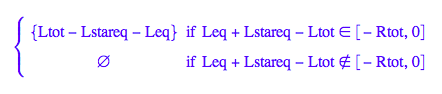
![]()
![]()
![]()
Substitute
eq2_1 | eq2_5;
% | eq2_6;
% | eq2_7;
eq2_8:= %;
![]()
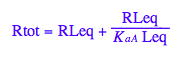
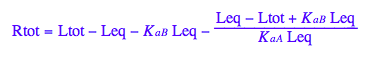
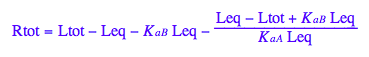
Final equation for [L] in terms of all constants
eq2_8

For the sake of my speed - use numerical solutions leaving analytical for future analysis.
Solve it for [L]
solutions2:=solve(eq2_8, Leq)

Analytically soluble: I still go to Matlab
Summary of equations for equilibrium concentrations:
eq2_8

eq2_7;
![]()
eq2_6;
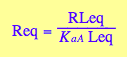
eq2_5;
![]()
1. I derived a formula for numeric solution