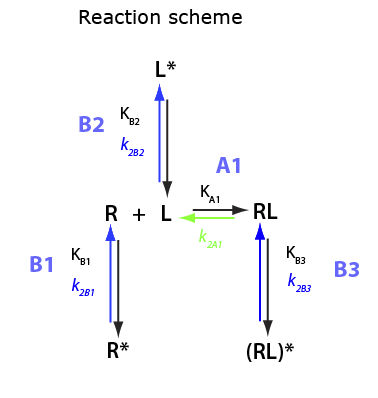
U-R-L-RL
Derivation of equilibrium thermodynamic equations for U-R-L-RL system: isomerization in both reactants and in the complex.
NOTE: ANALYTICAL SOLUTION WAS OBTAINED

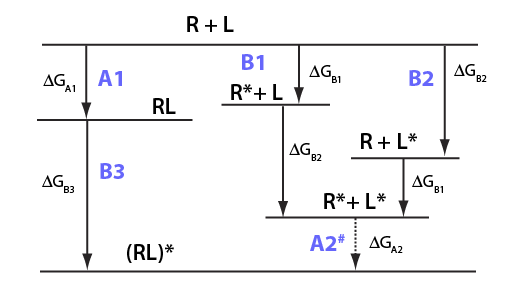
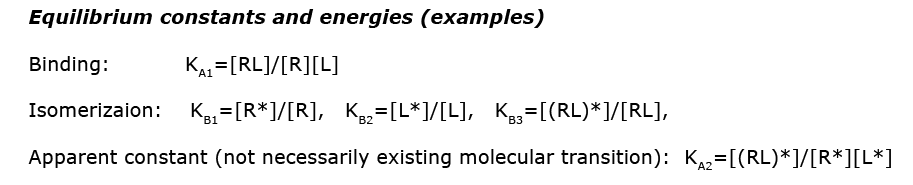
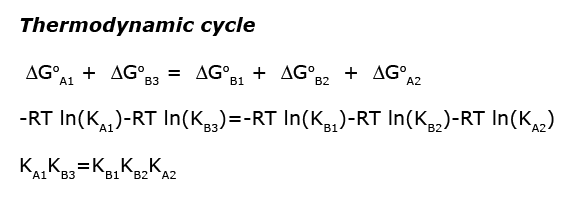
Images from: /Users/kovrigin/Documents/Workspace/Global Analysis/code_development/Mathematical_models/Equilibrium thermodynamic models/U-R-L-RL/U-R-L-RL.ai
2. Basic equilibrium equations
3. Derivation of equations for equilibrium concentrations
4. Prepare equations for a numeric solution
5. Save results on disk for future use
Here I will derive equations for equilibrium when R, L and RL undergo isomerization. We do not specify whether isomers are able to bind to each other (this is a matter of kinetic modeling).
clean up workspace
reset()
Set path to save results into:
ProjectName:="U-R-L-RL";
CurrentPath:="/Users/kovrigin/Documents/Workspace/Global Analysis/code_development/Mathematical_models/Equilibrium_thermodynamic_models/U-R-L-RL/";
![]()

Binding and isomerization constants
All binding constants I am using are association constants.
These relationships serve as restraints for solve(), but not restrict these values in calculations!
K_A_1
K_A_1 ;
assumeAlso(K_A_1 > 0):
assumeAlso(K_A_1 , R_)
![]()
K_B_1
K_B_1 ;
assumeAlso(K_B_1 > 0):
assumeAlso(K_B_1 , R_):
![]()
K_B_2
K_B_2 ;
assumeAlso(K_B_2 > 0):
assumeAlso(K_B_2 , R_):
![]()
K_B_3
K_B_3 ;
assumeAlso(K_B_3 > 0):
assumeAlso(K_B_3 , R_):
![]()
Total concentrations
Rtot - total concentration of the receptor
Rtot;
assumeAlso(Rtot>0):
assumeAlso(Rtot,R_):
![]()
Ltot - total concentration of the ligand
Ltot;
assumeAlso(Ltot>0):
assumeAlso(Ltot,R_):
![]()
Equilibrium concentrations
Req - equilibrium concentration of the first receptor
Req;
assumeAlso(Req>0):
assumeAlso(Req<Rtot):
assumeAlso(Req,R_):
![]()
Rstareq - equilibrium concentration of the second receptor
Rstareq;
assumeAlso(Rstareq>0):
assumeAlso(Rstareq<Rtot):
assumeAlso(Rstareq,R_):
![]()
Leq - equilibrium concentration of a free ligand
Leq;
assumeAlso(Leq>0):
assumeAlso(Leq<Ltot):
assumeAlso(Leq,R_):
![]()
Lstareq - equilibrium concentration of a free ligand
Lstareq;
assumeAlso(Lstareq>0):
assumeAlso(Lstareq<Ltot):
assumeAlso(Lstareq,R_):
![]()
RLeq - equilibrium concentration of the first receptor-ligand complex
RLeq;
assumeAlso(RLeq>0):
assumeAlso(RLeq<Rtot):
assumeAlso(RLeq,R_):
![]()
RLstareq - equilibrium concentration of the first receptor-ligand complex
RLstareq;
assumeAlso(RLstareq>0):
assumeAlso(RLstareq<Rtot):
assumeAlso(RLstareq,R_):
![]()
Check what we defined
anames(Properties,User);
![]()
2. Basic equilibrium equations
Mass conservation equations
eq2_1:= Rtot = Req + Rstareq + RLeq + RLstareq;
eq2_2:= Ltot = Leq + Lstareq + RLeq + RLstareq;
![]()
![]()
Equilibrium constants
eq2_3:= K_A_1 = RLeq / (Req*Leq);
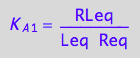
eq2_4:= K_B_1 = Rstareq/Req

eq2_5:= K_B_2 = Lstareq/Leq

eq2_6:= K_B_3 = RLstareq/RLeq

3. Derivation of equations for equilibrium concentrations
Express Leq as a function of all constants and total concentrations. If insoluble ---express Rtot=f(Leq and all constants).
Express the highest-order bound species first:
(RL)*
eq2_6;
solve(%,RLstareq):
%[1][1]:
eq3_1:= RLstareq=%

![]()
Substitute into the mass conservation laws:
eq2_1;
% | eq3_1:
eq3_2:= %
![]()
![]()
eq2_2;
% | eq3_1:
eq3_3:= %
![]()
![]()
Express next-lower bound order species:
RL
eq2_3;
solve(%,RLeq):
%[1][1]:
eq3_4:= RLeq = %
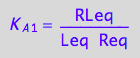
![]()
Substitute into new mass-conservation laws
eq3_2;
% | eq3_4:
eq3_5:= %
![]()
![]()
eq3_3;
% | eq3_4:
eq3_6:= %
![]()
![]()
Express isomers
R*
eq2_4;
solve(%,Rstareq):
%[1][1]:
eq3_7:= Rstareq = %

![]()
-> conservation laws
eq3_5;
% | eq3_7:
eq3_8:= %
![]()
![]()
L*
eq2_5;
solve(%, Lstareq):
%[1][1]:
eq3_9:= Lstareq = %

![]()
-> conservation laws
eq3_6;
% | eq3_9:
eq3_10:= %
![]()
![]()
Aim to obtain Rtot=f(Leq, constants) function
express Req
eq3_10;
solve(%,Req):
%[1][1]:
eq3_11:= Req = %
![]()

substitute in Rtot=f(...)
eq3_8;
% | eq3_11;
temp1:=%[2];
temp2:=Simplify(%);
// test
temp1=temp2;
Simplify(%);
// Assemble a final equation
eq3_12:= Rtot =temp2
![]()


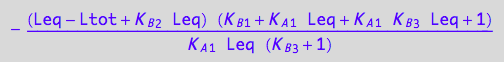

![]()

Attempt to solve for Leq
solution3_12:=solve(eq3_12, Leq)
![piecewise([2*Ltot*Rtot*K_A_1^2*K_B_3^2 + 4*Ltot*Rtot*K_A_1^2*K_B_3 + 2*Ltot*Rtot*K_A_1^2 <= K_A_1^2*K_B_3^2*Ltot^2 + K_A_1^2*K_B_3^2*Rtot^2 + 2*K_A_1^2*K_B_3*Ltot^2 + 2*K_A_1^2*K_B_3*Rtot^2 + K_A_1^2*Ltot^2 + K_A_1^2*Rtot^2 + 2*K_A_1*K_B_1*K_B_2*K_B_3*Rtot + 2*K_A_1*K_B_1*K_B_2*Rtot + 2*K_A_1*K_B_1*K_B_3*Rtot + 2*K_A_1*K_B_1*Rtot + 2*K_A_1*K_B_2*K_B_3*Rtot + 2*K_A_1*K_B_2*Rtot + 2*K_A_1*K_B_3*Rtot + 2*K_A_1*Rtot + K_B_1^2*K_B_2^2 + 2*K_B_1^2*K_B_2 + K_B_1^2 + 2*K_B_1*K_B_2^2 + 4*K_B_1*K_B_2 + 2*K_B_1 + K_B_2^2 + 2*K_B_2 + 1 and (K_A_1^2*K_B_3^2*Ltot^2 - 2*K_A_1^2*K_B_3^2*Ltot*Rtot + K_A_1^2*K_B_3^2*Rtot^2 + 2*K_A_1^2*K_B_3*Ltot^2 - 4*K_A_1^2*K_B_3*Ltot*Rtot + 2*K_A_1^2*K_B_3*Rtot^2 + K_A_1^2*Ltot^2 - 2*K_A_1^2*Ltot*Rtot + K_A_1^2*Rtot^2 + 2*K_A_1*K_B_1*K_B_2*K_B_3*Ltot + 2*K_A_1*K_B_1*K_B_2*K_B_3*Rtot + 2*K_A_1*K_B_1*K_B_2*Ltot + 2*K_A_1*K_B_1*K_B_2*Rtot + 2*K_A_1*K_B_1*K_B_3*Ltot + 2*K_A_1*K_B_1*K_B_3*Rtot + 2*K_A_1*K_B_1*Ltot + 2*K_A_1*K_B_1*Rtot + 2*K_A_1*K_B_2*K_B_3*Ltot + 2*K_A_1*K_B_2*K_B_3*Rtot + 2*K_A_1*K_B_2*Ltot + 2*K_A_1*K_B_2*Rtot + 2*K_A_1*K_B_3*Ltot + 2*K_A_1*K_B_3*Rtot + 2*K_A_1*Ltot + 2*K_A_1*Rtot + K_B_1^2*K_B_2^2 + 2*K_B_1^2*K_B_2 + K_B_1^2 + 2*K_B_1*K_B_2^2 + 4*K_B_1*K_B_2 + 2*K_B_1 + K_B_2^2 + 2*K_B_2 + 1)^(1/2) + K_A_1*Ltot + K_A_1*K_B_3*Ltot = K_B_1 + K_B_2 + K_B_1*K_B_2 + K_A_1*Rtot + K_A_1*K_B_3*Rtot + 1 and K_B_1 + K_B_2 + (K_A_1^2*K_B_3^2*Ltot^2 - 2*K_A_1^2*K_B_3^2*Ltot*Rtot + K_A_1^2*K_B_3^2*Rtot^2 + 2*K_A_1^2*K_B_3*Ltot^2 - 4*K_A_1^2*K_B_3*Ltot*Rtot + 2*K_A_1^2*K_B_3*Rtot^2 + K_A_1^2*Ltot^2 - 2*K_A_1^2*Ltot*Rtot + K_A_1^2*Rtot^2 + 2*K_A_1*K_B_1*K_B_2*K_B_3*Ltot + 2*K_A_1*K_B_1*K_B_2*K_B_3*Rtot + 2*K_A_1*K_B_1*K_B_2*Ltot + 2*K_A_1*K_B_1*K_B_2*Rtot + 2*K_A_1*K_B_1*K_B_3*Ltot + 2*K_A_1*K_B_1*K_B_3*Rtot + 2*K_A_1*K_B_1*Ltot + 2*K_A_1*K_B_1*Rtot + 2*K_A_1*K_B_2*K_B_3*Ltot + 2*K_A_1*K_B_2*K_B_3*Rtot + 2*K_A_1*K_B_2*Ltot + 2*K_A_1*K_B_2*Rtot + 2*K_A_1*K_B_3*Ltot + 2*K_A_1*K_B_3*Rtot + 2*K_A_1*Ltot + 2*K_A_1*Rtot + K_B_1^2*K_B_2^2 + 2*K_B_1^2*K_B_2 + K_B_1^2 + 2*K_B_1*K_B_2^2 + 4*K_B_1*K_B_2 + 2*K_B_1 + K_B_2^2 + 2*K_B_2 + 1)^(1/2) + K_B_1*K_B_2 + K_A_1*Rtot + K_A_1*K_B_3*Rtot + 1 <> K_A_1*Ltot + K_A_1*K_B_3*Ltot and -(K_B_1 + K_B_2 + (K_A_1^2*K_B_3^2*Ltot^2 - 2*K_A_1^2*K_B_3^2*Ltot*Rtot + K_A_1^2*K_B_3^2*Rtot^2 + 2*K_A_1^2*K_B_3*Ltot^2 - 4*K_A_1^2*K_B_3*Ltot*Rtot + 2*K_A_1^2*K_B_3*Rtot^2 + K_A_1^2*Ltot^2 - 2*K_A_1^2*Ltot*Rtot + K_A_1^2*Rtot^2 + 2*K_A_1*K_B_1*K_B_2*K_B_3*Rtot + 2*K_A_1*K_B_1*K_B_2*Rtot + 2*K_A_1*K_B_1*K_B_3*Rtot + 2*K_A_1*K_B_1*Rtot + 2*K_A_1*K_B_2*K_B_3*Rtot + 2*K_A_1*K_B_2*Rtot + 2*K_A_1*K_B_3*Rtot + 2*K_A_1*Rtot + K_B_1^2*K_B_2^2 + 2*K_B_1^2*K_B_2 + K_B_1^2 + 2*K_B_1*K_B_2^2 + 4*K_B_1*K_B_2 + 2*K_B_1 + K_B_2^2 + 2*K_B_2 + 1)^(1/2) + K_B_1*K_B_2 - K_A_1*Ltot + K_A_1*Rtot - K_A_1*K_B_3*Ltot + K_A_1*K_B_3*Rtot + 1)/(2*K_A_1*(K_B_2 + K_B_3 + K_B_2*K_B_3 + 1)) < Ltot and (K_B_1 + K_B_2 + (K_A_1^2*K_B_3^2*Ltot^2 - 2*K_A_1^2*K_B_3^2*Ltot*Rtot + K_A_1^2*K_B_3^2*Rtot^2 + 2*K_A_1^2*K_B_3*Ltot^2 - 4*K_A_1^2*K_B_3*Ltot*Rtot + 2*K_A_1^2*K_B_3*Rtot^2 + K_A_1^2*Ltot^2 - 2*K_A_1^2*Ltot*Rtot + K_A_1^2*Rtot^2 + 2*K_A_1*K_B_1*K_B_2*K_B_3*Rtot + 2*K_A_1*K_B_1*K_B_2*Rtot + 2*K_A_1*K_B_1*K_B_3*Rtot + 2*K_A_1*K_B_1*Rtot + 2*K_A_1*K_B_2*K_B_3*Rtot + 2*K_A_1*K_B_2*Rtot + 2*K_A_1*K_B_3*Rtot + 2*K_A_1*Rtot + K_B_1^2*K_B_2^2 + 2*K_B_1^2*K_B_2 + K_B_1^2 + 2*K_B_1*K_B_2^2 + 4*K_B_1*K_B_2 + 2*K_B_1 + K_B_2^2 + 2*K_B_2 + 1)^(1/2) + K_B_1*K_B_2 - K_A_1*Ltot + K_A_1*Rtot - K_A_1*K_B_3*Ltot + K_A_1*K_B_3*Rtot + 1)/(K_B_2 + K_B_3 + K_B_2*K_B_3 + 1) < 0, {-(K_B_1 + K_B_2 + (K_A_1^2*K_B_3^2*Ltot^2 - 2*K_A_1^2*K_B_3^2*Ltot*Rtot + K_A_1^2*K_B_3^2*Rtot^2 + 2*K_A_1^2*K_B_3*Ltot^2 - 4*K_A_1^2*K_B_3*Ltot*Rtot + 2*K_A_1^2*K_B_3*Rtot^2 + K_A_1^2*Ltot^2 - 2*K_A_1^2*Ltot*Rtot + K_A_1^2*Rtot^2 + 2*K_A_1*K_B_1*K_B_2*K_B_3*Rtot + 2*K_A_1*K_B_1*K_B_2*Rtot + 2*K_A_1*K_B_1*K_B_3*Rtot + 2*K_A_1*K_B_1*Rtot + 2*K_A_1*K_B_2*K_B_3*Rtot + 2*K_A_1*K_B_2*Rtot + 2*K_A_1*K_B_3*Rtot + 2*K_A_1*Rtot + K_B_1^2*K_B_2^2 + 2*K_B_1^2*K_B_2 + K_B_1^2 + 2*K_B_1*K_B_2^2 + 4*K_B_1*K_B_2 + 2*K_B_1 + K_B_2^2 + 2*K_B_2 + 1)^(1/2) + K_B_1*K_B_2 - K_A_1*Ltot + K_A_1*Rtot - K_A_1*K_B_3*Ltot + K_A_1*K_B_3*Rtot + 1)/(2*(K_A_1 + K_A_1*K_B_2 + K_A_1*K_B_3 + K_A_1*K_B_2*K_B_3))}], [-(K_B_1 + K_B_2 - (K_A_1^2*K_B_3^2*Ltot^2 - 2*K_A_1^2*K_B_3^2*Ltot*Rtot + K_A_1^2*K_B_3^2*Rtot^2 + 2*K_A_1^2*K_B_3*Ltot^2 - 4*K_A_1^2*K_B_3*Ltot*Rtot + 2*K_A_1^2*K_B_3*Rtot^2 + K_A_1^2*Ltot^2 - 2*K_A_1^2*Ltot*Rtot + K_A_1^2*Rtot^2 + 2*K_A_1*K_B_1*K_B_2*K_B_3*Rtot + 2*K_A_1*K_B_1*K_B_2*Rtot + 2*K_A_1*K_B_1*K_B_3*Rtot + 2*K_A_1*K_B_1*Rtot + 2*K_A_1*K_B_2*K_B_3*Rtot + 2*K_A_1*K_B_2*Rtot + 2*K_A_1*K_B_3*Rtot + 2*K_A_1*Rtot + K_B_1^2*K_B_2^2 + 2*K_B_1^2*K_B_2 + K_B_1^2 + 2*K_B_1*K_B_2^2 + 4*K_B_1*K_B_2 + 2*K_B_1 + K_B_2^2 + 2*K_B_2 + 1)^(1/2) + K_B_1*K_B_2 - K_A_1*Ltot + K_A_1*Rtot - K_A_1*K_B_3*Ltot + K_A_1*K_B_3*Rtot + 1)/(2*K_A_1*(K_B_2 + K_B_3 + K_B_2*K_B_3 + 1)) < Ltot and (K_B_1 + K_B_2 - (K_A_1^2*K_B_3^2*Ltot^2 - 2*K_A_1^2*K_B_3^2*Ltot*Rtot + K_A_1^2*K_B_3^2*Rtot^2 + 2*K_A_1^2*K_B_3*Ltot^2 - 4*K_A_1^2*K_B_3*Ltot*Rtot + 2*K_A_1^2*K_B_3*Rtot^2 + K_A_1^2*Ltot^2 - 2*K_A_1^2*Ltot*Rtot + K_A_1^2*Rtot^2 + 2*K_A_1*K_B_1*K_B_2*K_B_3*Rtot + 2*K_A_1*K_B_1*K_B_2*Rtot + 2*K_A_1*K_B_1*K_B_3*Rtot + 2*K_A_1*K_B_1*Rtot + 2*K_A_1*K_B_2*K_B_3*Rtot + 2*K_A_1*K_B_2*Rtot + 2*K_A_1*K_B_3*Rtot + 2*K_A_1*Rtot + K_B_1^2*K_B_2^2 + 2*K_B_1^2*K_B_2 + K_B_1^2 + 2*K_B_1*K_B_2^2 + 4*K_B_1*K_B_2 + 2*K_B_1 + K_B_2^2 + 2*K_B_2 + 1)^(1/2) + K_B_1*K_B_2 - K_A_1*Ltot + K_A_1*Rtot - K_A_1*K_B_3*Ltot + K_A_1*K_B_3*Rtot + 1)/(K_B_2 + K_B_3 + K_B_2*K_B_3 + 1) < 0 and 2*Ltot*Rtot*K_A_1^2*K_B_3^2 + 4*Ltot*Rtot*K_A_1^2*K_B_3 + 2*Ltot*Rtot*K_A_1^2 <= K_A_1^2*K_B_3^2*Ltot^2 + K_A_1^2*K_B_3^2*Rtot^2 + 2*K_A_1^2*K_B_3*Ltot^2 + 2*K_A_1^2*K_B_3*Rtot^2 + K_A_1^2*Ltot^2 + K_A_1^2*Rtot^2 + 2*K_A_1*K_B_1*K_B_2*K_B_3*Rtot + 2*K_A_1*K_B_1*K_B_2*Rtot + 2*K_A_1*K_B_1*K_B_3*Rtot + 2*K_A_1*K_B_1*Rtot + 2*K_A_1*K_B_2*K_B_3*Rtot + 2*K_A_1*K_B_2*Rtot + 2*K_A_1*K_B_3*Rtot + 2*K_A_1*Rtot + K_B_1^2*K_B_2^2 + 2*K_B_1^2*K_B_2 + K_B_1^2 + 2*K_B_1*K_B_2^2 + 4*K_B_1*K_B_2 + 2*K_B_1 + K_B_2^2 + 2*K_B_2 + 1 and K_B_1 + K_B_2 + (K_A_1^2*K_B_3^2*Ltot^2 - 2*K_A_1^2*K_B_3^2*Ltot*Rtot + K_A_1^2*K_B_3^2*Rtot^2 + 2*K_A_1^2*K_B_3*Ltot^2 - 4*K_A_1^2*K_B_3*Ltot*Rtot + 2*K_A_1^2*K_B_3*Rtot^2 + K_A_1^2*Ltot^2 - 2*K_A_1^2*Ltot*Rtot + K_A_1^2*Rtot^2 + 2*K_A_1*K_B_1*K_B_2*K_B_3*Ltot + 2*K_A_1*K_B_1*K_B_2*K_B_3*Rtot + 2*K_A_1*K_B_1*K_B_2*Ltot + 2*K_A_1*K_B_1*K_B_2*Rtot + 2*K_A_1*K_B_1*K_B_3*Ltot + 2*K_A_1*K_B_1*K_B_3*Rtot + 2*K_A_1*K_B_1*Ltot + 2*K_A_1*K_B_1*Rtot + 2*K_A_1*K_B_2*K_B_3*Ltot + 2*K_A_1*K_B_2*K_B_3*Rtot + 2*K_A_1*K_B_2*Ltot + 2*K_A_1*K_B_2*Rtot + 2*K_A_1*K_B_3*Ltot + 2*K_A_1*K_B_3*Rtot + 2*K_A_1*Ltot + 2*K_A_1*Rtot + K_B_1^2*K_B_2^2 + 2*K_B_1^2*K_B_2 + K_B_1^2 + 2*K_B_1*K_B_2^2 + 4*K_B_1*K_B_2 + 2*K_B_1 + K_B_2^2 + 2*K_B_2 + 1)^(1/2) + K_B_1*K_B_2 + K_A_1*Rtot + K_A_1*K_B_3*Rtot + 1 = K_A_1*Ltot + K_A_1*K_B_3*Ltot and (K_A_1^2*K_B_3^2*Ltot^2 - 2*K_A_1^2*K_B_3^2*Ltot*Rtot + K_A_1^2*K_B_3^2*Rtot^2 + 2*K_A_1^2*K_B_3*Ltot^2 - 4*K_A_1^2*K_B_3*Ltot*Rtot + 2*K_A_1^2*K_B_3*Rtot^2 + K_A_1^2*Ltot^2 - 2*K_A_1^2*Ltot*Rtot + K_A_1^2*Rtot^2 + 2*K_A_1*K_B_1*K_B_2*K_B_3*Ltot + 2*K_A_1*K_B_1*K_B_2*K_B_3*Rtot + 2*K_A_1*K_B_1*K_B_2*Ltot + 2*K_A_1*K_B_1*K_B_2*Rtot + 2*K_A_1*K_B_1*K_B_3*Ltot + 2*K_A_1*K_B_1*K_B_3*Rtot + 2*K_A_1*K_B_1*Ltot + 2*K_A_1*K_B_1*Rtot + 2*K_A_1*K_B_2*K_B_3*Ltot + 2*K_A_1*K_B_2*K_B_3*Rtot + 2*K_A_1*K_B_2*Ltot + 2*K_A_1*K_B_2*Rtot + 2*K_A_1*K_B_3*Ltot + 2*K_A_1*K_B_3*Rtot + 2*K_A_1*Ltot + 2*K_A_1*Rtot + K_B_1^2*K_B_2^2 + 2*K_B_1^2*K_B_2 + K_B_1^2 + 2*K_B_1*K_B_2^2 + 4*K_B_1*K_B_2 + 2*K_B_1 + K_B_2^2 + 2*K_B_2 + 1)^(1/2) + K_A_1*Ltot + K_A_1*K_B_3*Ltot <> K_B_1 + K_B_2 + K_B_1*K_B_2 + K_A_1*Rtot + K_A_1*K_B_3*Rtot + 1, {-(K_B_1 + K_B_2 - (K_A_1^2*K_B_3^2*Ltot^2 - 2*K_A_1^2*K_B_3^2*Ltot*Rtot + K_A_1^2*K_B_3^2*Rtot^2 + 2*K_A_1^2*K_B_3*Ltot^2 - 4*K_A_1^2*K_B_3*Ltot*Rtot + 2*K_A_1^2*K_B_3*Rtot^2 + K_A_1^2*Ltot^2 - 2*K_A_1^2*Ltot*Rtot + K_A_1^2*Rtot^2 + 2*K_A_1*K_B_1*K_B_2*K_B_3*Rtot + 2*K_A_1*K_B_1*K_B_2*Rtot + 2*K_A_1*K_B_1*K_B_3*Rtot + 2*K_A_1*K_B_1*Rtot + 2*K_A_1*K_B_2*K_B_3*Rtot + 2*K_A_1*K_B_2*Rtot + 2*K_A_1*K_B_3*Rtot + 2*K_A_1*Rtot + K_B_1^2*K_B_2^2 + 2*K_B_1^2*K_B_2 + K_B_1^2 + 2*K_B_1*K_B_2^2 + 4*K_B_1*K_B_2 + 2*K_B_1 + K_B_2^2 + 2*K_B_2 + 1)^(1/2) + K_B_1*K_B_2 - K_A_1*Ltot + K_A_1*Rtot - K_A_1*K_B_3*Ltot + K_A_1*K_B_3*Rtot + 1)/(2*(K_A_1 + K_A_1*K_B_2 + K_A_1*K_B_3 + K_A_1*K_B_2*K_B_3))}], [2*Ltot*Rtot*K_A_1^2*K_B_3^2 + 4*Ltot*Rtot*K_A_1^2*K_B_3 + 2*Ltot*Rtot*K_A_1^2 <= K_A_1^2*K_B_3^2*Ltot^2 + K_A_1^2*K_B_3^2*Rtot^2 + 2*K_A_1^2*K_B_3*Ltot^2 + 2*K_A_1^2*K_B_3*Rtot^2 + K_A_1^2*Ltot^2 + K_A_1^2*Rtot^2 + 2*K_A_1*K_B_1*K_B_2*K_B_3*Ltot + 2*K_A_1*K_B_1*K_B_2*K_B_3*Rtot + 2*K_A_1*K_B_1*K_B_2*Ltot + 2*K_A_1*K_B_1*K_B_2*Rtot + 2*K_A_1*K_B_1*K_B_3*Ltot + 2*K_A_1*K_B_1*K_B_3*Rtot + 2*K_A_1*K_B_1*Ltot + 2*K_A_1*K_B_1*Rtot + 2*K_A_1*K_B_2*K_B_3*Ltot + 2*K_A_1*K_B_2*K_B_3*Rtot + 2*K_A_1*K_B_2*Ltot + 2*K_A_1*K_B_2*Rtot + 2*K_A_1*K_B_3*Ltot + 2*K_A_1*K_B_3*Rtot + 2*K_A_1*Ltot + 2*K_A_1*Rtot + K_B_1^2*K_B_2^2 + 2*K_B_1^2*K_B_2 + K_B_1^2 + 2*K_B_1*K_B_2^2 + 4*K_B_1*K_B_2 + 2*K_B_1 + K_B_2^2 + 2*K_B_2 + 1 and -(K_B_1 + K_B_2 + (K_A_1^2*K_B_3^2*Ltot^2 - 2*K_A_1^2*K_B_3^2*Ltot*Rtot + K_A_1^2*K_B_3^2*Rtot^2 + 2*K_A_1^2*K_B_3*Ltot^2 - 4*K_A_1^2*K_B_3*Ltot*Rtot + 2*K_A_1^2*K_B_3*Rtot^2 + K_A_1^2*Ltot^2 - 2*K_A_1^2*Ltot*Rtot + K_A_1^2*Rtot^2 + 2*K_A_1*K_B_1*K_B_2*K_B_3*Ltot + 2*K_A_1*K_B_1*K_B_2*K_B_3*Rtot + 2*K_A_1*K_B_1*K_B_2*Ltot + 2*K_A_1*K_B_1*K_B_2*Rtot + 2*K_A_1*K_B_1*K_B_3*Ltot + 2*K_A_1*K_B_1*K_B_3*Rtot + 2*K_A_1*K_B_1*Ltot + 2*K_A_1*K_B_1*Rtot + 2*K_A_1*K_B_2*K_B_3*Ltot + 2*K_A_1*K_B_2*K_B_3*Rtot + 2*K_A_1*K_B_2*Ltot + 2*K_A_1*K_B_2*Rtot + 2*K_A_1*K_B_3*Ltot + 2*K_A_1*K_B_3*Rtot + 2*K_A_1*Ltot + 2*K_A_1*Rtot + K_B_1^2*K_B_2^2 + 2*K_B_1^2*K_B_2 + K_B_1^2 + 2*K_B_1*K_B_2^2 + 4*K_B_1*K_B_2 + 2*K_B_1 + K_B_2^2 + 2*K_B_2 + 1)^(1/2) + K_B_1*K_B_2 - K_A_1*Ltot + K_A_1*Rtot - K_A_1*K_B_3*Ltot + K_A_1*K_B_3*Rtot + 1)/(2*K_A_1*(K_B_2 + K_B_3 + K_B_2*K_B_3 + 1)) < Ltot and (K_B_1 + K_B_2 + (K_A_1^2*K_B_3^2*Ltot^2 - 2*K_A_1^2*K_B_3^2*Ltot*Rtot + K_A_1^2*K_B_3^2*Rtot^2 + 2*K_A_1^2*K_B_3*Ltot^2 - 4*K_A_1^2*K_B_3*Ltot*Rtot + 2*K_A_1^2*K_B_3*Rtot^2 + K_A_1^2*Ltot^2 - 2*K_A_1^2*Ltot*Rtot + K_A_1^2*Rtot^2 + 2*K_A_1*K_B_1*K_B_2*K_B_3*Ltot + 2*K_A_1*K_B_1*K_B_2*K_B_3*Rtot + 2*K_A_1*K_B_1*K_B_2*Ltot + 2*K_A_1*K_B_1*K_B_2*Rtot + 2*K_A_1*K_B_1*K_B_3*Ltot + 2*K_A_1*K_B_1*K_B_3*Rtot + 2*K_A_1*K_B_1*Ltot + 2*K_A_1*K_B_1*Rtot + 2*K_A_1*K_B_2*K_B_3*Ltot + 2*K_A_1*K_B_2*K_B_3*Rtot + 2*K_A_1*K_B_2*Ltot + 2*K_A_1*K_B_2*Rtot + 2*K_A_1*K_B_3*Ltot + 2*K_A_1*K_B_3*Rtot + 2*K_A_1*Ltot + 2*K_A_1*Rtot + K_B_1^2*K_B_2^2 + 2*K_B_1^2*K_B_2 + K_B_1^2 + 2*K_B_1*K_B_2^2 + 4*K_B_1*K_B_2 + 2*K_B_1 + K_B_2^2 + 2*K_B_2 + 1)^(1/2) + K_B_1*K_B_2 - K_A_1*Ltot + K_A_1*Rtot - K_A_1*K_B_3*Ltot + K_A_1*K_B_3*Rtot + 1)/(K_B_2 + K_B_3 + K_B_2*K_B_3 + 1) < 0 and -(K_B_1 + K_B_2 - (K_A_1^2*K_B_3^2*Ltot^2 - 2*K_A_1^2*K_B_3^2*Ltot*Rtot + K_A_1^2*K_B_3^2*Rtot^2 + 2*K_A_1^2*K_B_3*Ltot^2 - 4*K_A_1^2*K_B_3*Ltot*Rtot + 2*K_A_1^2*K_B_3*Rtot^2 + K_A_1^2*Ltot^2 - 2*K_A_1^2*Ltot*Rtot + K_A_1^2*Rtot^2 + 2*K_A_1*K_B_1*K_B_2*K_B_3*Ltot + 2*K_A_1*K_B_1*K_B_2*K_B_3*Rtot + 2*K_A_1*K_B_1*K_B_2*Ltot + 2*K_A_1*K_B_1*K_B_2*Rtot + 2*K_A_1*K_B_1*K_B_3*Ltot + 2*K_A_1*K_B_1*K_B_3*Rtot + 2*K_A_1*K_B_1*Ltot + 2*K_A_1*K_B_1*Rtot + 2*K_A_1*K_B_2*K_B_3*Ltot + 2*K_A_1*K_B_2*K_B_3*Rtot + 2*K_A_1*K_B_2*Ltot + 2*K_A_1*K_B_2*Rtot + 2*K_A_1*K_B_3*Ltot + 2*K_A_1*K_B_3*Rtot + 2*K_A_1*Ltot + 2*K_A_1*Rtot + K_B_1^2*K_B_2^2 + 2*K_B_1^2*K_B_2 + K_B_1^2 + 2*K_B_1*K_B_2^2 + 4*K_B_1*K_B_2 + 2*K_B_1 + K_B_2^2 + 2*K_B_2 + 1)^(1/2) + K_B_1*K_B_2 - K_A_1*Ltot + K_A_1*Rtot - K_A_1*K_B_3*Ltot + K_A_1*K_B_3*Rtot + 1)/(2*K_A_1*(K_B_2 + K_B_3 + K_B_2*K_B_3 + 1)) < Ltot and (K_B_1 + K_B_2 - (K_A_1^2*K_B_3^2*Ltot^2 - 2*K_A_1^2*K_B_3^2*Ltot*Rtot + K_A_1^2*K_B_3^2*Rtot^2 + 2*K_A_1^2*K_B_3*Ltot^2 - 4*K_A_1^2*K_B_3*Ltot*Rtot + 2*K_A_1^2*K_B_3*Rtot^2 + K_A_1^2*Ltot^2 - 2*K_A_1^2*Ltot*Rtot + K_A_1^2*Rtot^2 + 2*K_A_1*K_B_1*K_B_2*K_B_3*Ltot + 2*K_A_1*K_B_1*K_B_2*K_B_3*Rtot + 2*K_A_1*K_B_1*K_B_2*Ltot + 2*K_A_1*K_B_1*K_B_2*Rtot + 2*K_A_1*K_B_1*K_B_3*Ltot + 2*K_A_1*K_B_1*K_B_3*Rtot + 2*K_A_1*K_B_1*Ltot + 2*K_A_1*K_B_1*Rtot + 2*K_A_1*K_B_2*K_B_3*Ltot + 2*K_A_1*K_B_2*K_B_3*Rtot + 2*K_A_1*K_B_2*Ltot + 2*K_A_1*K_B_2*Rtot + 2*K_A_1*K_B_3*Ltot + 2*K_A_1*K_B_3*Rtot + 2*K_A_1*Ltot + 2*K_A_1*Rtot + K_B_1^2*K_B_2^2 + 2*K_B_1^2*K_B_2 + K_B_1^2 + 2*K_B_1*K_B_2^2 + 4*K_B_1*K_B_2 + 2*K_B_1 + K_B_2^2 + 2*K_B_2 + 1)^(1/2) + K_B_1*K_B_2 - K_A_1*Ltot + K_A_1*Rtot - K_A_1*K_B_3*Ltot + K_A_1*K_B_3*Rtot + 1)/(K_B_2 + K_B_3 + K_B_2*K_B_3 + 1) < 0 and (K_A_1^2*K_B_3^2*Ltot^2 - 2*K_A_1^2*K_B_3^2*Ltot*Rtot + K_A_1^2*K_B_3^2*Rtot^2 + 2*K_A_1^2*K_B_3*Ltot^2 - 4*K_A_1^2*K_B_3*Ltot*Rtot + 2*K_A_1^2*K_B_3*Rtot^2 + K_A_1^2*Ltot^2 - 2*K_A_1^2*Ltot*Rtot + K_A_1^2*Rtot^2 + 2*K_A_1*K_B_1*K_B_2*K_B_3*Ltot + 2*K_A_1*K_B_1*K_B_2*K_B_3*Rtot + 2*K_A_1*K_B_1*K_B_2*Ltot + 2*K_A_1*K_B_1*K_B_2*Rtot + 2*K_A_1*K_B_1*K_B_3*Ltot + 2*K_A_1*K_B_1*K_B_3*Rtot + 2*K_A_1*K_B_1*Ltot + 2*K_A_1*K_B_1*Rtot + 2*K_A_1*K_B_2*K_B_3*Ltot + 2*K_A_1*K_B_2*K_B_3*Rtot + 2*K_A_1*K_B_2*Ltot + 2*K_A_1*K_B_2*Rtot + 2*K_A_1*K_B_3*Ltot + 2*K_A_1*K_B_3*Rtot + 2*K_A_1*Ltot + 2*K_A_1*Rtot + K_B_1^2*K_B_2^2 + 2*K_B_1^2*K_B_2 + K_B_1^2 + 2*K_B_1*K_B_2^2 + 4*K_B_1*K_B_2 + 2*K_B_1 + K_B_2^2 + 2*K_B_2 + 1)^(1/2) + K_A_1*Ltot + K_A_1*K_B_3*Ltot <> K_B_1 + K_B_2 + K_B_1*K_B_2 + K_A_1*Rtot + K_A_1*K_B_3*Rtot + 1 and K_B_1 + K_B_2 + (K_A_1^2*K_B_3^2*Ltot^2 - 2*K_A_1^2*K_B_3^2*Ltot*Rtot + K_A_1^2*K_B_3^2*Rtot^2 + 2*K_A_1^2*K_B_3*Ltot^2 - 4*K_A_1^2*K_B_3*Ltot*Rtot + 2*K_A_1^2*K_B_3*Rtot^2 + K_A_1^2*Ltot^2 - 2*K_A_1^2*Ltot*Rtot + K_A_1^2*Rtot^2 + 2*K_A_1*K_B_1*K_B_2*K_B_3*Ltot + 2*K_A_1*K_B_1*K_B_2*K_B_3*Rtot + 2*K_A_1*K_B_1*K_B_2*Ltot + 2*K_A_1*K_B_1*K_B_2*Rtot + 2*K_A_1*K_B_1*K_B_3*Ltot + 2*K_A_1*K_B_1*K_B_3*Rtot + 2*K_A_1*K_B_1*Ltot + 2*K_A_1*K_B_1*Rtot + 2*K_A_1*K_B_2*K_B_3*Ltot + 2*K_A_1*K_B_2*K_B_3*Rtot + 2*K_A_1*K_B_2*Ltot + 2*K_A_1*K_B_2*Rtot + 2*K_A_1*K_B_3*Ltot + 2*K_A_1*K_B_3*Rtot + 2*K_A_1*Ltot + 2*K_A_1*Rtot + K_B_1^2*K_B_2^2 + 2*K_B_1^2*K_B_2 + K_B_1^2 + 2*K_B_1*K_B_2^2 + 4*K_B_1*K_B_2 + 2*K_B_1 + K_B_2^2 + 2*K_B_2 + 1)^(1/2) + K_B_1*K_B_2 + K_A_1*Rtot + K_A_1*K_B_3*Rtot + 1 <> K_A_1*Ltot + K_A_1*K_B_3*Ltot, {-(K_B_1 + K_B_2 + (K_A_1^2*K_B_3^2*Ltot^2 - 2*K_A_1^2*K_B_3^2*Ltot*Rtot + K_A_1^2*K_B_3^2*Rtot^2 + 2*K_A_1^2*K_B_3*Ltot^2 - 4*K_A_1^2*K_B_3*Ltot*Rtot + 2*K_A_1^2*K_B_3*Rtot^2 + K_A_1^2*Ltot^2 - 2*K_A_1^2*Ltot*Rtot + K_A_1^2*Rtot^2 + 2*K_A_1*K_B_1*K_B_2*K_B_3*Ltot + 2*K_A_1*K_B_1*K_B_2*K_B_3*Rtot + 2*K_A_1*K_B_1*K_B_2*Ltot + 2*K_A_1*K_B_1*K_B_2*Rtot + 2*K_A_1*K_B_1*K_B_3*Ltot + 2*K_A_1*K_B_1*K_B_3*Rtot + 2*K_A_1*K_B_1*Ltot + 2*K_A_1*K_B_1*Rtot + 2*K_A_1*K_B_2*K_B_3*Ltot + 2*K_A_1*K_B_2*K_B_3*Rtot + 2*K_A_1*K_B_2*Ltot + 2*K_A_1*K_B_2*Rtot + 2*K_A_1*K_B_3*Ltot + 2*K_A_1*K_B_3*Rtot + 2*K_A_1*Ltot + 2*K_A_1*Rtot + K_B_1^2*K_B_2^2 + 2*K_B_1^2*K_B_2 + K_B_1^2 + 2*K_B_1*K_B_2^2 + 4*K_B_1*K_B_2 + 2*K_B_1 + K_B_2^2 + 2*K_B_2 + 1)^(1/2) + K_B_1*K_B_2 - K_A_1*Ltot + K_A_1*Rtot - K_A_1*K_B_3*Ltot + K_A_1*K_B_3*Rtot + 1)/(2*(K_A_1 + K_A_1*K_B_2 + K_A_1*K_B_3 + K_A_1*K_B_2*K_B_3)), -(K_B_1 + K_B_2 - (K_A_1^2*K_B_3^2*Ltot^2 - 2*K_A_1^2*K_B_3^2*Ltot*Rtot + K_A_1^2*K_B_3^2*Rtot^2 + 2*K_A_1^2*K_B_3*Ltot^2 - 4*K_A_1^2*K_B_3*Ltot*Rtot + 2*K_A_1^2*K_B_3*Rtot^2 + K_A_1^2*Ltot^2 - 2*K_A_1^2*Ltot*Rtot + K_A_1^2*Rtot^2 + 2*K_A_1*K_B_1*K_B_2*K_B_3*Ltot + 2*K_A_1*K_B_1*K_B_2*K_B_3*Rtot + 2*K_A_1*K_B_1*K_B_2*Ltot + 2*K_A_1*K_B_1*K_B_2*Rtot + 2*K_A_1*K_B_1*K_B_3*Ltot + 2*K_A_1*K_B_1*K_B_3*Rtot + 2*K_A_1*K_B_1*Ltot + 2*K_A_1*K_B_1*Rtot + 2*K_A_1*K_B_2*K_B_3*Ltot + 2*K_A_1*K_B_2*K_B_3*Rtot + 2*K_A_1*K_B_2*Ltot + 2*K_A_1*K_B_2*Rtot + 2*K_A_1*K_B_3*Ltot + 2*K_A_1*K_B_3*Rtot + 2*K_A_1*Ltot + 2*K_A_1*Rtot + K_B_1^2*K_B_2^2 + 2*K_B_1^2*K_B_2 + K_B_1^2 + 2*K_B_1*K_B_2^2 + 4*K_B_1*K_B_2 + 2*K_B_1 + K_B_2^2 + 2*K_B_2 + 1)^(1/2) + K_B_1*K_B_2 - K_A_1*Ltot + K_A_1*Rtot - K_A_1*K_B_3*Ltot + K_A_1*K_B_3*Rtot + 1)/(2*(K_A_1 + K_A_1*K_B_2 + K_A_1*K_B_3 + K_A_1*K_B_2*K_B_3))}], [2*Ltot*Rtot*K_A_1^2*K_B_3^2 + 4*Ltot*Rtot*K_A_1^2*K_B_3 + 2*Ltot*Rtot*K_A_1^2 <= K_A_1^2*K_B_3^2*Ltot^2 + K_A_1^2*K_B_3^2*Rtot^2 + 2*K_A_1^2*K_B_3*Ltot^2 + 2*K_A_1^2*K_B_3*Rtot^2 + K_A_1^2*Ltot^2 + K_A_1^2*Rtot^2 + 2*K_A_1*K_B_1*K_B_2*K_B_3*Ltot + 2*K_A_1*K_B_1*K_B_2*K_B_3*Rtot + 2*K_A_1*K_B_1*K_B_2*Ltot + 2*K_A_1*K_B_1*K_B_2*Rtot + 2*K_A_1*K_B_1*K_B_3*Ltot + 2*K_A_1*K_B_1*K_B_3*Rtot + 2*K_A_1*K_B_1*Ltot + 2*K_A_1*K_B_1*Rtot + 2*K_A_1*K_B_2*K_B_3*Ltot + 2*K_A_1*K_B_2*K_B_3*Rtot + 2*K_A_1*K_B_2*Ltot + 2*K_A_1*K_B_2*Rtot + 2*K_A_1*K_B_3*Ltot + 2*K_A_1*K_B_3*Rtot + 2*K_A_1*Ltot + 2*K_A_1*Rtot + K_B_1^2*K_B_2^2 + 2*K_B_1^2*K_B_2 + K_B_1^2 + 2*K_B_1*K_B_2^2 + 4*K_B_1*K_B_2 + 2*K_B_1 + K_B_2^2 + 2*K_B_2 + 1 and (not -(K_B_1 + K_B_2 - (K_A_1^2*K_B_3^2*Ltot^2 - 2*K_A_1^2*K_B_3^2*Ltot*Rtot + K_A_1^2*K_B_3^2*Rtot^2 + 2*K_A_1^2*K_B_3*Ltot^2 - 4*K_A_1^2*K_B_3*Ltot*Rtot + 2*K_A_1^2*K_B_3*Rtot^2 + K_A_1^2*Ltot^2 - 2*K_A_1^2*Ltot*Rtot + K_A_1^2*Rtot^2 + 2*K_A_1*K_B_1*K_B_2*K_B_3*Ltot + 2*K_A_1*K_B_1*K_B_2*K_B_3*Rtot + 2*K_A_1*K_B_1*K_B_2*Ltot + 2*K_A_1*K_B_1*K_B_2*Rtot + 2*K_A_1*K_B_1*K_B_3*Ltot + 2*K_A_1*K_B_1*K_B_3*Rtot + 2*K_A_1*K_B_1*Ltot + 2*K_A_1*K_B_1*Rtot + 2*K_A_1*K_B_2*K_B_3*Ltot + 2*K_A_1*K_B_2*K_B_3*Rtot + 2*K_A_1*K_B_2*Ltot + 2*K_A_1*K_B_2*Rtot + 2*K_A_1*K_B_3*Ltot + 2*K_A_1*K_B_3*Rtot + 2*K_A_1*Ltot + 2*K_A_1*Rtot + K_B_1^2*K_B_2^2 + 2*K_B_1^2*K_B_2 + K_B_1^2 + 2*K_B_1*K_B_2^2 + 4*K_B_1*K_B_2 + 2*K_B_1 + K_B_2^2 + 2*K_B_2 + 1)^(1/2) + K_B_1*K_B_2 - K_A_1*Ltot + K_A_1*Rtot - K_A_1*K_B_3*Ltot + K_A_1*K_B_3*Rtot + 1)/(2*K_A_1*(K_B_2 + K_B_3 + K_B_2*K_B_3 + 1)) < Ltot or not (K_B_1 + K_B_2 - (K_A_1^2*K_B_3^2*Ltot^2 - 2*K_A_1^2*K_B_3^2*Ltot*Rtot + K_A_1^2*K_B_3^2*Rtot^2 + 2*K_A_1^2*K_B_3*Ltot^2 - 4*K_A_1^2*K_B_3*Ltot*Rtot + 2*K_A_1^2*K_B_3*Rtot^2 + K_A_1^2*Ltot^2 - 2*K_A_1^2*Ltot*Rtot + K_A_1^2*Rtot^2 + 2*K_A_1*K_B_1*K_B_2*K_B_3*Ltot + 2*K_A_1*K_B_1*K_B_2*K_B_3*Rtot + 2*K_A_1*K_B_1*K_B_2*Ltot + 2*K_A_1*K_B_1*K_B_2*Rtot + 2*K_A_1*K_B_1*K_B_3*Ltot + 2*K_A_1*K_B_1*K_B_3*Rtot + 2*K_A_1*K_B_1*Ltot + 2*K_A_1*K_B_1*Rtot + 2*K_A_1*K_B_2*K_B_3*Ltot + 2*K_A_1*K_B_2*K_B_3*Rtot + 2*K_A_1*K_B_2*Ltot + 2*K_A_1*K_B_2*Rtot + 2*K_A_1*K_B_3*Ltot + 2*K_A_1*K_B_3*Rtot + 2*K_A_1*Ltot + 2*K_A_1*Rtot + K_B_1^2*K_B_2^2 + 2*K_B_1^2*K_B_2 + K_B_1^2 + 2*K_B_1*K_B_2^2 + 4*K_B_1*K_B_2 + 2*K_B_1 + K_B_2^2 + 2*K_B_2 + 1)^(1/2) + K_B_1*K_B_2 - K_A_1*Ltot + K_A_1*Rtot - K_A_1*K_B_3*Ltot + K_A_1*K_B_3*Rtot + 1)/(K_B_2 + K_B_3 + K_B_2*K_B_3 + 1) < 0) and -(K_B_1 + K_B_2 + (K_A_1^2*K_B_3^2*Ltot^2 - 2*K_A_1^2*K_B_3^2*Ltot*Rtot + K_A_1^2*K_B_3^2*Rtot^2 + 2*K_A_1^2*K_B_3*Ltot^2 - 4*K_A_1^2*K_B_3*Ltot*Rtot + 2*K_A_1^2*K_B_3*Rtot^2 + K_A_1^2*Ltot^2 - 2*K_A_1^2*Ltot*Rtot + K_A_1^2*Rtot^2 + 2*K_A_1*K_B_1*K_B_2*K_B_3*Ltot + 2*K_A_1*K_B_1*K_B_2*K_B_3*Rtot + 2*K_A_1*K_B_1*K_B_2*Ltot + 2*K_A_1*K_B_1*K_B_2*Rtot + 2*K_A_1*K_B_1*K_B_3*Ltot + 2*K_A_1*K_B_1*K_B_3*Rtot + 2*K_A_1*K_B_1*Ltot + 2*K_A_1*K_B_1*Rtot + 2*K_A_1*K_B_2*K_B_3*Ltot + 2*K_A_1*K_B_2*K_B_3*Rtot + 2*K_A_1*K_B_2*Ltot + 2*K_A_1*K_B_2*Rtot + 2*K_A_1*K_B_3*Ltot + 2*K_A_1*K_B_3*Rtot + 2*K_A_1*Ltot + 2*K_A_1*Rtot + K_B_1^2*K_B_2^2 + 2*K_B_1^2*K_B_2 + K_B_1^2 + 2*K_B_1*K_B_2^2 + 4*K_B_1*K_B_2 + 2*K_B_1 + K_B_2^2 + 2*K_B_2 + 1)^(1/2) + K_B_1*K_B_2 - K_A_1*Ltot + K_A_1*Rtot - K_A_1*K_B_3*Ltot + K_A_1*K_B_3*Rtot + 1)/(2*K_A_1*(K_B_2 + K_B_3 + K_B_2*K_B_3 + 1)) < Ltot and (K_B_1 + K_B_2 + (K_A_1^2*K_B_3^2*Ltot^2 - 2*K_A_1^2*K_B_3^2*Ltot*Rtot + K_A_1^2*K_B_3^2*Rtot^2 + 2*K_A_1^2*K_B_3*Ltot^2 - 4*K_A_1^2*K_B_3*Ltot*Rtot + 2*K_A_1^2*K_B_3*Rtot^2 + K_A_1^2*Ltot^2 - 2*K_A_1^2*Ltot*Rtot + K_A_1^2*Rtot^2 + 2*K_A_1*K_B_1*K_B_2*K_B_3*Ltot + 2*K_A_1*K_B_1*K_B_2*K_B_3*Rtot + 2*K_A_1*K_B_1*K_B_2*Ltot + 2*K_A_1*K_B_1*K_B_2*Rtot + 2*K_A_1*K_B_1*K_B_3*Ltot + 2*K_A_1*K_B_1*K_B_3*Rtot + 2*K_A_1*K_B_1*Ltot + 2*K_A_1*K_B_1*Rtot + 2*K_A_1*K_B_2*K_B_3*Ltot + 2*K_A_1*K_B_2*K_B_3*Rtot + 2*K_A_1*K_B_2*Ltot + 2*K_A_1*K_B_2*Rtot + 2*K_A_1*K_B_3*Ltot + 2*K_A_1*K_B_3*Rtot + 2*K_A_1*Ltot + 2*K_A_1*Rtot + K_B_1^2*K_B_2^2 + 2*K_B_1^2*K_B_2 + K_B_1^2 + 2*K_B_1*K_B_2^2 + 4*K_B_1*K_B_2 + 2*K_B_1 + K_B_2^2 + 2*K_B_2 + 1)^(1/2) + K_B_1*K_B_2 - K_A_1*Ltot + K_A_1*Rtot - K_A_1*K_B_3*Ltot + K_A_1*K_B_3*Rtot + 1)/(K_B_2 + K_B_3 + K_B_2*K_B_3 + 1) < 0 and (K_A_1^2*K_B_3^2*Ltot^2 - 2*K_A_1^2*K_B_3^2*Ltot*Rtot + K_A_1^2*K_B_3^2*Rtot^2 + 2*K_A_1^2*K_B_3*Ltot^2 - 4*K_A_1^2*K_B_3*Ltot*Rtot + 2*K_A_1^2*K_B_3*Rtot^2 + K_A_1^2*Ltot^2 - 2*K_A_1^2*Ltot*Rtot + K_A_1^2*Rtot^2 + 2*K_A_1*K_B_1*K_B_2*K_B_3*Ltot + 2*K_A_1*K_B_1*K_B_2*K_B_3*Rtot + 2*K_A_1*K_B_1*K_B_2*Ltot + 2*K_A_1*K_B_1*K_B_2*Rtot + 2*K_A_1*K_B_1*K_B_3*Ltot + 2*K_A_1*K_B_1*K_B_3*Rtot + 2*K_A_1*K_B_1*Ltot + 2*K_A_1*K_B_1*Rtot + 2*K_A_1*K_B_2*K_B_3*Ltot + 2*K_A_1*K_B_2*K_B_3*Rtot + 2*K_A_1*K_B_2*Ltot + 2*K_A_1*K_B_2*Rtot + 2*K_A_1*K_B_3*Ltot + 2*K_A_1*K_B_3*Rtot + 2*K_A_1*Ltot + 2*K_A_1*Rtot + K_B_1^2*K_B_2^2 + 2*K_B_1^2*K_B_2 + K_B_1^2 + 2*K_B_1*K_B_2^2 + 4*K_B_1*K_B_2 + 2*K_B_1 + K_B_2^2 + 2*K_B_2 + 1)^(1/2) + K_A_1*Ltot + K_A_1*K_B_3*Ltot <> K_B_1 + K_B_2 + K_B_1*K_B_2 + K_A_1*Rtot + K_A_1*K_B_3*Rtot + 1 and K_B_1 + K_B_2 + (K_A_1^2*K_B_3^2*Ltot^2 - 2*K_A_1^2*K_B_3^2*Ltot*Rtot + K_A_1^2*K_B_3^2*Rtot^2 + 2*K_A_1^2*K_B_3*Ltot^2 - 4*K_A_1^2*K_B_3*Ltot*Rtot + 2*K_A_1^2*K_B_3*Rtot^2 + K_A_1^2*Ltot^2 - 2*K_A_1^2*Ltot*Rtot + K_A_1^2*Rtot^2 + 2*K_A_1*K_B_1*K_B_2*K_B_3*Ltot + 2*K_A_1*K_B_1*K_B_2*K_B_3*Rtot + 2*K_A_1*K_B_1*K_B_2*Ltot + 2*K_A_1*K_B_1*K_B_2*Rtot + 2*K_A_1*K_B_1*K_B_3*Ltot + 2*K_A_1*K_B_1*K_B_3*Rtot + 2*K_A_1*K_B_1*Ltot + 2*K_A_1*K_B_1*Rtot + 2*K_A_1*K_B_2*K_B_3*Ltot + 2*K_A_1*K_B_2*K_B_3*Rtot + 2*K_A_1*K_B_2*Ltot + 2*K_A_1*K_B_2*Rtot + 2*K_A_1*K_B_3*Ltot + 2*K_A_1*K_B_3*Rtot + 2*K_A_1*Ltot + 2*K_A_1*Rtot + K_B_1^2*K_B_2^2 + 2*K_B_1^2*K_B_2 + K_B_1^2 + 2*K_B_1*K_B_2^2 + 4*K_B_1*K_B_2 + 2*K_B_1 + K_B_2^2 + 2*K_B_2 + 1)^(1/2) + K_B_1*K_B_2 + K_A_1*Rtot + K_A_1*K_B_3*Rtot + 1 <> K_A_1*Ltot + K_A_1*K_B_3*Ltot, {-(K_B_1 + K_B_2 + (K_A_1^2*K_B_3^2*Ltot^2 - 2*K_A_1^2*K_B_3^2*Ltot*Rtot + K_A_1^2*K_B_3^2*Rtot^2 + 2*K_A_1^2*K_B_3*Ltot^2 - 4*K_A_1^2*K_B_3*Ltot*Rtot + 2*K_A_1^2*K_B_3*Rtot^2 + K_A_1^2*Ltot^2 - 2*K_A_1^2*Ltot*Rtot + K_A_1^2*Rtot^2 + 2*K_A_1*K_B_1*K_B_2*K_B_3*Ltot + 2*K_A_1*K_B_1*K_B_2*K_B_3*Rtot + 2*K_A_1*K_B_1*K_B_2*Ltot + 2*K_A_1*K_B_1*K_B_2*Rtot + 2*K_A_1*K_B_1*K_B_3*Ltot + 2*K_A_1*K_B_1*K_B_3*Rtot + 2*K_A_1*K_B_1*Ltot + 2*K_A_1*K_B_1*Rtot + 2*K_A_1*K_B_2*K_B_3*Ltot + 2*K_A_1*K_B_2*K_B_3*Rtot + 2*K_A_1*K_B_2*Ltot + 2*K_A_1*K_B_2*Rtot + 2*K_A_1*K_B_3*Ltot + 2*K_A_1*K_B_3*Rtot + 2*K_A_1*Ltot + 2*K_A_1*Rtot + K_B_1^2*K_B_2^2 + 2*K_B_1^2*K_B_2 + K_B_1^2 + 2*K_B_1*K_B_2^2 + 4*K_B_1*K_B_2 + 2*K_B_1 + K_B_2^2 + 2*K_B_2 + 1)^(1/2) + K_B_1*K_B_2 - K_A_1*Ltot + K_A_1*Rtot - K_A_1*K_B_3*Ltot + K_A_1*K_B_3*Rtot + 1)/(2*(K_A_1 + K_A_1*K_B_2 + K_A_1*K_B_3 + K_A_1*K_B_2*K_B_3))}], [2*Ltot*Rtot*K_A_1^2*K_B_3^2 + 4*Ltot*Rtot*K_A_1^2*K_B_3 + 2*Ltot*Rtot*K_A_1^2 <= K_A_1^2*K_B_3^2*Ltot^2 + K_A_1^2*K_B_3^2*Rtot^2 + 2*K_A_1^2*K_B_3*Ltot^2 + 2*K_A_1^2*K_B_3*Rtot^2 + K_A_1^2*Ltot^2 + K_A_1^2*Rtot^2 + 2*K_A_1*K_B_1*K_B_2*K_B_3*Ltot + 2*K_A_1*K_B_1*K_B_2*K_B_3*Rtot + 2*K_A_1*K_B_1*K_B_2*Ltot + 2*K_A_1*K_B_1*K_B_2*Rtot + 2*K_A_1*K_B_1*K_B_3*Ltot + 2*K_A_1*K_B_1*K_B_3*Rtot + 2*K_A_1*K_B_1*Ltot + 2*K_A_1*K_B_1*Rtot + 2*K_A_1*K_B_2*K_B_3*Ltot + 2*K_A_1*K_B_2*K_B_3*Rtot + 2*K_A_1*K_B_2*Ltot + 2*K_A_1*K_B_2*Rtot + 2*K_A_1*K_B_3*Ltot + 2*K_A_1*K_B_3*Rtot + 2*K_A_1*Ltot + 2*K_A_1*Rtot + K_B_1^2*K_B_2^2 + 2*K_B_1^2*K_B_2 + K_B_1^2 + 2*K_B_1*K_B_2^2 + 4*K_B_1*K_B_2 + 2*K_B_1 + K_B_2^2 + 2*K_B_2 + 1 and (not -(K_B_1 + K_B_2 + (K_A_1^2*K_B_3^2*Ltot^2 - 2*K_A_1^2*K_B_3^2*Ltot*Rtot + K_A_1^2*K_B_3^2*Rtot^2 + 2*K_A_1^2*K_B_3*Ltot^2 - 4*K_A_1^2*K_B_3*Ltot*Rtot + 2*K_A_1^2*K_B_3*Rtot^2 + K_A_1^2*Ltot^2 - 2*K_A_1^2*Ltot*Rtot + K_A_1^2*Rtot^2 + 2*K_A_1*K_B_1*K_B_2*K_B_3*Ltot + 2*K_A_1*K_B_1*K_B_2*K_B_3*Rtot + 2*K_A_1*K_B_1*K_B_2*Ltot + 2*K_A_1*K_B_1*K_B_2*Rtot + 2*K_A_1*K_B_1*K_B_3*Ltot + 2*K_A_1*K_B_1*K_B_3*Rtot + 2*K_A_1*K_B_1*Ltot + 2*K_A_1*K_B_1*Rtot + 2*K_A_1*K_B_2*K_B_3*Ltot + 2*K_A_1*K_B_2*K_B_3*Rtot + 2*K_A_1*K_B_2*Ltot + 2*K_A_1*K_B_2*Rtot + 2*K_A_1*K_B_3*Ltot + 2*K_A_1*K_B_3*Rtot + 2*K_A_1*Ltot + 2*K_A_1*Rtot + K_B_1^2*K_B_2^2 + 2*K_B_1^2*K_B_2 + K_B_1^2 + 2*K_B_1*K_B_2^2 + 4*K_B_1*K_B_2 + 2*K_B_1 + K_B_2^2 + 2*K_B_2 + 1)^(1/2) + K_B_1*K_B_2 - K_A_1*Ltot + K_A_1*Rtot - K_A_1*K_B_3*Ltot + K_A_1*K_B_3*Rtot + 1)/(2*K_A_1*(K_B_2 + K_B_3 + K_B_2*K_B_3 + 1)) < Ltot or not (K_B_1 + K_B_2 + (K_A_1^2*K_B_3^2*Ltot^2 - 2*K_A_1^2*K_B_3^2*Ltot*Rtot + K_A_1^2*K_B_3^2*Rtot^2 + 2*K_A_1^2*K_B_3*Ltot^2 - 4*K_A_1^2*K_B_3*Ltot*Rtot + 2*K_A_1^2*K_B_3*Rtot^2 + K_A_1^2*Ltot^2 - 2*K_A_1^2*Ltot*Rtot + K_A_1^2*Rtot^2 + 2*K_A_1*K_B_1*K_B_2*K_B_3*Ltot + 2*K_A_1*K_B_1*K_B_2*K_B_3*Rtot + 2*K_A_1*K_B_1*K_B_2*Ltot + 2*K_A_1*K_B_1*K_B_2*Rtot + 2*K_A_1*K_B_1*K_B_3*Ltot + 2*K_A_1*K_B_1*K_B_3*Rtot + 2*K_A_1*K_B_1*Ltot + 2*K_A_1*K_B_1*Rtot + 2*K_A_1*K_B_2*K_B_3*Ltot + 2*K_A_1*K_B_2*K_B_3*Rtot + 2*K_A_1*K_B_2*Ltot + 2*K_A_1*K_B_2*Rtot + 2*K_A_1*K_B_3*Ltot + 2*K_A_1*K_B_3*Rtot + 2*K_A_1*Ltot + 2*K_A_1*Rtot + K_B_1^2*K_B_2^2 + 2*K_B_1^2*K_B_2 + K_B_1^2 + 2*K_B_1*K_B_2^2 + 4*K_B_1*K_B_2 + 2*K_B_1 + K_B_2^2 + 2*K_B_2 + 1)^(1/2) + K_B_1*K_B_2 - K_A_1*Ltot + K_A_1*Rtot - K_A_1*K_B_3*Ltot + K_A_1*K_B_3*Rtot + 1)/(K_B_2 + K_B_3 + K_B_2*K_B_3 + 1) < 0) and -(K_B_1 + K_B_2 - (K_A_1^2*K_B_3^2*Ltot^2 - 2*K_A_1^2*K_B_3^2*Ltot*Rtot + K_A_1^2*K_B_3^2*Rtot^2 + 2*K_A_1^2*K_B_3*Ltot^2 - 4*K_A_1^2*K_B_3*Ltot*Rtot + 2*K_A_1^2*K_B_3*Rtot^2 + K_A_1^2*Ltot^2 - 2*K_A_1^2*Ltot*Rtot + K_A_1^2*Rtot^2 + 2*K_A_1*K_B_1*K_B_2*K_B_3*Ltot + 2*K_A_1*K_B_1*K_B_2*K_B_3*Rtot + 2*K_A_1*K_B_1*K_B_2*Ltot + 2*K_A_1*K_B_1*K_B_2*Rtot + 2*K_A_1*K_B_1*K_B_3*Ltot + 2*K_A_1*K_B_1*K_B_3*Rtot + 2*K_A_1*K_B_1*Ltot + 2*K_A_1*K_B_1*Rtot + 2*K_A_1*K_B_2*K_B_3*Ltot + 2*K_A_1*K_B_2*K_B_3*Rtot + 2*K_A_1*K_B_2*Ltot + 2*K_A_1*K_B_2*Rtot + 2*K_A_1*K_B_3*Ltot + 2*K_A_1*K_B_3*Rtot + 2*K_A_1*Ltot + 2*K_A_1*Rtot + K_B_1^2*K_B_2^2 + 2*K_B_1^2*K_B_2 + K_B_1^2 + 2*K_B_1*K_B_2^2 + 4*K_B_1*K_B_2 + 2*K_B_1 + K_B_2^2 + 2*K_B_2 + 1)^(1/2) + K_B_1*K_B_2 - K_A_1*Ltot + K_A_1*Rtot - K_A_1*K_B_3*Ltot + K_A_1*K_B_3*Rtot + 1)/(2*K_A_1*(K_B_2 + K_B_3 + K_B_2*K_B_3 + 1)) < Ltot and (K_B_1 + K_B_2 - (K_A_1^2*K_B_3^2*Ltot^2 - 2*K_A_1^2*K_B_3^2*Ltot*Rtot + K_A_1^2*K_B_3^2*Rtot^2 + 2*K_A_1^2*K_B_3*Ltot^2 - 4*K_A_1^2*K_B_3*Ltot*Rtot + 2*K_A_1^2*K_B_3*Rtot^2 + K_A_1^2*Ltot^2 - 2*K_A_1^2*Ltot*Rtot + K_A_1^2*Rtot^2 + 2*K_A_1*K_B_1*K_B_2*K_B_3*Ltot + 2*K_A_1*K_B_1*K_B_2*K_B_3*Rtot + 2*K_A_1*K_B_1*K_B_2*Ltot + 2*K_A_1*K_B_1*K_B_2*Rtot + 2*K_A_1*K_B_1*K_B_3*Ltot + 2*K_A_1*K_B_1*K_B_3*Rtot + 2*K_A_1*K_B_1*Ltot + 2*K_A_1*K_B_1*Rtot + 2*K_A_1*K_B_2*K_B_3*Ltot + 2*K_A_1*K_B_2*K_B_3*Rtot + 2*K_A_1*K_B_2*Ltot + 2*K_A_1*K_B_2*Rtot + 2*K_A_1*K_B_3*Ltot + 2*K_A_1*K_B_3*Rtot + 2*K_A_1*Ltot + 2*K_A_1*Rtot + K_B_1^2*K_B_2^2 + 2*K_B_1^2*K_B_2 + K_B_1^2 + 2*K_B_1*K_B_2^2 + 4*K_B_1*K_B_2 + 2*K_B_1 + K_B_2^2 + 2*K_B_2 + 1)^(1/2) + K_B_1*K_B_2 - K_A_1*Ltot + K_A_1*Rtot - K_A_1*K_B_3*Ltot + K_A_1*K_B_3*Rtot + 1)/(K_B_2 + K_B_3 + K_B_2*K_B_3 + 1) < 0 and (K_A_1^2*K_B_3^2*Ltot^2 - 2*K_A_1^2*K_B_3^2*Ltot*Rtot + K_A_1^2*K_B_3^2*Rtot^2 + 2*K_A_1^2*K_B_3*Ltot^2 - 4*K_A_1^2*K_B_3*Ltot*Rtot + 2*K_A_1^2*K_B_3*Rtot^2 + K_A_1^2*Ltot^2 - 2*K_A_1^2*Ltot*Rtot + K_A_1^2*Rtot^2 + 2*K_A_1*K_B_1*K_B_2*K_B_3*Ltot + 2*K_A_1*K_B_1*K_B_2*K_B_3*Rtot + 2*K_A_1*K_B_1*K_B_2*Ltot + 2*K_A_1*K_B_1*K_B_2*Rtot + 2*K_A_1*K_B_1*K_B_3*Ltot + 2*K_A_1*K_B_1*K_B_3*Rtot + 2*K_A_1*K_B_1*Ltot + 2*K_A_1*K_B_1*Rtot + 2*K_A_1*K_B_2*K_B_3*Ltot + 2*K_A_1*K_B_2*K_B_3*Rtot + 2*K_A_1*K_B_2*Ltot + 2*K_A_1*K_B_2*Rtot + 2*K_A_1*K_B_3*Ltot + 2*K_A_1*K_B_3*Rtot + 2*K_A_1*Ltot + 2*K_A_1*Rtot + K_B_1^2*K_B_2^2 + 2*K_B_1^2*K_B_2 + K_B_1^2 + 2*K_B_1*K_B_2^2 + 4*K_B_1*K_B_2 + 2*K_B_1 + K_B_2^2 + 2*K_B_2 + 1)^(1/2) + K_A_1*Ltot + K_A_1*K_B_3*Ltot <> K_B_1 + K_B_2 + K_B_1*K_B_2 + K_A_1*Rtot + K_A_1*K_B_3*Rtot + 1 and K_B_1 + K_B_2 + (K_A_1^2*K_B_3^2*Ltot^2 - 2*K_A_1^2*K_B_3^2*Ltot*Rtot + K_A_1^2*K_B_3^2*Rtot^2 + 2*K_A_1^2*K_B_3*Ltot^2 - 4*K_A_1^2*K_B_3*Ltot*Rtot + 2*K_A_1^2*K_B_3*Rtot^2 + K_A_1^2*Ltot^2 - 2*K_A_1^2*Ltot*Rtot + K_A_1^2*Rtot^2 + 2*K_A_1*K_B_1*K_B_2*K_B_3*Ltot + 2*K_A_1*K_B_1*K_B_2*K_B_3*Rtot + 2*K_A_1*K_B_1*K_B_2*Ltot + 2*K_A_1*K_B_1*K_B_2*Rtot + 2*K_A_1*K_B_1*K_B_3*Ltot + 2*K_A_1*K_B_1*K_B_3*Rtot + 2*K_A_1*K_B_1*Ltot + 2*K_A_1*K_B_1*Rtot + 2*K_A_1*K_B_2*K_B_3*Ltot + 2*K_A_1*K_B_2*K_B_3*Rtot + 2*K_A_1*K_B_2*Ltot + 2*K_A_1*K_B_2*Rtot + 2*K_A_1*K_B_3*Ltot + 2*K_A_1*K_B_3*Rtot + 2*K_A_1*Ltot + 2*K_A_1*Rtot + K_B_1^2*K_B_2^2 + 2*K_B_1^2*K_B_2 + K_B_1^2 + 2*K_B_1*K_B_2^2 + 4*K_B_1*K_B_2 + 2*K_B_1 + K_B_2^2 + 2*K_B_2 + 1)^(1/2) + K_B_1*K_B_2 + K_A_1*Rtot + K_A_1*K_B_3*Rtot + 1 <> K_A_1*Ltot + K_A_1*K_B_3*Ltot, {-(K_B_1 + K_B_2 - (K_A_1^2*K_B_3^2*Ltot^2 - 2*K_A_1^2*K_B_3^2*Ltot*Rtot + K_A_1^2*K_B_3^2*Rtot^2 + 2*K_A_1^2*K_B_3*Ltot^2 - 4*K_A_1^2*K_B_3*Ltot*Rtot + 2*K_A_1^2*K_B_3*Rtot^2 + K_A_1^2*Ltot^2 - 2*K_A_1^2*Ltot*Rtot + K_A_1^2*Rtot^2 + 2*K_A_1*K_B_1*K_B_2*K_B_3*Ltot + 2*K_A_1*K_B_1*K_B_2*K_B_3*Rtot + 2*K_A_1*K_B_1*K_B_2*Ltot + 2*K_A_1*K_B_1*K_B_2*Rtot + 2*K_A_1*K_B_1*K_B_3*Ltot + 2*K_A_1*K_B_1*K_B_3*Rtot + 2*K_A_1*K_B_1*Ltot + 2*K_A_1*K_B_1*Rtot + 2*K_A_1*K_B_2*K_B_3*Ltot + 2*K_A_1*K_B_2*K_B_3*Rtot + 2*K_A_1*K_B_2*Ltot + 2*K_A_1*K_B_2*Rtot + 2*K_A_1*K_B_3*Ltot + 2*K_A_1*K_B_3*Rtot + 2*K_A_1*Ltot + 2*K_A_1*Rtot + K_B_1^2*K_B_2^2 + 2*K_B_1^2*K_B_2 + K_B_1^2 + 2*K_B_1*K_B_2^2 + 4*K_B_1*K_B_2 + 2*K_B_1 + K_B_2^2 + 2*K_B_2 + 1)^(1/2) + K_B_1*K_B_2 - K_A_1*Ltot + K_A_1*Rtot - K_A_1*K_B_3*Ltot + K_A_1*K_B_3*Rtot + 1)/(2*(K_A_1 + K_A_1*K_B_2 + K_A_1*K_B_3 + K_A_1*K_B_2*K_B_3))}], [(K_B_1 + K_B_2 + (K_A_1^2*K_B_3^2*Ltot^2 - 2*K_A_1^2*K_B_3^2*Ltot*Rtot + K_A_1^2*K_B_3^2*Rtot^2 + 2*K_A_1^2*K_B_3*Ltot^2 - 4*K_A_1^2*K_B_3*Ltot*Rtot + 2*K_A_1^2*K_B_3*Rtot^2 + K_A_1^2*Ltot^2 - 2*K_A_1^2*Ltot*Rtot + K_A_1^2*Rtot^2 + 2*K_A_1*K_B_1*K_B_2*K_B_3*Ltot + 2*K_A_1*K_B_1*K_B_2*K_B_3*Rtot + 2*K_A_1*K_B_1*K_B_2*Ltot + 2*K_A_1*K_B_1*K_B_2*Rtot + 2*K_A_1*K_B_1*K_B_3*Ltot + 2*K_A_1*K_B_1*K_B_3*Rtot + 2*K_A_1*K_B_1*Ltot + 2*K_A_1*K_B_1*Rtot + 2*K_A_1*K_B_2*K_B_3*Ltot + 2*K_A_1*K_B_2*K_B_3*Rtot + 2*K_A_1*K_B_2*Ltot + 2*K_A_1*K_B_2*Rtot + 2*K_A_1*K_B_3*Ltot + 2*K_A_1*K_B_3*Rtot + 2*K_A_1*Ltot + 2*K_A_1*Rtot + K_B_1^2*K_B_2^2 + 2*K_B_1^2*K_B_2 + K_B_1^2 + 2*K_B_1*K_B_2^2 + 4*K_B_1*K_B_2 + 2*K_B_1 + K_B_2^2 + 2*K_B_2 + 1)^(1/2) + K_B_1*K_B_2 + K_A_1*Rtot + K_A_1*K_B_3*Rtot + 1 = K_A_1*Ltot + K_A_1*K_B_3*Ltot or not (K_B_1 + K_B_2 + (K_A_1^2*K_B_3^2*Ltot^2 - 2*K_A_1^2*K_B_3^2*Ltot*Rtot + K_A_1^2*K_B_3^2*Rtot^2 + 2*K_A_1^2*K_B_3*Ltot^2 - 4*K_A_1^2*K_B_3*Ltot*Rtot + 2*K_A_1^2*K_B_3*Rtot^2 + K_A_1^2*Ltot^2 - 2*K_A_1^2*Ltot*Rtot + K_A_1^2*Rtot^2 + 2*K_A_1*K_B_1*K_B_2*K_B_3*Rtot + 2*K_A_1*K_B_1*K_B_2*Rtot + 2*K_A_1*K_B_1*K_B_3*Rtot + 2*K_A_1*K_B_1*Rtot + 2*K_A_1*K_B_2*K_B_3*Rtot + 2*K_A_1*K_B_2*Rtot + 2*K_A_1*K_B_3*Rtot + 2*K_A_1*Rtot + K_B_1^2*K_B_2^2 + 2*K_B_1^2*K_B_2 + K_B_1^2 + 2*K_B_1*K_B_2^2 + 4*K_B_1*K_B_2 + 2*K_B_1 + K_B_2^2 + 2*K_B_2 + 1)^(1/2) + K_B_1*K_B_2 - K_A_1*Ltot + K_A_1*Rtot - K_A_1*K_B_3*Ltot + K_A_1*K_B_3*Rtot + 1)/(K_B_2 + K_B_3 + K_B_2*K_B_3 + 1) < 0) and (K_A_1^2*K_B_3^2*Ltot^2 - 2*K_A_1^2*K_B_3^2*Ltot*Rtot + K_A_1^2*K_B_3^2*Rtot^2 + 2*K_A_1^2*K_B_3*Ltot^2 - 4*K_A_1^2*K_B_3*Ltot*Rtot + 2*K_A_1^2*K_B_3*Rtot^2 + K_A_1^2*Ltot^2 - 2*K_A_1^2*Ltot*Rtot + K_A_1^2*Rtot^2 + 2*K_A_1*K_B_1*K_B_2*K_B_3*Ltot + 2*K_A_1*K_B_1*K_B_2*K_B_3*Rtot + 2*K_A_1*K_B_1*K_B_2*Ltot + 2*K_A_1*K_B_1*K_B_2*Rtot + 2*K_A_1*K_B_1*K_B_3*Ltot + 2*K_A_1*K_B_1*K_B_3*Rtot + 2*K_A_1*K_B_1*Ltot + 2*K_A_1*K_B_1*Rtot + 2*K_A_1*K_B_2*K_B_3*Ltot + 2*K_A_1*K_B_2*K_B_3*Rtot + 2*K_A_1*K_B_2*Ltot + 2*K_A_1*K_B_2*Rtot + 2*K_A_1*K_B_3*Ltot + 2*K_A_1*K_B_3*Rtot + 2*K_A_1*Ltot + 2*K_A_1*Rtot + K_B_1^2*K_B_2^2 + 2*K_B_1^2*K_B_2 + K_B_1^2 + 2*K_B_1*K_B_2^2 + 4*K_B_1*K_B_2 + 2*K_B_1 + K_B_2^2 + 2*K_B_2 + 1)^(1/2) + K_A_1*Ltot + K_A_1*K_B_3*Ltot = K_B_1 + K_B_2 + K_B_1*K_B_2 + K_A_1*Rtot + K_A_1*K_B_3*Rtot + 1 or (-(K_B_1 + K_B_2 - (K_A_1^2*K_B_3^2*Ltot^2 - 2*K_A_1^2*K_B_3^2*Ltot*Rtot + K_A_1^2*K_B_3^2*Rtot^2 + 2*K_A_1^2*K_B_3*Ltot^2 - 4*K_A_1^2*K_B_3*Ltot*Rtot + 2*K_A_1^2*K_B_3*Rtot^2 + K_A_1^2*Ltot^2 - 2*K_A_1^2*Ltot*Rtot + K_A_1^2*Rtot^2 + 2*K_A_1*K_B_1*K_B_2*K_B_3*Rtot + 2*K_A_1*K_B_1*K_B_2*Rtot + 2*K_A_1*K_B_1*K_B_3*Rtot + 2*K_A_1*K_B_1*Rtot + 2*K_A_1*K_B_2*K_B_3*Rtot + 2*K_A_1*K_B_2*Rtot + 2*K_A_1*K_B_3*Rtot + 2*K_A_1*Rtot + K_B_1^2*K_B_2^2 + 2*K_B_1^2*K_B_2 + K_B_1^2 + 2*K_B_1*K_B_2^2 + 4*K_B_1*K_B_2 + 2*K_B_1 + K_B_2^2 + 2*K_B_2 + 1)^(1/2) + K_B_1*K_B_2 - K_A_1*Ltot + K_A_1*Rtot - K_A_1*K_B_3*Ltot + K_A_1*K_B_3*Rtot + 1)/(2*K_A_1*(K_B_2 + K_B_3 + K_B_2*K_B_3 + 1)) < Ltot and (K_B_1 + K_B_2 - (K_A_1^2*K_B_3^2*Ltot^2 - 2*K_A_1^2*K_B_3^2*Ltot*Rtot + K_A_1^2*K_B_3^2*Rtot^2 + 2*K_A_1^2*K_B_3*Ltot^2 - 4*K_A_1^2*K_B_3*Ltot*Rtot + 2*K_A_1^2*K_B_3*Rtot^2 + K_A_1^2*Ltot^2 - 2*K_A_1^2*Ltot*Rtot + K_A_1^2*Rtot^2 + 2*K_A_1*K_B_1*K_B_2*K_B_3*Rtot + 2*K_A_1*K_B_1*K_B_2*Rtot + 2*K_A_1*K_B_1*K_B_3*Rtot + 2*K_A_1*K_B_1*Rtot + 2*K_A_1*K_B_2*K_B_3*Rtot + 2*K_A_1*K_B_2*Rtot + 2*K_A_1*K_B_3*Rtot + 2*K_A_1*Rtot + K_B_1^2*K_B_2^2 + 2*K_B_1^2*K_B_2 + K_B_1^2 + 2*K_B_1*K_B_2^2 + 4*K_B_1*K_B_2 + 2*K_B_1 + K_B_2^2 + 2*K_B_2 + 1)^(1/2) + K_B_1*K_B_2 - K_A_1*Ltot + K_A_1*Rtot - K_A_1*K_B_3*Ltot + K_A_1*K_B_3*Rtot + 1)/(K_B_2 + K_B_3 + K_B_2*K_B_3 + 1) < 0 and K_B_1 + K_B_2 + (K_A_1^2*K_B_3^2*Ltot^2 - 2*K_A_1^2*K_B_3^2*Ltot*Rtot + K_A_1^2*K_B_3^2*Rtot^2 + 2*K_A_1^2*K_B_3*Ltot^2 - 4*K_A_1^2*K_B_3*Ltot*Rtot + 2*K_A_1^2*K_B_3*Rtot^2 + K_A_1^2*Ltot^2 - 2*K_A_1^2*Ltot*Rtot + K_A_1^2*Rtot^2 + 2*K_A_1*K_B_1*K_B_2*K_B_3*Ltot + 2*K_A_1*K_B_1*K_B_2*K_B_3*Rtot + 2*K_A_1*K_B_1*K_B_2*Ltot + 2*K_A_1*K_B_1*K_B_2*Rtot + 2*K_A_1*K_B_1*K_B_3*Ltot + 2*K_A_1*K_B_1*K_B_3*Rtot + 2*K_A_1*K_B_1*Ltot + 2*K_A_1*K_B_1*Rtot + 2*K_A_1*K_B_2*K_B_3*Ltot + 2*K_A_1*K_B_2*K_B_3*Rtot + 2*K_A_1*K_B_2*Ltot + 2*K_A_1*K_B_2*Rtot + 2*K_A_1*K_B_3*Ltot + 2*K_A_1*K_B_3*Rtot + 2*K_A_1*Ltot + 2*K_A_1*Rtot + K_B_1^2*K_B_2^2 + 2*K_B_1^2*K_B_2 + K_B_1^2 + 2*K_B_1*K_B_2^2 + 4*K_B_1*K_B_2 + 2*K_B_1 + K_B_2^2 + 2*K_B_2 + 1)^(1/2) + K_B_1*K_B_2 + K_A_1*Rtot + K_A_1*K_B_3*Rtot + 1 = K_A_1*Ltot + K_A_1*K_B_3*Ltot and (K_A_1^2*K_B_3^2*Ltot^2 - 2*K_A_1^2*K_B_3^2*Ltot*Rtot + K_A_1^2*K_B_3^2*Rtot^2 + 2*K_A_1^2*K_B_3*Ltot^2 - 4*K_A_1^2*K_B_3*Ltot*Rtot + 2*K_A_1^2*K_B_3*Rtot^2 + K_A_1^2*Ltot^2 - 2*K_A_1^2*Ltot*Rtot + K_A_1^2*Rtot^2 + 2*K_A_1*K_B_1*K_B_2*K_B_3*Ltot + 2*K_A_1*K_B_1*K_B_2*K_B_3*Rtot + 2*K_A_1*K_B_1*K_B_2*Ltot + 2*K_A_1*K_B_1*K_B_2*Rtot + 2*K_A_1*K_B_1*K_B_3*Ltot + 2*K_A_1*K_B_1*K_B_3*Rtot + 2*K_A_1*K_B_1*Ltot + 2*K_A_1*K_B_1*Rtot + 2*K_A_1*K_B_2*K_B_3*Ltot + 2*K_A_1*K_B_2*K_B_3*Rtot + 2*K_A_1*K_B_2*Ltot + 2*K_A_1*K_B_2*Rtot + 2*K_A_1*K_B_3*Ltot + 2*K_A_1*K_B_3*Rtot + 2*K_A_1*Ltot + 2*K_A_1*Rtot + K_B_1^2*K_B_2^2 + 2*K_B_1^2*K_B_2 + K_B_1^2 + 2*K_B_1*K_B_2^2 + 4*K_B_1*K_B_2 + 2*K_B_1 + K_B_2^2 + 2*K_B_2 + 1)^(1/2) + K_A_1*Ltot + K_A_1*K_B_3*Ltot <> K_B_1 + K_B_2 + K_B_1*K_B_2 + K_A_1*Rtot + K_A_1*K_B_3*Rtot + 1 or (K_A_1^2*K_B_3^2*Ltot^2 - 2*K_A_1^2*K_B_3^2*Ltot*Rtot + K_A_1^2*K_B_3^2*Rtot^2 + 2*K_A_1^2*K_B_3*Ltot^2 - 4*K_A_1^2*K_B_3*Ltot*Rtot + 2*K_A_1^2*K_B_3*Rtot^2 + K_A_1^2*Ltot^2 - 2*K_A_1^2*Ltot*Rtot + K_A_1^2*Rtot^2 + 2*K_A_1*K_B_1*K_B_2*K_B_3*Ltot + 2*K_A_1*K_B_1*K_B_2*K_B_3*Rtot + 2*K_A_1*K_B_1*K_B_2*Ltot + 2*K_A_1*K_B_1*K_B_2*Rtot + 2*K_A_1*K_B_1*K_B_3*Ltot + 2*K_A_1*K_B_1*K_B_3*Rtot + 2*K_A_1*K_B_1*Ltot + 2*K_A_1*K_B_1*Rtot + 2*K_A_1*K_B_2*K_B_3*Ltot + 2*K_A_1*K_B_2*K_B_3*Rtot + 2*K_A_1*K_B_2*Ltot + 2*K_A_1*K_B_2*Rtot + 2*K_A_1*K_B_3*Ltot + 2*K_A_1*K_B_3*Rtot + 2*K_A_1*Ltot + 2*K_A_1*Rtot + K_B_1^2*K_B_2^2 + 2*K_B_1^2*K_B_2 + K_B_1^2 + 2*K_B_1*K_B_2^2 + 4*K_B_1*K_B_2 + 2*K_B_1 + K_B_2^2 + 2*K_B_2 + 1)^(1/2) + K_A_1*Ltot + K_A_1*K_B_3*Ltot = K_B_1 + K_B_2 + K_B_1*K_B_2 + K_A_1*Rtot + K_A_1*K_B_3*Rtot + 1 and K_B_1 + K_B_2 + (K_A_1^2*K_B_3^2*Ltot^2 - 2*K_A_1^2*K_B_3^2*Ltot*Rtot + K_A_1^2*K_B_3^2*Rtot^2 + 2*K_A_1^2*K_B_3*Ltot^2 - 4*K_A_1^2*K_B_3*Ltot*Rtot + 2*K_A_1^2*K_B_3*Rtot^2 + K_A_1^2*Ltot^2 - 2*K_A_1^2*Ltot*Rtot + K_A_1^2*Rtot^2 + 2*K_A_1*K_B_1*K_B_2*K_B_3*Ltot + 2*K_A_1*K_B_1*K_B_2*K_B_3*Rtot + 2*K_A_1*K_B_1*K_B_2*Ltot + 2*K_A_1*K_B_1*K_B_2*Rtot + 2*K_A_1*K_B_1*K_B_3*Ltot + 2*K_A_1*K_B_1*K_B_3*Rtot + 2*K_A_1*K_B_1*Ltot + 2*K_A_1*K_B_1*Rtot + 2*K_A_1*K_B_2*K_B_3*Ltot + 2*K_A_1*K_B_2*K_B_3*Rtot + 2*K_A_1*K_B_2*Ltot + 2*K_A_1*K_B_2*Rtot + 2*K_A_1*K_B_3*Ltot + 2*K_A_1*K_B_3*Rtot + 2*K_A_1*Ltot + 2*K_A_1*Rtot + K_B_1^2*K_B_2^2 + 2*K_B_1^2*K_B_2 + K_B_1^2 + 2*K_B_1*K_B_2^2 + 4*K_B_1*K_B_2 + 2*K_B_1 + K_B_2^2 + 2*K_B_2 + 1)^(1/2) + K_B_1*K_B_2 + K_A_1*Rtot + K_A_1*K_B_3*Rtot + 1 <> K_A_1*Ltot + K_A_1*K_B_3*Ltot and -(K_B_1 + K_B_2 + (K_A_1^2*K_B_3^2*Ltot^2 - 2*K_A_1^2*K_B_3^2*Ltot*Rtot + K_A_1^2*K_B_3^2*Rtot^2 + 2*K_A_1^2*K_B_3*Ltot^2 - 4*K_A_1^2*K_B_3*Ltot*Rtot + 2*K_A_1^2*K_B_3*Rtot^2 + K_A_1^2*Ltot^2 - 2*K_A_1^2*Ltot*Rtot + K_A_1^2*Rtot^2 + 2*K_A_1*K_B_1*K_B_2*K_B_3*Rtot + 2*K_A_1*K_B_1*K_B_2*Rtot + 2*K_A_1*K_B_1*K_B_3*Rtot + 2*K_A_1*K_B_1*Rtot + 2*K_A_1*K_B_2*K_B_3*Rtot + 2*K_A_1*K_B_2*Rtot + 2*K_A_1*K_B_3*Rtot + 2*K_A_1*Rtot + K_B_1^2*K_B_2^2 + 2*K_B_1^2*K_B_2 + K_B_1^2 + 2*K_B_1*K_B_2^2 + 4*K_B_1*K_B_2 + 2*K_B_1 + K_B_2^2 + 2*K_B_2 + 1)^(1/2) + K_B_1*K_B_2 - K_A_1*Ltot + K_A_1*Rtot - K_A_1*K_B_3*Ltot + K_A_1*K_B_3*Rtot + 1)/(2*K_A_1*(K_B_2 + K_B_3 + K_B_2*K_B_3 + 1)) < Ltot and (K_B_1 + K_B_2 + (K_A_1^2*K_B_3^2*Ltot^2 - 2*K_A_1^2*K_B_3^2*Ltot*Rtot + K_A_1^2*K_B_3^2*Rtot^2 + 2*K_A_1^2*K_B_3*Ltot^2 - 4*K_A_1^2*K_B_3*Ltot*Rtot + 2*K_A_1^2*K_B_3*Rtot^2 + K_A_1^2*Ltot^2 - 2*K_A_1^2*Ltot*Rtot + K_A_1^2*Rtot^2 + 2*K_A_1*K_B_1*K_B_2*K_B_3*Rtot + 2*K_A_1*K_B_1*K_B_2*Rtot + 2*K_A_1*K_B_1*K_B_3*Rtot + 2*K_A_1*K_B_1*Rtot + 2*K_A_1*K_B_2*K_B_3*Rtot + 2*K_A_1*K_B_2*Rtot + 2*K_A_1*K_B_3*Rtot + 2*K_A_1*Rtot + K_B_1^2*K_B_2^2 + 2*K_B_1^2*K_B_2 + K_B_1^2 + 2*K_B_1*K_B_2^2 + 4*K_B_1*K_B_2 + 2*K_B_1 + K_B_2^2 + 2*K_B_2 + 1)^(1/2) + K_B_1*K_B_2 - K_A_1*Ltot + K_A_1*Rtot - K_A_1*K_B_3*Ltot + K_A_1*K_B_3*Rtot + 1)/(K_B_2 + K_B_3 + K_B_2*K_B_3 + 1) < 0) and K_A_1^2*K_B_3^2*Ltot^2 + K_A_1^2*K_B_3^2*Rtot^2 + 2*K_A_1^2*K_B_3*Ltot^2 + 2*K_A_1^2*K_B_3*Rtot^2 + K_A_1^2*Ltot^2 + K_A_1^2*Rtot^2 + 2*K_A_1*K_B_1*K_B_2*K_B_3*Rtot + 2*K_A_1*K_B_1*K_B_2*Rtot + 2*K_A_1*K_B_1*K_B_3*Rtot + 2*K_A_1*K_B_1*Rtot + 2*K_A_1*K_B_2*K_B_3*Rtot + 2*K_A_1*K_B_2*Rtot + 2*K_A_1*K_B_3*Rtot + 2*K_A_1*Rtot + K_B_1^2*K_B_2^2 + 2*K_B_1^2*K_B_2 + K_B_1^2 + 2*K_B_1*K_B_2^2 + 4*K_B_1*K_B_2 + 2*K_B_1 + K_B_2^2 + 2*K_B_2 + 1 < 2*Ltot*Rtot*K_A_1^2*K_B_3^2 + 4*Ltot*Rtot*K_A_1^2*K_B_3 + 2*Ltot*Rtot*K_A_1^2 or not (K_B_1 + K_B_2 - (K_A_1^2*K_B_3^2*Ltot^2 - 2*K_A_1^2*K_B_3^2*Ltot*Rtot + K_A_1^2*K_B_3^2*Rtot^2 + 2*K_A_1^2*K_B_3*Ltot^2 - 4*K_A_1^2*K_B_3*Ltot*Rtot + 2*K_A_1^2*K_B_3*Rtot^2 + K_A_1^2*Ltot^2 - 2*K_A_1^2*Ltot*Rtot + K_A_1^2*Rtot^2 + 2*K_A_1*K_B_1*K_B_2*K_B_3*Rtot + 2*K_A_1*K_B_1*K_B_2*Rtot + 2*K_A_1*K_B_1*K_B_3*Rtot + 2*K_A_1*K_B_1*Rtot + 2*K_A_1*K_B_2*K_B_3*Rtot + 2*K_A_1*K_B_2*Rtot + 2*K_A_1*K_B_3*Rtot + 2*K_A_1*Rtot + K_B_1^2*K_B_2^2 + 2*K_B_1^2*K_B_2 + K_B_1^2 + 2*K_B_1*K_B_2^2 + 4*K_B_1*K_B_2 + 2*K_B_1 + K_B_2^2 + 2*K_B_2 + 1)^(1/2) + K_B_1*K_B_2 - K_A_1*Ltot + K_A_1*Rtot - K_A_1*K_B_3*Ltot + K_A_1*K_B_3*Rtot + 1)/(K_B_2 + K_B_3 + K_B_2*K_B_3 + 1) < 0 and K_B_1 + K_B_2 + (K_A_1^2*K_B_3^2*Ltot^2 - 2*K_A_1^2*K_B_3^2*Ltot*Rtot + K_A_1^2*K_B_3^2*Rtot^2 + 2*K_A_1^2*K_B_3*Ltot^2 - 4*K_A_1^2*K_B_3*Ltot*Rtot + 2*K_A_1^2*K_B_3*Rtot^2 + K_A_1^2*Ltot^2 - 2*K_A_1^2*Ltot*Rtot + K_A_1^2*Rtot^2 + 2*K_A_1*K_B_1*K_B_2*K_B_3*Ltot + 2*K_A_1*K_B_1*K_B_2*K_B_3*Rtot + 2*K_A_1*K_B_1*K_B_2*Ltot + 2*K_A_1*K_B_1*K_B_2*Rtot + 2*K_A_1*K_B_1*K_B_3*Ltot + 2*K_A_1*K_B_1*K_B_3*Rtot + 2*K_A_1*K_B_1*Ltot + 2*K_A_1*K_B_1*Rtot + 2*K_A_1*K_B_2*K_B_3*Ltot + 2*K_A_1*K_B_2*K_B_3*Rtot + 2*K_A_1*K_B_2*Ltot + 2*K_A_1*K_B_2*Rtot + 2*K_A_1*K_B_3*Ltot + 2*K_A_1*K_B_3*Rtot + 2*K_A_1*Ltot + 2*K_A_1*Rtot + K_B_1^2*K_B_2^2 + 2*K_B_1^2*K_B_2 + K_B_1^2 + 2*K_B_1*K_B_2^2 + 4*K_B_1*K_B_2 + 2*K_B_1 + K_B_2^2 + 2*K_B_2 + 1)^(1/2) + K_B_1*K_B_2 + K_A_1*Rtot + K_A_1*K_B_3*Rtot + 1 = K_A_1*Ltot + K_A_1*K_B_3*Ltot and (K_A_1^2*K_B_3^2*Ltot^2 - 2*K_A_1^2*K_B_3^2*Ltot*Rtot + K_A_1^2*K_B_3^2*Rtot^2 + 2*K_A_1^2*K_B_3*Ltot^2 - 4*K_A_1^2*K_B_3*Ltot*Rtot + 2*K_A_1^2*K_B_3*Rtot^2 + K_A_1^2*Ltot^2 - 2*K_A_1^2*Ltot*Rtot + K_A_1^2*Rtot^2 + 2*K_A_1*K_B_1*K_B_2*K_B_3*Ltot + 2*K_A_1*K_B_1*K_B_2*K_B_3*Rtot + 2*K_A_1*K_B_1*K_B_2*Ltot + 2*K_A_1*K_B_1*K_B_2*Rtot + 2*K_A_1*K_B_1*K_B_3*Ltot + 2*K_A_1*K_B_1*K_B_3*Rtot + 2*K_A_1*K_B_1*Ltot + 2*K_A_1*K_B_1*Rtot + 2*K_A_1*K_B_2*K_B_3*Ltot + 2*K_A_1*K_B_2*K_B_3*Rtot + 2*K_A_1*K_B_2*Ltot + 2*K_A_1*K_B_2*Rtot + 2*K_A_1*K_B_3*Ltot + 2*K_A_1*K_B_3*Rtot + 2*K_A_1*Ltot + 2*K_A_1*Rtot + K_B_1^2*K_B_2^2 + 2*K_B_1^2*K_B_2 + K_B_1^2 + 2*K_B_1*K_B_2^2 + 4*K_B_1*K_B_2 + 2*K_B_1 + K_B_2^2 + 2*K_B_2 + 1)^(1/2) + K_A_1*Ltot + K_A_1*K_B_3*Ltot <> K_B_1 + K_B_2 + K_B_1*K_B_2 + K_A_1*Rtot + K_A_1*K_B_3*Rtot + 1 or (K_A_1^2*K_B_3^2*Ltot^2 - 2*K_A_1^2*K_B_3^2*Ltot*Rtot + K_A_1^2*K_B_3^2*Rtot^2 + 2*K_A_1^2*K_B_3*Ltot^2 - 4*K_A_1^2*K_B_3*Ltot*Rtot + 2*K_A_1^2*K_B_3*Rtot^2 + K_A_1^2*Ltot^2 - 2*K_A_1^2*Ltot*Rtot + K_A_1^2*Rtot^2 + 2*K_A_1*K_B_1*K_B_2*K_B_3*Ltot + 2*K_A_1*K_B_1*K_B_2*K_B_3*Rtot + 2*K_A_1*K_B_1*K_B_2*Ltot + 2*K_A_1*K_B_1*K_B_2*Rtot + 2*K_A_1*K_B_1*K_B_3*Ltot + 2*K_A_1*K_B_1*K_B_3*Rtot + 2*K_A_1*K_B_1*Ltot + 2*K_A_1*K_B_1*Rtot + 2*K_A_1*K_B_2*K_B_3*Ltot + 2*K_A_1*K_B_2*K_B_3*Rtot + 2*K_A_1*K_B_2*Ltot + 2*K_A_1*K_B_2*Rtot + 2*K_A_1*K_B_3*Ltot + 2*K_A_1*K_B_3*Rtot + 2*K_A_1*Ltot + 2*K_A_1*Rtot + K_B_1^2*K_B_2^2 + 2*K_B_1^2*K_B_2 + K_B_1^2 + 2*K_B_1*K_B_2^2 + 4*K_B_1*K_B_2 + 2*K_B_1 + K_B_2^2 + 2*K_B_2 + 1)^(1/2) + K_A_1*Ltot + K_A_1*K_B_3*Ltot = K_B_1 + K_B_2 + K_B_1*K_B_2 + K_A_1*Rtot + K_A_1*K_B_3*Rtot + 1 and K_B_1 + K_B_2 + (K_A_1^2*K_B_3^2*Ltot^2 - 2*K_A_1^2*K_B_3^2*Ltot*Rtot + K_A_1^2*K_B_3^2*Rtot^2 + 2*K_A_1^2*K_B_3*Ltot^2 - 4*K_A_1^2*K_B_3*Ltot*Rtot + 2*K_A_1^2*K_B_3*Rtot^2 + K_A_1^2*Ltot^2 - 2*K_A_1^2*Ltot*Rtot + K_A_1^2*Rtot^2 + 2*K_A_1*K_B_1*K_B_2*K_B_3*Ltot + 2*K_A_1*K_B_1*K_B_2*K_B_3*Rtot + 2*K_A_1*K_B_1*K_B_2*Ltot + 2*K_A_1*K_B_1*K_B_2*Rtot + 2*K_A_1*K_B_1*K_B_3*Ltot + 2*K_A_1*K_B_1*K_B_3*Rtot + 2*K_A_1*K_B_1*Ltot + 2*K_A_1*K_B_1*Rtot + 2*K_A_1*K_B_2*K_B_3*Ltot + 2*K_A_1*K_B_2*K_B_3*Rtot + 2*K_A_1*K_B_2*Ltot + 2*K_A_1*K_B_2*Rtot + 2*K_A_1*K_B_3*Ltot + 2*K_A_1*K_B_3*Rtot + 2*K_A_1*Ltot + 2*K_A_1*Rtot + K_B_1^2*K_B_2^2 + 2*K_B_1^2*K_B_2 + K_B_1^2 + 2*K_B_1*K_B_2^2 + 4*K_B_1*K_B_2 + 2*K_B_1 + K_B_2^2 + 2*K_B_2 + 1)^(1/2) + K_B_1*K_B_2 + K_A_1*Rtot + K_A_1*K_B_3*Rtot + 1 <> K_A_1*Ltot + K_A_1*K_B_3*Ltot and not -(K_B_1 + K_B_2 + (K_A_1^2*K_B_3^2*Ltot^2 - 2*K_A_1^2*K_B_3^2*Ltot*Rtot + K_A_1^2*K_B_3^2*Rtot^2 + 2*K_A_1^2*K_B_3*Ltot^2 - 4*K_A_1^2*K_B_3*Ltot*Rtot + 2*K_A_1^2*K_B_3*Rtot^2 + K_A_1^2*Ltot^2 - 2*K_A_1^2*Ltot*Rtot + K_A_1^2*Rtot^2 + 2*K_A_1*K_B_1*K_B_2*K_B_3*Rtot + 2*K_A_1*K_B_1*K_B_2*Rtot + 2*K_A_1*K_B_1*K_B_3*Rtot + 2*K_A_1*K_B_1*Rtot + 2*K_A_1*K_B_2*K_B_3*Rtot + 2*K_A_1*K_B_2*Rtot + 2*K_A_1*K_B_3*Rtot + 2*K_A_1*Rtot + K_B_1^2*K_B_2^2 + 2*K_B_1^2*K_B_2 + K_B_1^2 + 2*K_B_1*K_B_2^2 + 4*K_B_1*K_B_2 + 2*K_B_1 + K_B_2^2 + 2*K_B_2 + 1)^(1/2) + K_B_1*K_B_2 - K_A_1*Ltot + K_A_1*Rtot - K_A_1*K_B_3*Ltot + K_A_1*K_B_3*Rtot + 1)/(2*K_A_1*(K_B_2 + K_B_3 + K_B_2*K_B_3 + 1)) < Ltot and (K_B_1 + K_B_2 + (K_A_1^2*K_B_3^2*Ltot^2 - 2*K_A_1^2*K_B_3^2*Ltot*Rtot + K_A_1^2*K_B_3^2*Rtot^2 + 2*K_A_1^2*K_B_3*Ltot^2 - 4*K_A_1^2*K_B_3*Ltot*Rtot + 2*K_A_1^2*K_B_3*Rtot^2 + K_A_1^2*Ltot^2 - 2*K_A_1^2*Ltot*Rtot + K_A_1^2*Rtot^2 + 2*K_A_1*K_B_1*K_B_2*K_B_3*Rtot + 2*K_A_1*K_B_1*K_B_2*Rtot + 2*K_A_1*K_B_1*K_B_3*Rtot + 2*K_A_1*K_B_1*Rtot + 2*K_A_1*K_B_2*K_B_3*Rtot + 2*K_A_1*K_B_2*Rtot + 2*K_A_1*K_B_3*Rtot + 2*K_A_1*Rtot + K_B_1^2*K_B_2^2 + 2*K_B_1^2*K_B_2 + K_B_1^2 + 2*K_B_1*K_B_2^2 + 4*K_B_1*K_B_2 + 2*K_B_1 + K_B_2^2 + 2*K_B_2 + 1)^(1/2) + K_B_1*K_B_2 - K_A_1*Ltot + K_A_1*Rtot - K_A_1*K_B_3*Ltot + K_A_1*K_B_3*Rtot + 1)/(K_B_2 + K_B_3 + K_B_2*K_B_3 + 1) < 0 or not (K_B_1 + K_B_2 + (K_A_1^2*K_B_3^2*Ltot^2 - 2*K_A_1^2*K_B_3^2*Ltot*Rtot + K_A_1^2*K_B_3^2*Rtot^2 + 2*K_A_1^2*K_B_3*Ltot^2 - 4*K_A_1^2*K_B_3*Ltot*Rtot + 2*K_A_1^2*K_B_3*Rtot^2 + K_A_1^2*Ltot^2 - 2*K_A_1^2*Ltot*Rtot + K_A_1^2*Rtot^2 + 2*K_A_1*K_B_1*K_B_2*K_B_3*Ltot + 2*K_A_1*K_B_1*K_B_2*K_B_3*Rtot + 2*K_A_1*K_B_1*K_B_2*Ltot + 2*K_A_1*K_B_1*K_B_2*Rtot + 2*K_A_1*K_B_1*K_B_3*Ltot + 2*K_A_1*K_B_1*K_B_3*Rtot + 2*K_A_1*K_B_1*Ltot + 2*K_A_1*K_B_1*Rtot + 2*K_A_1*K_B_2*K_B_3*Ltot + 2*K_A_1*K_B_2*K_B_3*Rtot + 2*K_A_1*K_B_2*Ltot + 2*K_A_1*K_B_2*Rtot + 2*K_A_1*K_B_3*Ltot + 2*K_A_1*K_B_3*Rtot + 2*K_A_1*Ltot + 2*K_A_1*Rtot + K_B_1^2*K_B_2^2 + 2*K_B_1^2*K_B_2 + K_B_1^2 + 2*K_B_1*K_B_2^2 + 4*K_B_1*K_B_2 + 2*K_B_1 + K_B_2^2 + 2*K_B_2 + 1)^(1/2) + K_B_1*K_B_2 - K_A_1*Ltot + K_A_1*Rtot - K_A_1*K_B_3*Ltot + K_A_1*K_B_3*Rtot + 1)/(K_B_2 + K_B_3 + K_B_2*K_B_3 + 1) < 0 and not (K_B_1 + K_B_2 - (K_A_1^2*K_B_3^2*Ltot^2 - 2*K_A_1^2*K_B_3^2*Ltot*Rtot + K_A_1^2*K_B_3^2*Rtot^2 + 2*K_A_1^2*K_B_3*Ltot^2 - 4*K_A_1^2*K_B_3*Ltot*Rtot + 2*K_A_1^2*K_B_3*Rtot^2 + K_A_1^2*Ltot^2 - 2*K_A_1^2*Ltot*Rtot + K_A_1^2*Rtot^2 + 2*K_A_1*K_B_1*K_B_2*K_B_3*Ltot + 2*K_A_1*K_B_1*K_B_2*K_B_3*Rtot + 2*K_A_1*K_B_1*K_B_2*Ltot + 2*K_A_1*K_B_1*K_B_2*Rtot + 2*K_A_1*K_B_1*K_B_3*Ltot + 2*K_A_1*K_B_1*K_B_3*Rtot + 2*K_A_1*K_B_1*Ltot + 2*K_A_1*K_B_1*Rtot + 2*K_A_1*K_B_2*K_B_3*Ltot + 2*K_A_1*K_B_2*K_B_3*Rtot + 2*K_A_1*K_B_2*Ltot + 2*K_A_1*K_B_2*Rtot + 2*K_A_1*K_B_3*Ltot + 2*K_A_1*K_B_3*Rtot + 2*K_A_1*Ltot + 2*K_A_1*Rtot + K_B_1^2*K_B_2^2 + 2*K_B_1^2*K_B_2 + K_B_1^2 + 2*K_B_1*K_B_2^2 + 4*K_B_1*K_B_2 + 2*K_B_1 + K_B_2^2 + 2*K_B_2 + 1)^(1/2) + K_B_1*K_B_2 - K_A_1*Ltot + K_A_1*Rtot - K_A_1*K_B_3*Ltot + K_A_1*K_B_3*Rtot + 1)/(K_B_2 + K_B_3 + K_B_2*K_B_3 + 1) < 0 and (K_A_1^2*K_B_3^2*Ltot^2 - 2*K_A_1^2*K_B_3^2*Ltot*Rtot + K_A_1^2*K_B_3^2*Rtot^2 + 2*K_A_1^2*K_B_3*Ltot^2 - 4*K_A_1^2*K_B_3*Ltot*Rtot + 2*K_A_1^2*K_B_3*Rtot^2 + K_A_1^2*Ltot^2 - 2*K_A_1^2*Ltot*Rtot + K_A_1^2*Rtot^2 + 2*K_A_1*K_B_1*K_B_2*K_B_3*Ltot + 2*K_A_1*K_B_1*K_B_2*K_B_3*Rtot + 2*K_A_1*K_B_1*K_B_2*Ltot + 2*K_A_1*K_B_1*K_B_2*Rtot + 2*K_A_1*K_B_1*K_B_3*Ltot + 2*K_A_1*K_B_1*K_B_3*Rtot + 2*K_A_1*K_B_1*Ltot + 2*K_A_1*K_B_1*Rtot + 2*K_A_1*K_B_2*K_B_3*Ltot + 2*K_A_1*K_B_2*K_B_3*Rtot + 2*K_A_1*K_B_2*Ltot + 2*K_A_1*K_B_2*Rtot + 2*K_A_1*K_B_3*Ltot + 2*K_A_1*K_B_3*Rtot + 2*K_A_1*Ltot + 2*K_A_1*Rtot + K_B_1^2*K_B_2^2 + 2*K_B_1^2*K_B_2 + K_B_1^2 + 2*K_B_1*K_B_2^2 + 4*K_B_1*K_B_2 + 2*K_B_1 + K_B_2^2 + 2*K_B_2 + 1)^(1/2) + K_A_1*Ltot + K_A_1*K_B_3*Ltot <> K_B_1 + K_B_2 + K_B_1*K_B_2 + K_A_1*Rtot + K_A_1*K_B_3*Rtot + 1 and K_B_1 + K_B_2 + (K_A_1^2*K_B_3^2*Ltot^2 - 2*K_A_1^2*K_B_3^2*Ltot*Rtot + K_A_1^2*K_B_3^2*Rtot^2 + 2*K_A_1^2*K_B_3*Ltot^2 - 4*K_A_1^2*K_B_3*Ltot*Rtot + 2*K_A_1^2*K_B_3*Rtot^2 + K_A_1^2*Ltot^2 - 2*K_A_1^2*Ltot*Rtot + K_A_1^2*Rtot^2 + 2*K_A_1*K_B_1*K_B_2*K_B_3*Ltot + 2*K_A_1*K_B_1*K_B_2*K_B_3*Rtot + 2*K_A_1*K_B_1*K_B_2*Ltot + 2*K_A_1*K_B_1*K_B_2*Rtot + 2*K_A_1*K_B_1*K_B_3*Ltot + 2*K_A_1*K_B_1*K_B_3*Rtot + 2*K_A_1*K_B_1*Ltot + 2*K_A_1*K_B_1*Rtot + 2*K_A_1*K_B_2*K_B_3*Ltot + 2*K_A_1*K_B_2*K_B_3*Rtot + 2*K_A_1*K_B_2*Ltot + 2*K_A_1*K_B_2*Rtot + 2*K_A_1*K_B_3*Ltot + 2*K_A_1*K_B_3*Rtot + 2*K_A_1*Ltot + 2*K_A_1*Rtot + K_B_1^2*K_B_2^2 + 2*K_B_1^2*K_B_2 + K_B_1^2 + 2*K_B_1*K_B_2^2 + 4*K_B_1*K_B_2 + 2*K_B_1 + K_B_2^2 + 2*K_B_2 + 1)^(1/2) + K_B_1*K_B_2 + K_A_1*Rtot + K_A_1*K_B_3*Rtot + 1 <> K_A_1*Ltot + K_A_1*K_B_3*Ltot or not -(K_B_1 + K_B_2 - (K_A_1^2*K_B_3^2*Ltot^2 - 2*K_A_1^2*K_B_3^2*Ltot*Rtot + K_A_1^2*K_B_3^2*Rtot^2 + 2*K_A_1^2*K_B_3*Ltot^2 - 4*K_A_1^2*K_B_3*Ltot*Rtot + 2*K_A_1^2*K_B_3*Rtot^2 + K_A_1^2*Ltot^2 - 2*K_A_1^2*Ltot*Rtot + K_A_1^2*Rtot^2 + 2*K_A_1*K_B_1*K_B_2*K_B_3*Rtot + 2*K_A_1*K_B_1*K_B_2*Rtot + 2*K_A_1*K_B_1*K_B_3*Rtot + 2*K_A_1*K_B_1*Rtot + 2*K_A_1*K_B_2*K_B_3*Rtot + 2*K_A_1*K_B_2*Rtot + 2*K_A_1*K_B_3*Rtot + 2*K_A_1*Rtot + K_B_1^2*K_B_2^2 + 2*K_B_1^2*K_B_2 + K_B_1^2 + 2*K_B_1*K_B_2^2 + 4*K_B_1*K_B_2 + 2*K_B_1 + K_B_2^2 + 2*K_B_2 + 1)^(1/2) + K_B_1*K_B_2 - K_A_1*Ltot + K_A_1*Rtot - K_A_1*K_B_3*Ltot + K_A_1*K_B_3*Rtot + 1)/(2*K_A_1*(K_B_2 + K_B_3 + K_B_2*K_B_3 + 1)) < Ltot and (K_B_1 + K_B_2 - (K_A_1^2*K_B_3^2*Ltot^2 - 2*K_A_1^2*K_B_3^2*Ltot*Rtot + K_A_1^2*K_B_3^2*Rtot^2 + 2*K_A_1^2*K_B_3*Ltot^2 - 4*K_A_1^2*K_B_3*Ltot*Rtot + 2*K_A_1^2*K_B_3*Rtot^2 + K_A_1^2*Ltot^2 - 2*K_A_1^2*Ltot*Rtot + K_A_1^2*Rtot^2 + 2*K_A_1*K_B_1*K_B_2*K_B_3*Rtot + 2*K_A_1*K_B_1*K_B_2*Rtot + 2*K_A_1*K_B_1*K_B_3*Rtot + 2*K_A_1*K_B_1*Rtot + 2*K_A_1*K_B_2*K_B_3*Rtot + 2*K_A_1*K_B_2*Rtot + 2*K_A_1*K_B_3*Rtot + 2*K_A_1*Rtot + K_B_1^2*K_B_2^2 + 2*K_B_1^2*K_B_2 + K_B_1^2 + 2*K_B_1*K_B_2^2 + 4*K_B_1*K_B_2 + 2*K_B_1 + K_B_2^2 + 2*K_B_2 + 1)^(1/2) + K_B_1*K_B_2 - K_A_1*Ltot + K_A_1*Rtot - K_A_1*K_B_3*Ltot + K_A_1*K_B_3*Rtot + 1)/(K_B_2 + K_B_3 + K_B_2*K_B_3 + 1) < 0 and K_B_1 + K_B_2 + (K_A_1^2*K_B_3^2*Ltot^2 - 2*K_A_1^2*K_B_3^2*Ltot*Rtot + K_A_1^2*K_B_3^2*Rtot^2 + 2*K_A_1^2*K_B_3*Ltot^2 - 4*K_A_1^2*K_B_3*Ltot*Rtot + 2*K_A_1^2*K_B_3*Rtot^2 + K_A_1^2*Ltot^2 - 2*K_A_1^2*Ltot*Rtot + K_A_1^2*Rtot^2 + 2*K_A_1*K_B_1*K_B_2*K_B_3*Ltot + 2*K_A_1*K_B_1*K_B_2*K_B_3*Rtot + 2*K_A_1*K_B_1*K_B_2*Ltot + 2*K_A_1*K_B_1*K_B_2*Rtot + 2*K_A_1*K_B_1*K_B_3*Ltot + 2*K_A_1*K_B_1*K_B_3*Rtot + 2*K_A_1*K_B_1*Ltot + 2*K_A_1*K_B_1*Rtot + 2*K_A_1*K_B_2*K_B_3*Ltot + 2*K_A_1*K_B_2*K_B_3*Rtot + 2*K_A_1*K_B_2*Ltot + 2*K_A_1*K_B_2*Rtot + 2*K_A_1*K_B_3*Ltot + 2*K_A_1*K_B_3*Rtot + 2*K_A_1*Ltot + 2*K_A_1*Rtot + K_B_1^2*K_B_2^2 + 2*K_B_1^2*K_B_2 + K_B_1^2 + 2*K_B_1*K_B_2^2 + 4*K_B_1*K_B_2 + 2*K_B_1 + K_B_2^2 + 2*K_B_2 + 1)^(1/2) + K_B_1*K_B_2 + K_A_1*Rtot + K_A_1*K_B_3*Rtot + 1 = K_A_1*Ltot + K_A_1*K_B_3*Ltot and (K_A_1^2*K_B_3^2*Ltot^2 - 2*K_A_1^2*K_B_3^2*Ltot*Rtot + K_A_1^2*K_B_3^2*Rtot^2 + 2*K_A_1^2*K_B_3*Ltot^2 - 4*K_A_1^2*K_B_3*Ltot*Rtot + 2*K_A_1^2*K_B_3*Rtot^2 + K_A_1^2*Ltot^2 - 2*K_A_1^2*Ltot*Rtot + K_A_1^2*Rtot^2 + 2*K_A_1*K_B_1*K_B_2*K_B_3*Ltot + 2*K_A_1*K_B_1*K_B_2*K_B_3*Rtot + 2*K_A_1*K_B_1*K_B_2*Ltot + 2*K_A_1*K_B_1*K_B_2*Rtot + 2*K_A_1*K_B_1*K_B_3*Ltot + 2*K_A_1*K_B_1*K_B_3*Rtot + 2*K_A_1*K_B_1*Ltot + 2*K_A_1*K_B_1*Rtot + 2*K_A_1*K_B_2*K_B_3*Ltot + 2*K_A_1*K_B_2*K_B_3*Rtot + 2*K_A_1*K_B_2*Ltot + 2*K_A_1*K_B_2*Rtot + 2*K_A_1*K_B_3*Ltot + 2*K_A_1*K_B_3*Rtot + 2*K_A_1*Ltot + 2*K_A_1*Rtot + K_B_1^2*K_B_2^2 + 2*K_B_1^2*K_B_2 + K_B_1^2 + 2*K_B_1*K_B_2^2 + 4*K_B_1*K_B_2 + 2*K_B_1 + K_B_2^2 + 2*K_B_2 + 1)^(1/2) + K_A_1*Ltot + K_A_1*K_B_3*Ltot <> K_B_1 + K_B_2 + K_B_1*K_B_2 + K_A_1*Rtot + K_A_1*K_B_3*Rtot + 1 or not -(K_B_1 + K_B_2 + (K_A_1^2*K_B_3^2*Ltot^2 - 2*K_A_1^2*K_B_3^2*Ltot*Rtot + K_A_1^2*K_B_3^2*Rtot^2 + 2*K_A_1^2*K_B_3*Ltot^2 - 4*K_A_1^2*K_B_3*Ltot*Rtot + 2*K_A_1^2*K_B_3*Rtot^2 + K_A_1^2*Ltot^2 - 2*K_A_1^2*Ltot*Rtot + K_A_1^2*Rtot^2 + 2*K_A_1*K_B_1*K_B_2*K_B_3*Ltot + 2*K_A_1*K_B_1*K_B_2*K_B_3*Rtot + 2*K_A_1*K_B_1*K_B_2*Ltot + 2*K_A_1*K_B_1*K_B_2*Rtot + 2*K_A_1*K_B_1*K_B_3*Ltot + 2*K_A_1*K_B_1*K_B_3*Rtot + 2*K_A_1*K_B_1*Ltot + 2*K_A_1*K_B_1*Rtot + 2*K_A_1*K_B_2*K_B_3*Ltot + 2*K_A_1*K_B_2*K_B_3*Rtot + 2*K_A_1*K_B_2*Ltot + 2*K_A_1*K_B_2*Rtot + 2*K_A_1*K_B_3*Ltot + 2*K_A_1*K_B_3*Rtot + 2*K_A_1*Ltot + 2*K_A_1*Rtot + K_B_1^2*K_B_2^2 + 2*K_B_1^2*K_B_2 + K_B_1^2 + 2*K_B_1*K_B_2^2 + 4*K_B_1*K_B_2 + 2*K_B_1 + K_B_2^2 + 2*K_B_2 + 1)^(1/2) + K_B_1*K_B_2 - K_A_1*Ltot + K_A_1*Rtot - K_A_1*K_B_3*Ltot + K_A_1*K_B_3*Rtot + 1)/(2*K_A_1*(K_B_2 + K_B_3 + K_B_2*K_B_3 + 1)) < Ltot and (K_B_1 + K_B_2 + (K_A_1^2*K_B_3^2*Ltot^2 - 2*K_A_1^2*K_B_3^2*Ltot*Rtot + K_A_1^2*K_B_3^2*Rtot^2 + 2*K_A_1^2*K_B_3*Ltot^2 - 4*K_A_1^2*K_B_3*Ltot*Rtot + 2*K_A_1^2*K_B_3*Rtot^2 + K_A_1^2*Ltot^2 - 2*K_A_1^2*Ltot*Rtot + K_A_1^2*Rtot^2 + 2*K_A_1*K_B_1*K_B_2*K_B_3*Ltot + 2*K_A_1*K_B_1*K_B_2*K_B_3*Rtot + 2*K_A_1*K_B_1*K_B_2*Ltot + 2*K_A_1*K_B_1*K_B_2*Rtot + 2*K_A_1*K_B_1*K_B_3*Ltot + 2*K_A_1*K_B_1*K_B_3*Rtot + 2*K_A_1*K_B_1*Ltot + 2*K_A_1*K_B_1*Rtot + 2*K_A_1*K_B_2*K_B_3*Ltot + 2*K_A_1*K_B_2*K_B_3*Rtot + 2*K_A_1*K_B_2*Ltot + 2*K_A_1*K_B_2*Rtot + 2*K_A_1*K_B_3*Ltot + 2*K_A_1*K_B_3*Rtot + 2*K_A_1*Ltot + 2*K_A_1*Rtot + K_B_1^2*K_B_2^2 + 2*K_B_1^2*K_B_2 + K_B_1^2 + 2*K_B_1*K_B_2^2 + 4*K_B_1*K_B_2 + 2*K_B_1 + K_B_2^2 + 2*K_B_2 + 1)^(1/2) + K_B_1*K_B_2 - K_A_1*Ltot + K_A_1*Rtot - K_A_1*K_B_3*Ltot + K_A_1*K_B_3*Rtot + 1)/(K_B_2 + K_B_3 + K_B_2*K_B_3 + 1) < 0 and not (K_B_1 + K_B_2 - (K_A_1^2*K_B_3^2*Ltot^2 - 2*K_A_1^2*K_B_3^2*Ltot*Rtot + K_A_1^2*K_B_3^2*Rtot^2 + 2*K_A_1^2*K_B_3*Ltot^2 - 4*K_A_1^2*K_B_3*Ltot*Rtot + 2*K_A_1^2*K_B_3*Rtot^2 + K_A_1^2*Ltot^2 - 2*K_A_1^2*Ltot*Rtot + K_A_1^2*Rtot^2 + 2*K_A_1*K_B_1*K_B_2*K_B_3*Ltot + 2*K_A_1*K_B_1*K_B_2*K_B_3*Rtot + 2*K_A_1*K_B_1*K_B_2*Ltot + 2*K_A_1*K_B_1*K_B_2*Rtot + 2*K_A_1*K_B_1*K_B_3*Ltot + 2*K_A_1*K_B_1*K_B_3*Rtot + 2*K_A_1*K_B_1*Ltot + 2*K_A_1*K_B_1*Rtot + 2*K_A_1*K_B_2*K_B_3*Ltot + 2*K_A_1*K_B_2*K_B_3*Rtot + 2*K_A_1*K_B_2*Ltot + 2*K_A_1*K_B_2*Rtot + 2*K_A_1*K_B_3*Ltot + 2*K_A_1*K_B_3*Rtot + 2*K_A_1*Ltot + 2*K_A_1*Rtot + K_B_1^2*K_B_2^2 + 2*K_B_1^2*K_B_2 + K_B_1^2 + 2*K_B_1*K_B_2^2 + 4*K_B_1*K_B_2 + 2*K_B_1 + K_B_2^2 + 2*K_B_2 + 1)^(1/2) + K_B_1*K_B_2 - K_A_1*Ltot + K_A_1*Rtot - K_A_1*K_B_3*Ltot + K_A_1*K_B_3*Rtot + 1)/(K_B_2 + K_B_3 + K_B_2*K_B_3 + 1) < 0 and (K_A_1^2*K_B_3^2*Ltot^2 - 2*K_A_1^2*K_B_3^2*Ltot*Rtot + K_A_1^2*K_B_3^2*Rtot^2 + 2*K_A_1^2*K_B_3*Ltot^2 - 4*K_A_1^2*K_B_3*Ltot*Rtot + 2*K_A_1^2*K_B_3*Rtot^2 + K_A_1^2*Ltot^2 - 2*K_A_1^2*Ltot*Rtot + K_A_1^2*Rtot^2 + 2*K_A_1*K_B_1*K_B_2*K_B_3*Ltot + 2*K_A_1*K_B_1*K_B_2*K_B_3*Rtot + 2*K_A_1*K_B_1*K_B_2*Ltot + 2*K_A_1*K_B_1*K_B_2*Rtot + 2*K_A_1*K_B_1*K_B_3*Ltot + 2*K_A_1*K_B_1*K_B_3*Rtot + 2*K_A_1*K_B_1*Ltot + 2*K_A_1*K_B_1*Rtot + 2*K_A_1*K_B_2*K_B_3*Ltot + 2*K_A_1*K_B_2*K_B_3*Rtot + 2*K_A_1*K_B_2*Ltot + 2*K_A_1*K_B_2*Rtot + 2*K_A_1*K_B_3*Ltot + 2*K_A_1*K_B_3*Rtot + 2*K_A_1*Ltot + 2*K_A_1*Rtot + K_B_1^2*K_B_2^2 + 2*K_B_1^2*K_B_2 + K_B_1^2 + 2*K_B_1*K_B_2^2 + 4*K_B_1*K_B_2 + 2*K_B_1 + K_B_2^2 + 2*K_B_2 + 1)^(1/2) + K_A_1*Ltot + K_A_1*K_B_3*Ltot <> K_B_1 + K_B_2 + K_B_1*K_B_2 + K_A_1*Rtot + K_A_1*K_B_3*Rtot + 1 and K_B_1 + K_B_2 + (K_A_1^2*K_B_3^2*Ltot^2 - 2*K_A_1^2*K_B_3^2*Ltot*Rtot + K_A_1^2*K_B_3^2*Rtot^2 + 2*K_A_1^2*K_B_3*Ltot^2 - 4*K_A_1^2*K_B_3*Ltot*Rtot + 2*K_A_1^2*K_B_3*Rtot^2 + K_A_1^2*Ltot^2 - 2*K_A_1^2*Ltot*Rtot + K_A_1^2*Rtot^2 + 2*K_A_1*K_B_1*K_B_2*K_B_3*Ltot + 2*K_A_1*K_B_1*K_B_2*K_B_3*Rtot + 2*K_A_1*K_B_1*K_B_2*Ltot + 2*K_A_1*K_B_1*K_B_2*Rtot + 2*K_A_1*K_B_1*K_B_3*Ltot + 2*K_A_1*K_B_1*K_B_3*Rtot + 2*K_A_1*K_B_1*Ltot + 2*K_A_1*K_B_1*Rtot + 2*K_A_1*K_B_2*K_B_3*Ltot + 2*K_A_1*K_B_2*K_B_3*Rtot + 2*K_A_1*K_B_2*Ltot + 2*K_A_1*K_B_2*Rtot + 2*K_A_1*K_B_3*Ltot + 2*K_A_1*K_B_3*Rtot + 2*K_A_1*Ltot + 2*K_A_1*Rtot + K_B_1^2*K_B_2^2 + 2*K_B_1^2*K_B_2 + K_B_1^2 + 2*K_B_1*K_B_2^2 + 4*K_B_1*K_B_2 + 2*K_B_1 + K_B_2^2 + 2*K_B_2 + 1)^(1/2) + K_B_1*K_B_2 + K_A_1*Rtot + K_A_1*K_B_3*Rtot + 1 <> K_A_1*Ltot + K_A_1*K_B_3*Ltot or not (K_B_1 + K_B_2 + (K_A_1^2*K_B_3^2*Ltot^2 - 2*K_A_1^2*K_B_3^2*Ltot*Rtot + K_A_1^2*K_B_3^2*Rtot^2 + 2*K_A_1^2*K_B_3*Ltot^2 - 4*K_A_1^2*K_B_3*Ltot*Rtot + 2*K_A_1^2*K_B_3*Rtot^2 + K_A_1^2*Ltot^2 - 2*K_A_1^2*Ltot*Rtot + K_A_1^2*Rtot^2 + 2*K_A_1*K_B_1*K_B_2*K_B_3*Ltot + 2*K_A_1*K_B_1*K_B_2*K_B_3*Rtot + 2*K_A_1*K_B_1*K_B_2*Ltot + 2*K_A_1*K_B_1*K_B_2*Rtot + 2*K_A_1*K_B_1*K_B_3*Ltot + 2*K_A_1*K_B_1*K_B_3*Rtot + 2*K_A_1*K_B_1*Ltot + 2*K_A_1*K_B_1*Rtot + 2*K_A_1*K_B_2*K_B_3*Ltot + 2*K_A_1*K_B_2*K_B_3*Rtot + 2*K_A_1*K_B_2*Ltot + 2*K_A_1*K_B_2*Rtot + 2*K_A_1*K_B_3*Ltot + 2*K_A_1*K_B_3*Rtot + 2*K_A_1*Ltot + 2*K_A_1*Rtot + K_B_1^2*K_B_2^2 + 2*K_B_1^2*K_B_2 + K_B_1^2 + 2*K_B_1*K_B_2^2 + 4*K_B_1*K_B_2 + 2*K_B_1 + K_B_2^2 + 2*K_B_2 + 1)^(1/2) + K_B_1*K_B_2 - K_A_1*Ltot + K_A_1*Rtot - K_A_1*K_B_3*Ltot + K_A_1*K_B_3*Rtot + 1)/(K_B_2 + K_B_3 + K_B_2*K_B_3 + 1) < 0 and not -(K_B_1 + K_B_2 - (K_A_1^2*K_B_3^2*Ltot^2 - 2*K_A_1^2*K_B_3^2*Ltot*Rtot + K_A_1^2*K_B_3^2*Rtot^2 + 2*K_A_1^2*K_B_3*Ltot^2 - 4*K_A_1^2*K_B_3*Ltot*Rtot + 2*K_A_1^2*K_B_3*Rtot^2 + K_A_1^2*Ltot^2 - 2*K_A_1^2*Ltot*Rtot + K_A_1^2*Rtot^2 + 2*K_A_1*K_B_1*K_B_2*K_B_3*Ltot + 2*K_A_1*K_B_1*K_B_2*K_B_3*Rtot + 2*K_A_1*K_B_1*K_B_2*Ltot + 2*K_A_1*K_B_1*K_B_2*Rtot + 2*K_A_1*K_B_1*K_B_3*Ltot + 2*K_A_1*K_B_1*K_B_3*Rtot + 2*K_A_1*K_B_1*Ltot + 2*K_A_1*K_B_1*Rtot + 2*K_A_1*K_B_2*K_B_3*Ltot + 2*K_A_1*K_B_2*K_B_3*Rtot + 2*K_A_1*K_B_2*Ltot + 2*K_A_1*K_B_2*Rtot + 2*K_A_1*K_B_3*Ltot + 2*K_A_1*K_B_3*Rtot + 2*K_A_1*Ltot + 2*K_A_1*Rtot + K_B_1^2*K_B_2^2 + 2*K_B_1^2*K_B_2 + K_B_1^2 + 2*K_B_1*K_B_2^2 + 4*K_B_1*K_B_2 + 2*K_B_1 + K_B_2^2 + 2*K_B_2 + 1)^(1/2) + K_B_1*K_B_2 - K_A_1*Ltot + K_A_1*Rtot - K_A_1*K_B_3*Ltot + K_A_1*K_B_3*Rtot + 1)/(2*K_A_1*(K_B_2 + K_B_3 + K_B_2*K_B_3 + 1)) < Ltot and (K_B_1 + K_B_2 - (K_A_1^2*K_B_3^2*Ltot^2 - 2*K_A_1^2*K_B_3^2*Ltot*Rtot + K_A_1^2*K_B_3^2*Rtot^2 + 2*K_A_1^2*K_B_3*Ltot^2 - 4*K_A_1^2*K_B_3*Ltot*Rtot + 2*K_A_1^2*K_B_3*Rtot^2 + K_A_1^2*Ltot^2 - 2*K_A_1^2*Ltot*Rtot + K_A_1^2*Rtot^2 + 2*K_A_1*K_B_1*K_B_2*K_B_3*Ltot + 2*K_A_1*K_B_1*K_B_2*K_B_3*Rtot + 2*K_A_1*K_B_1*K_B_2*Ltot + 2*K_A_1*K_B_1*K_B_2*Rtot + 2*K_A_1*K_B_1*K_B_3*Ltot + 2*K_A_1*K_B_1*K_B_3*Rtot + 2*K_A_1*K_B_1*Ltot + 2*K_A_1*K_B_1*Rtot + 2*K_A_1*K_B_2*K_B_3*Ltot + 2*K_A_1*K_B_2*K_B_3*Rtot + 2*K_A_1*K_B_2*Ltot + 2*K_A_1*K_B_2*Rtot + 2*K_A_1*K_B_3*Ltot + 2*K_A_1*K_B_3*Rtot + 2*K_A_1*Ltot + 2*K_A_1*Rtot + K_B_1^2*K_B_2^2 + 2*K_B_1^2*K_B_2 + K_B_1^2 + 2*K_B_1*K_B_2^2 + 4*K_B_1*K_B_2 + 2*K_B_1 + K_B_2^2 + 2*K_B_2 + 1)^(1/2) + K_B_1*K_B_2 - K_A_1*Ltot + K_A_1*Rtot - K_A_1*K_B_3*Ltot + K_A_1*K_B_3*Rtot + 1)/(K_B_2 + K_B_3 + K_B_2*K_B_3 + 1) < 0 and (K_A_1^2*K_B_3^2*Ltot^2 - 2*K_A_1^2*K_B_3^2*Ltot*Rtot + K_A_1^2*K_B_3^2*Rtot^2 + 2*K_A_1^2*K_B_3*Ltot^2 - 4*K_A_1^2*K_B_3*Ltot*Rtot + 2*K_A_1^2*K_B_3*Rtot^2 + K_A_1^2*Ltot^2 - 2*K_A_1^2*Ltot*Rtot + K_A_1^2*Rtot^2 + 2*K_A_1*K_B_1*K_B_2*K_B_3*Ltot + 2*K_A_1*K_B_1*K_B_2*K_B_3*Rtot + 2*K_A_1*K_B_1*K_B_2*Ltot + 2*K_A_1*K_B_1*K_B_2*Rtot + 2*K_A_1*K_B_1*K_B_3*Ltot + 2*K_A_1*K_B_1*K_B_3*Rtot + 2*K_A_1*K_B_1*Ltot + 2*K_A_1*K_B_1*Rtot + 2*K_A_1*K_B_2*K_B_3*Ltot + 2*K_A_1*K_B_2*K_B_3*Rtot + 2*K_A_1*K_B_2*Ltot + 2*K_A_1*K_B_2*Rtot + 2*K_A_1*K_B_3*Ltot + 2*K_A_1*K_B_3*Rtot + 2*K_A_1*Ltot + 2*K_A_1*Rtot + K_B_1^2*K_B_2^2 + 2*K_B_1^2*K_B_2 + K_B_1^2 + 2*K_B_1*K_B_2^2 + 4*K_B_1*K_B_2 + 2*K_B_1 + K_B_2^2 + 2*K_B_2 + 1)^(1/2) + K_A_1*Ltot + K_A_1*K_B_3*Ltot <> K_B_1 + K_B_2 + K_B_1*K_B_2 + K_A_1*Rtot + K_A_1*K_B_3*Rtot + 1 and K_B_1 + K_B_2 + (K_A_1^2*K_B_3^2*Ltot^2 - 2*K_A_1^2*K_B_3^2*Ltot*Rtot + K_A_1^2*K_B_3^2*Rtot^2 + 2*K_A_1^2*K_B_3*Ltot^2 - 4*K_A_1^2*K_B_3*Ltot*Rtot + 2*K_A_1^2*K_B_3*Rtot^2 + K_A_1^2*Ltot^2 - 2*K_A_1^2*Ltot*Rtot + K_A_1^2*Rtot^2 + 2*K_A_1*K_B_1*K_B_2*K_B_3*Ltot + 2*K_A_1*K_B_1*K_B_2*K_B_3*Rtot + 2*K_A_1*K_B_1*K_B_2*Ltot + 2*K_A_1*K_B_1*K_B_2*Rtot + 2*K_A_1*K_B_1*K_B_3*Ltot + 2*K_A_1*K_B_1*K_B_3*Rtot + 2*K_A_1*K_B_1*Ltot + 2*K_A_1*K_B_1*Rtot + 2*K_A_1*K_B_2*K_B_3*Ltot + 2*K_A_1*K_B_2*K_B_3*Rtot + 2*K_A_1*K_B_2*Ltot + 2*K_A_1*K_B_2*Rtot + 2*K_A_1*K_B_3*Ltot + 2*K_A_1*K_B_3*Rtot + 2*K_A_1*Ltot + 2*K_A_1*Rtot + K_B_1^2*K_B_2^2 + 2*K_B_1^2*K_B_2 + K_B_1^2 + 2*K_B_1*K_B_2^2 + 4*K_B_1*K_B_2 + 2*K_B_1 + K_B_2^2 + 2*K_B_2 + 1)^(1/2) + K_B_1*K_B_2 + K_A_1*Rtot + K_A_1*K_B_3*Rtot + 1 <> K_A_1*Ltot + K_A_1*K_B_3*Ltot or K_A_1^2*K_B_3^2*Ltot^2 + K_A_1^2*K_B_3^2*Rtot^2 + 2*K_A_1^2*K_B_3*Ltot^2 + 2*K_A_1^2*K_B_3*Rtot^2 + K_A_1^2*Ltot^2 + K_A_1^2*Rtot^2 + 2*K_A_1*K_B_1*K_B_2*K_B_3*Ltot + 2*K_A_1*K_B_1*K_B_2*K_B_3*Rtot + 2*K_A_1*K_B_1*K_B_2*Ltot + 2*K_A_1*K_B_1*K_B_2*Rtot + 2*K_A_1*K_B_1*K_B_3*Ltot + 2*K_A_1*K_B_1*K_B_3*Rtot + 2*K_A_1*K_B_1*Ltot + 2*K_A_1*K_B_1*Rtot + 2*K_A_1*K_B_2*K_B_3*Ltot + 2*K_A_1*K_B_2*K_B_3*Rtot + 2*K_A_1*K_B_2*Ltot + 2*K_A_1*K_B_2*Rtot + 2*K_A_1*K_B_3*Ltot + 2*K_A_1*K_B_3*Rtot + 2*K_A_1*Ltot + 2*K_A_1*Rtot + K_B_1^2*K_B_2^2 + 2*K_B_1^2*K_B_2 + K_B_1^2 + 2*K_B_1*K_B_2^2 + 4*K_B_1*K_B_2 + 2*K_B_1 + K_B_2^2 + 2*K_B_2 + 1 < 2*Ltot*Rtot*K_A_1^2*K_B_3^2 + 4*Ltot*Rtot*K_A_1^2*K_B_3 + 2*Ltot*Rtot*K_A_1^2 and (not -(K_B_1 + K_B_2 - (K_A_1^2*K_B_3^2*Ltot^2 - 2*K_A_1^2*K_B_3^2*Ltot*Rtot + K_A_1^2*K_B_3^2*Rtot^2 + 2*K_A_1^2*K_B_3*Ltot^2 - 4*K_A_1^2*K_B_3*Ltot*Rtot + 2*K_A_1^2*K_B_3*Rtot^2 + K_A_1^2*Ltot^2 - 2*K_A_1^2*Ltot*Rtot + K_A_1^2*Rtot^2 + 2*K_A_1*K_B_1*K_B_2*K_B_3*Ltot + 2*K_A_1*K_B_1*K_B_2*K_B_3*Rtot + 2*K_A_1*K_B_1*K_B_2*Ltot + 2*K_A_1*K_B_1*K_B_2*Rtot + 2*K_A_1*K_B_1*K_B_3*Ltot + 2*K_A_1*K_B_1*K_B_3*Rtot + 2*K_A_1*K_B_1*Ltot + 2*K_A_1*K_B_1*Rtot + 2*K_A_1*K_B_2*K_B_3*Ltot + 2*K_A_1*K_B_2*K_B_3*Rtot + 2*K_A_1*K_B_2*Ltot + 2*K_A_1*K_B_2*Rtot + 2*K_A_1*K_B_3*Ltot + 2*K_A_1*K_B_3*Rtot + 2*K_A_1*Ltot + 2*K_A_1*Rtot + K_B_1^2*K_B_2^2 + 2*K_B_1^2*K_B_2 + K_B_1^2 + 2*K_B_1*K_B_2^2 + 4*K_B_1*K_B_2 + 2*K_B_1 + K_B_2^2 + 2*K_B_2 + 1)^(1/2) + K_B_1*K_B_2 - K_A_1*Ltot + K_A_1*Rtot - K_A_1*K_B_3*Ltot + K_A_1*K_B_3*Rtot + 1)/(2*K_A_1*(K_B_2 + K_B_3 + K_B_2*K_B_3 + 1)) < Ltot or not (K_B_1 + K_B_2 - (K_A_1^2*K_B_3^2*Ltot^2 - 2*K_A_1^2*K_B_3^2*Ltot*Rtot + K_A_1^2*K_B_3^2*Rtot^2 + 2*K_A_1^2*K_B_3*Ltot^2 - 4*K_A_1^2*K_B_3*Ltot*Rtot + 2*K_A_1^2*K_B_3*Rtot^2 + K_A_1^2*Ltot^2 - 2*K_A_1^2*Ltot*Rtot + K_A_1^2*Rtot^2 + 2*K_A_1*K_B_1*K_B_2*K_B_3*Ltot + 2*K_A_1*K_B_1*K_B_2*K_B_3*Rtot + 2*K_A_1*K_B_1*K_B_2*Ltot + 2*K_A_1*K_B_1*K_B_2*Rtot + 2*K_A_1*K_B_1*K_B_3*Ltot + 2*K_A_1*K_B_1*K_B_3*Rtot + 2*K_A_1*K_B_1*Ltot + 2*K_A_1*K_B_1*Rtot + 2*K_A_1*K_B_2*K_B_3*Ltot + 2*K_A_1*K_B_2*K_B_3*Rtot + 2*K_A_1*K_B_2*Ltot + 2*K_A_1*K_B_2*Rtot + 2*K_A_1*K_B_3*Ltot + 2*K_A_1*K_B_3*Rtot + 2*K_A_1*Ltot + 2*K_A_1*Rtot + K_B_1^2*K_B_2^2 + 2*K_B_1^2*K_B_2 + K_B_1^2 + 2*K_B_1*K_B_2^2 + 4*K_B_1*K_B_2 + 2*K_B_1 + K_B_2^2 + 2*K_B_2 + 1)^(1/2) + K_B_1*K_B_2 - K_A_1*Ltot + K_A_1*Rtot - K_A_1*K_B_3*Ltot + K_A_1*K_B_3*Rtot + 1)/(K_B_2 + K_B_3 + K_B_2*K_B_3 + 1) < 0) and -(K_B_1 + K_B_2 + (K_A_1^2*K_B_3^2*Ltot^2 - 2*K_A_1^2*K_B_3^2*Ltot*Rtot + K_A_1^2*K_B_3^2*Rtot^2 + 2*K_A_1^2*K_B_3*Ltot^2 - 4*K_A_1^2*K_B_3*Ltot*Rtot + 2*K_A_1^2*K_B_3*Rtot^2 + K_A_1^2*Ltot^2 - 2*K_A_1^2*Ltot*Rtot + K_A_1^2*Rtot^2 + 2*K_A_1*K_B_1*K_B_2*K_B_3*Ltot + 2*K_A_1*K_B_1*K_B_2*K_B_3*Rtot + 2*K_A_1*K_B_1*K_B_2*Ltot + 2*K_A_1*K_B_1*K_B_2*Rtot + 2*K_A_1*K_B_1*K_B_3*Ltot + 2*K_A_1*K_B_1*K_B_3*Rtot + 2*K_A_1*K_B_1*Ltot + 2*K_A_1*K_B_1*Rtot + 2*K_A_1*K_B_2*K_B_3*Ltot + 2*K_A_1*K_B_2*K_B_3*Rtot + 2*K_A_1*K_B_2*Ltot + 2*K_A_1*K_B_2*Rtot + 2*K_A_1*K_B_3*Ltot + 2*K_A_1*K_B_3*Rtot + 2*K_A_1*Ltot + 2*K_A_1*Rtot + K_B_1^2*K_B_2^2 + 2*K_B_1^2*K_B_2 + K_B_1^2 + 2*K_B_1*K_B_2^2 + 4*K_B_1*K_B_2 + 2*K_B_1 + K_B_2^2 + 2*K_B_2 + 1)^(1/2) + K_B_1*K_B_2 - K_A_1*Ltot + K_A_1*Rtot - K_A_1*K_B_3*Ltot + K_A_1*K_B_3*Rtot + 1)/(2*K_A_1*(K_B_2 + K_B_3 + K_B_2*K_B_3 + 1)) < Ltot and (K_B_1 + K_B_2 + (K_A_1^2*K_B_3^2*Ltot^2 - 2*K_A_1^2*K_B_3^2*Ltot*Rtot + K_A_1^2*K_B_3^2*Rtot^2 + 2*K_A_1^2*K_B_3*Ltot^2 - 4*K_A_1^2*K_B_3*Ltot*Rtot + 2*K_A_1^2*K_B_3*Rtot^2 + K_A_1^2*Ltot^2 - 2*K_A_1^2*Ltot*Rtot + K_A_1^2*Rtot^2 + 2*K_A_1*K_B_1*K_B_2*K_B_3*Ltot + 2*K_A_1*K_B_1*K_B_2*K_B_3*Rtot + 2*K_A_1*K_B_1*K_B_2*Ltot + 2*K_A_1*K_B_1*K_B_2*Rtot + 2*K_A_1*K_B_1*K_B_3*Ltot + 2*K_A_1*K_B_1*K_B_3*Rtot + 2*K_A_1*K_B_1*Ltot + 2*K_A_1*K_B_1*Rtot + 2*K_A_1*K_B_2*K_B_3*Ltot + 2*K_A_1*K_B_2*K_B_3*Rtot + 2*K_A_1*K_B_2*Ltot + 2*K_A_1*K_B_2*Rtot + 2*K_A_1*K_B_3*Ltot + 2*K_A_1*K_B_3*Rtot + 2*K_A_1*Ltot + 2*K_A_1*Rtot + K_B_1^2*K_B_2^2 + 2*K_B_1^2*K_B_2 + K_B_1^2 + 2*K_B_1*K_B_2^2 + 4*K_B_1*K_B_2 + 2*K_B_1 + K_B_2^2 + 2*K_B_2 + 1)^(1/2) + K_B_1*K_B_2 - K_A_1*Ltot + K_A_1*Rtot - K_A_1*K_B_3*Ltot + K_A_1*K_B_3*Rtot + 1)/(K_B_2 + K_B_3 + K_B_2*K_B_3 + 1) < 0 and (K_A_1^2*K_B_3^2*Ltot^2 - 2*K_A_1^2*K_B_3^2*Ltot*Rtot + K_A_1^2*K_B_3^2*Rtot^2 + 2*K_A_1^2*K_B_3*Ltot^2 - 4*K_A_1^2*K_B_3*Ltot*Rtot + 2*K_A_1^2*K_B_3*Rtot^2 + K_A_1^2*Ltot^2 - 2*K_A_1^2*Ltot*Rtot + K_A_1^2*Rtot^2 + 2*K_A_1*K_B_1*K_B_2*K_B_3*Ltot + 2*K_A_1*K_B_1*K_B_2*K_B_3*Rtot + 2*K_A_1*K_B_1*K_B_2*Ltot + 2*K_A_1*K_B_1*K_B_2*Rtot + 2*K_A_1*K_B_1*K_B_3*Ltot + 2*K_A_1*K_B_1*K_B_3*Rtot + 2*K_A_1*K_B_1*Ltot + 2*K_A_1*K_B_1*Rtot + 2*K_A_1*K_B_2*K_B_3*Ltot + 2*K_A_1*K_B_2*K_B_3*Rtot + 2*K_A_1*K_B_2*Ltot + 2*K_A_1*K_B_2*Rtot + 2*K_A_1*K_B_3*Ltot + 2*K_A_1*K_B_3*Rtot + 2*K_A_1*Ltot + 2*K_A_1*Rtot + K_B_1^2*K_B_2^2 + 2*K_B_1^2*K_B_2 + K_B_1^2 + 2*K_B_1*K_B_2^2 + 4*K_B_1*K_B_2 + 2*K_B_1 + K_B_2^2 + 2*K_B_2 + 1)^(1/2) + K_A_1*Ltot + K_A_1*K_B_3*Ltot <> K_B_1 + K_B_2 + K_B_1*K_B_2 + K_A_1*Rtot + K_A_1*K_B_3*Rtot + 1 and K_B_1 + K_B_2 + (K_A_1^2*K_B_3^2*Ltot^2 - 2*K_A_1^2*K_B_3^2*Ltot*Rtot + K_A_1^2*K_B_3^2*Rtot^2 + 2*K_A_1^2*K_B_3*Ltot^2 - 4*K_A_1^2*K_B_3*Ltot*Rtot + 2*K_A_1^2*K_B_3*Rtot^2 + K_A_1^2*Ltot^2 - 2*K_A_1^2*Ltot*Rtot + K_A_1^2*Rtot^2 + 2*K_A_1*K_B_1*K_B_2*K_B_3*Ltot + 2*K_A_1*K_B_1*K_B_2*K_B_3*Rtot + 2*K_A_1*K_B_1*K_B_2*Ltot + 2*K_A_1*K_B_1*K_B_2*Rtot + 2*K_A_1*K_B_1*K_B_3*Ltot + 2*K_A_1*K_B_1*K_B_3*Rtot + 2*K_A_1*K_B_1*Ltot + 2*K_A_1*K_B_1*Rtot + 2*K_A_1*K_B_2*K_B_3*Ltot + 2*K_A_1*K_B_2*K_B_3*Rtot + 2*K_A_1*K_B_2*Ltot + 2*K_A_1*K_B_2*Rtot + 2*K_A_1*K_B_3*Ltot + 2*K_A_1*K_B_3*Rtot + 2*K_A_1*Ltot + 2*K_A_1*Rtot + K_B_1^2*K_B_2^2 + 2*K_B_1^2*K_B_2 + K_B_1^2 + 2*K_B_1*K_B_2^2 + 4*K_B_1*K_B_2 + 2*K_B_1 + K_B_2^2 + 2*K_B_2 + 1)^(1/2) + K_B_1*K_B_2 + K_A_1*Rtot + K_A_1*K_B_3*Rtot + 1 <> K_A_1*Ltot + K_A_1*K_B_3*Ltot or K_A_1^2*K_B_3^2*Ltot^2 + K_A_1^2*K_B_3^2*Rtot^2 + 2*K_A_1^2*K_B_3*Ltot^2 + 2*K_A_1^2*K_B_3*Rtot^2 + K_A_1^2*Ltot^2 + K_A_1^2*Rtot^2 + 2*K_A_1*K_B_1*K_B_2*K_B_3*Ltot + 2*K_A_1*K_B_1*K_B_2*K_B_3*Rtot + 2*K_A_1*K_B_1*K_B_2*Ltot + 2*K_A_1*K_B_1*K_B_2*Rtot + 2*K_A_1*K_B_1*K_B_3*Ltot + 2*K_A_1*K_B_1*K_B_3*Rtot + 2*K_A_1*K_B_1*Ltot + 2*K_A_1*K_B_1*Rtot + 2*K_A_1*K_B_2*K_B_3*Ltot + 2*K_A_1*K_B_2*K_B_3*Rtot + 2*K_A_1*K_B_2*Ltot + 2*K_A_1*K_B_2*Rtot + 2*K_A_1*K_B_3*Ltot + 2*K_A_1*K_B_3*Rtot + 2*K_A_1*Ltot + 2*K_A_1*Rtot + K_B_1^2*K_B_2^2 + 2*K_B_1^2*K_B_2 + K_B_1^2 + 2*K_B_1*K_B_2^2 + 4*K_B_1*K_B_2 + 2*K_B_1 + K_B_2^2 + 2*K_B_2 + 1 < 2*Ltot*Rtot*K_A_1^2*K_B_3^2 + 4*Ltot*Rtot*K_A_1^2*K_B_3 + 2*Ltot*Rtot*K_A_1^2 and (not -(K_B_1 + K_B_2 + (K_A_1^2*K_B_3^2*Ltot^2 - 2*K_A_1^2*K_B_3^2*Ltot*Rtot + K_A_1^2*K_B_3^2*Rtot^2 + 2*K_A_1^2*K_B_3*Ltot^2 - 4*K_A_1^2*K_B_3*Ltot*Rtot + 2*K_A_1^2*K_B_3*Rtot^2 + K_A_1^2*Ltot^2 - 2*K_A_1^2*Ltot*Rtot + K_A_1^2*Rtot^2 + 2*K_A_1*K_B_1*K_B_2*K_B_3*Ltot + 2*K_A_1*K_B_1*K_B_2*K_B_3*Rtot + 2*K_A_1*K_B_1*K_B_2*Ltot + 2*K_A_1*K_B_1*K_B_2*Rtot + 2*K_A_1*K_B_1*K_B_3*Ltot + 2*K_A_1*K_B_1*K_B_3*Rtot + 2*K_A_1*K_B_1*Ltot + 2*K_A_1*K_B_1*Rtot + 2*K_A_1*K_B_2*K_B_3*Ltot + 2*K_A_1*K_B_2*K_B_3*Rtot + 2*K_A_1*K_B_2*Ltot + 2*K_A_1*K_B_2*Rtot + 2*K_A_1*K_B_3*Ltot + 2*K_A_1*K_B_3*Rtot + 2*K_A_1*Ltot + 2*K_A_1*Rtot + K_B_1^2*K_B_2^2 + 2*K_B_1^2*K_B_2 + K_B_1^2 + 2*K_B_1*K_B_2^2 + 4*K_B_1*K_B_2 + 2*K_B_1 + K_B_2^2 + 2*K_B_2 + 1)^(1/2) + K_B_1*K_B_2 - K_A_1*Ltot + K_A_1*Rtot - K_A_1*K_B_3*Ltot + K_A_1*K_B_3*Rtot + 1)/(2*K_A_1*(K_B_2 + K_B_3 + K_B_2*K_B_3 + 1)) < Ltot or not (K_B_1 + K_B_2 + (K_A_1^2*K_B_3^2*Ltot^2 - 2*K_A_1^2*K_B_3^2*Ltot*Rtot + K_A_1^2*K_B_3^2*Rtot^2 + 2*K_A_1^2*K_B_3*Ltot^2 - 4*K_A_1^2*K_B_3*Ltot*Rtot + 2*K_A_1^2*K_B_3*Rtot^2 + K_A_1^2*Ltot^2 - 2*K_A_1^2*Ltot*Rtot + K_A_1^2*Rtot^2 + 2*K_A_1*K_B_1*K_B_2*K_B_3*Ltot + 2*K_A_1*K_B_1*K_B_2*K_B_3*Rtot + 2*K_A_1*K_B_1*K_B_2*Ltot + 2*K_A_1*K_B_1*K_B_2*Rtot + 2*K_A_1*K_B_1*K_B_3*Ltot + 2*K_A_1*K_B_1*K_B_3*Rtot + 2*K_A_1*K_B_1*Ltot + 2*K_A_1*K_B_1*Rtot + 2*K_A_1*K_B_2*K_B_3*Ltot + 2*K_A_1*K_B_2*K_B_3*Rtot + 2*K_A_1*K_B_2*Ltot + 2*K_A_1*K_B_2*Rtot + 2*K_A_1*K_B_3*Ltot + 2*K_A_1*K_B_3*Rtot + 2*K_A_1*Ltot + 2*K_A_1*Rtot + K_B_1^2*K_B_2^2 + 2*K_B_1^2*K_B_2 + K_B_1^2 + 2*K_B_1*K_B_2^2 + 4*K_B_1*K_B_2 + 2*K_B_1 + K_B_2^2 + 2*K_B_2 + 1)^(1/2) + K_B_1*K_B_2 - K_A_1*Ltot + K_A_1*Rtot - K_A_1*K_B_3*Ltot + K_A_1*K_B_3*Rtot + 1)/(K_B_2 + K_B_3 + K_B_2*K_B_3 + 1) < 0) and -(K_B_1 + K_B_2 - (K_A_1^2*K_B_3^2*Ltot^2 - 2*K_A_1^2*K_B_3^2*Ltot*Rtot + K_A_1^2*K_B_3^2*Rtot^2 + 2*K_A_1^2*K_B_3*Ltot^2 - 4*K_A_1^2*K_B_3*Ltot*Rtot + 2*K_A_1^2*K_B_3*Rtot^2 + K_A_1^2*Ltot^2 - 2*K_A_1^2*Ltot*Rtot + K_A_1^2*Rtot^2 + 2*K_A_1*K_B_1*K_B_2*K_B_3*Ltot + 2*K_A_1*K_B_1*K_B_2*K_B_3*Rtot + 2*K_A_1*K_B_1*K_B_2*Ltot + 2*K_A_1*K_B_1*K_B_2*Rtot + 2*K_A_1*K_B_1*K_B_3*Ltot + 2*K_A_1*K_B_1*K_B_3*Rtot + 2*K_A_1*K_B_1*Ltot + 2*K_A_1*K_B_1*Rtot + 2*K_A_1*K_B_2*K_B_3*Ltot + 2*K_A_1*K_B_2*K_B_3*Rtot + 2*K_A_1*K_B_2*Ltot + 2*K_A_1*K_B_2*Rtot + 2*K_A_1*K_B_3*Ltot + 2*K_A_1*K_B_3*Rtot + 2*K_A_1*Ltot + 2*K_A_1*Rtot + K_B_1^2*K_B_2^2 + 2*K_B_1^2*K_B_2 + K_B_1^2 + 2*K_B_1*K_B_2^2 + 4*K_B_1*K_B_2 + 2*K_B_1 + K_B_2^2 + 2*K_B_2 + 1)^(1/2) + K_B_1*K_B_2 - K_A_1*Ltot + K_A_1*Rtot - K_A_1*K_B_3*Ltot + K_A_1*K_B_3*Rtot + 1)/(2*K_A_1*(K_B_2 + K_B_3 + K_B_2*K_B_3 + 1)) < Ltot and (K_B_1 + K_B_2 - (K_A_1^2*K_B_3^2*Ltot^2 - 2*K_A_1^2*K_B_3^2*Ltot*Rtot + K_A_1^2*K_B_3^2*Rtot^2 + 2*K_A_1^2*K_B_3*Ltot^2 - 4*K_A_1^2*K_B_3*Ltot*Rtot + 2*K_A_1^2*K_B_3*Rtot^2 + K_A_1^2*Ltot^2 - 2*K_A_1^2*Ltot*Rtot + K_A_1^2*Rtot^2 + 2*K_A_1*K_B_1*K_B_2*K_B_3*Ltot + 2*K_A_1*K_B_1*K_B_2*K_B_3*Rtot + 2*K_A_1*K_B_1*K_B_2*Ltot + 2*K_A_1*K_B_1*K_B_2*Rtot + 2*K_A_1*K_B_1*K_B_3*Ltot + 2*K_A_1*K_B_1*K_B_3*Rtot + 2*K_A_1*K_B_1*Ltot + 2*K_A_1*K_B_1*Rtot + 2*K_A_1*K_B_2*K_B_3*Ltot + 2*K_A_1*K_B_2*K_B_3*Rtot + 2*K_A_1*K_B_2*Ltot + 2*K_A_1*K_B_2*Rtot + 2*K_A_1*K_B_3*Ltot + 2*K_A_1*K_B_3*Rtot + 2*K_A_1*Ltot + 2*K_A_1*Rtot + K_B_1^2*K_B_2^2 + 2*K_B_1^2*K_B_2 + K_B_1^2 + 2*K_B_1*K_B_2^2 + 4*K_B_1*K_B_2 + 2*K_B_1 + K_B_2^2 + 2*K_B_2 + 1)^(1/2) + K_B_1*K_B_2 - K_A_1*Ltot + K_A_1*Rtot - K_A_1*K_B_3*Ltot + K_A_1*K_B_3*Rtot + 1)/(K_B_2 + K_B_3 + K_B_2*K_B_3 + 1) < 0 and (K_A_1^2*K_B_3^2*Ltot^2 - 2*K_A_1^2*K_B_3^2*Ltot*Rtot + K_A_1^2*K_B_3^2*Rtot^2 + 2*K_A_1^2*K_B_3*Ltot^2 - 4*K_A_1^2*K_B_3*Ltot*Rtot + 2*K_A_1^2*K_B_3*Rtot^2 + K_A_1^2*Ltot^2 - 2*K_A_1^2*Ltot*Rtot + K_A_1^2*Rtot^2 + 2*K_A_1*K_B_1*K_B_2*K_B_3*Ltot + 2*K_A_1*K_B_1*K_B_2*K_B_3*Rtot + 2*K_A_1*K_B_1*K_B_2*Ltot + 2*K_A_1*K_B_1*K_B_2*Rtot + 2*K_A_1*K_B_1*K_B_3*Ltot + 2*K_A_1*K_B_1*K_B_3*Rtot + 2*K_A_1*K_B_1*Ltot + 2*K_A_1*K_B_1*Rtot + 2*K_A_1*K_B_2*K_B_3*Ltot + 2*K_A_1*K_B_2*K_B_3*Rtot + 2*K_A_1*K_B_2*Ltot + 2*K_A_1*K_B_2*Rtot + 2*K_A_1*K_B_3*Ltot + 2*K_A_1*K_B_3*Rtot + 2*K_A_1*Ltot + 2*K_A_1*Rtot + K_B_1^2*K_B_2^2 + 2*K_B_1^2*K_B_2 + K_B_1^2 + 2*K_B_1*K_B_2^2 + 4*K_B_1*K_B_2 + 2*K_B_1 + K_B_2^2 + 2*K_B_2 + 1)^(1/2) + K_A_1*Ltot + K_A_1*K_B_3*Ltot <> K_B_1 + K_B_2 + K_B_1*K_B_2 + K_A_1*Rtot + K_A_1*K_B_3*Rtot + 1 and K_B_1 + K_B_2 + (K_A_1^2*K_B_3^2*Ltot^2 - 2*K_A_1^2*K_B_3^2*Ltot*Rtot + K_A_1^2*K_B_3^2*Rtot^2 + 2*K_A_1^2*K_B_3*Ltot^2 - 4*K_A_1^2*K_B_3*Ltot*Rtot + 2*K_A_1^2*K_B_3*Rtot^2 + K_A_1^2*Ltot^2 - 2*K_A_1^2*Ltot*Rtot + K_A_1^2*Rtot^2 + 2*K_A_1*K_B_1*K_B_2*K_B_3*Ltot + 2*K_A_1*K_B_1*K_B_2*K_B_3*Rtot + 2*K_A_1*K_B_1*K_B_2*Ltot + 2*K_A_1*K_B_1*K_B_2*Rtot + 2*K_A_1*K_B_1*K_B_3*Ltot + 2*K_A_1*K_B_1*K_B_3*Rtot + 2*K_A_1*K_B_1*Ltot + 2*K_A_1*K_B_1*Rtot + 2*K_A_1*K_B_2*K_B_3*Ltot + 2*K_A_1*K_B_2*K_B_3*Rtot + 2*K_A_1*K_B_2*Ltot + 2*K_A_1*K_B_2*Rtot + 2*K_A_1*K_B_3*Ltot + 2*K_A_1*K_B_3*Rtot + 2*K_A_1*Ltot + 2*K_A_1*Rtot + K_B_1^2*K_B_2^2 + 2*K_B_1^2*K_B_2 + K_B_1^2 + 2*K_B_1*K_B_2^2 + 4*K_B_1*K_B_2 + 2*K_B_1 + K_B_2^2 + 2*K_B_2 + 1)^(1/2) + K_B_1*K_B_2 + K_A_1*Rtot + K_A_1*K_B_3*Rtot + 1 <> K_A_1*Ltot + K_A_1*K_B_3*Ltot or not -(K_B_1 + K_B_2 + (K_A_1^2*K_B_3^2*Ltot^2 - 2*K_A_1^2*K_B_3^2*Ltot*Rtot + K_A_1^2*K_B_3^2*Rtot^2 + 2*K_A_1^2*K_B_3*Ltot^2 - 4*K_A_1^2*K_B_3*Ltot*Rtot + 2*K_A_1^2*K_B_3*Rtot^2 + K_A_1^2*Ltot^2 - 2*K_A_1^2*Ltot*Rtot + K_A_1^2*Rtot^2 + 2*K_A_1*K_B_1*K_B_2*K_B_3*Ltot + 2*K_A_1*K_B_1*K_B_2*K_B_3*Rtot + 2*K_A_1*K_B_1*K_B_2*Ltot + 2*K_A_1*K_B_1*K_B_2*Rtot + 2*K_A_1*K_B_1*K_B_3*Ltot + 2*K_A_1*K_B_1*K_B_3*Rtot + 2*K_A_1*K_B_1*Ltot + 2*K_A_1*K_B_1*Rtot + 2*K_A_1*K_B_2*K_B_3*Ltot + 2*K_A_1*K_B_2*K_B_3*Rtot + 2*K_A_1*K_B_2*Ltot + 2*K_A_1*K_B_2*Rtot + 2*K_A_1*K_B_3*Ltot + 2*K_A_1*K_B_3*Rtot + 2*K_A_1*Ltot + 2*K_A_1*Rtot + K_B_1^2*K_B_2^2 + 2*K_B_1^2*K_B_2 + K_B_1^2 + 2*K_B_1*K_B_2^2 + 4*K_B_1*K_B_2 + 2*K_B_1 + K_B_2^2 + 2*K_B_2 + 1)^(1/2) + K_B_1*K_B_2 - K_A_1*Ltot + K_A_1*Rtot - K_A_1*K_B_3*Ltot + K_A_1*K_B_3*Rtot + 1)/(2*K_A_1*(K_B_2 + K_B_3 + K_B_2*K_B_3 + 1)) < Ltot and (K_B_1 + K_B_2 + (K_A_1^2*K_B_3^2*Ltot^2 - 2*K_A_1^2*K_B_3^2*Ltot*Rtot + K_A_1^2*K_B_3^2*Rtot^2 + 2*K_A_1^2*K_B_3*Ltot^2 - 4*K_A_1^2*K_B_3*Ltot*Rtot + 2*K_A_1^2*K_B_3*Rtot^2 + K_A_1^2*Ltot^2 - 2*K_A_1^2*Ltot*Rtot + K_A_1^2*Rtot^2 + 2*K_A_1*K_B_1*K_B_2*K_B_3*Ltot + 2*K_A_1*K_B_1*K_B_2*K_B_3*Rtot + 2*K_A_1*K_B_1*K_B_2*Ltot + 2*K_A_1*K_B_1*K_B_2*Rtot + 2*K_A_1*K_B_1*K_B_3*Ltot + 2*K_A_1*K_B_1*K_B_3*Rtot + 2*K_A_1*K_B_1*Ltot + 2*K_A_1*K_B_1*Rtot + 2*K_A_1*K_B_2*K_B_3*Ltot + 2*K_A_1*K_B_2*K_B_3*Rtot + 2*K_A_1*K_B_2*Ltot + 2*K_A_1*K_B_2*Rtot + 2*K_A_1*K_B_3*Ltot + 2*K_A_1*K_B_3*Rtot + 2*K_A_1*Ltot + 2*K_A_1*Rtot + K_B_1^2*K_B_2^2 + 2*K_B_1^2*K_B_2 + K_B_1^2 + 2*K_B_1*K_B_2^2 + 4*K_B_1*K_B_2 + 2*K_B_1 + K_B_2^2 + 2*K_B_2 + 1)^(1/2) + K_B_1*K_B_2 - K_A_1*Ltot + K_A_1*Rtot - K_A_1*K_B_3*Ltot + K_A_1*K_B_3*Rtot + 1)/(K_B_2 + K_B_3 + K_B_2*K_B_3 + 1) < 0 and not -(K_B_1 + K_B_2 - (K_A_1^2*K_B_3^2*Ltot^2 - 2*K_A_1^2*K_B_3^2*Ltot*Rtot + K_A_1^2*K_B_3^2*Rtot^2 + 2*K_A_1^2*K_B_3*Ltot^2 - 4*K_A_1^2*K_B_3*Ltot*Rtot + 2*K_A_1^2*K_B_3*Rtot^2 + K_A_1^2*Ltot^2 - 2*K_A_1^2*Ltot*Rtot + K_A_1^2*Rtot^2 + 2*K_A_1*K_B_1*K_B_2*K_B_3*Ltot + 2*K_A_1*K_B_1*K_B_2*K_B_3*Rtot + 2*K_A_1*K_B_1*K_B_2*Ltot + 2*K_A_1*K_B_1*K_B_2*Rtot + 2*K_A_1*K_B_1*K_B_3*Ltot + 2*K_A_1*K_B_1*K_B_3*Rtot + 2*K_A_1*K_B_1*Ltot + 2*K_A_1*K_B_1*Rtot + 2*K_A_1*K_B_2*K_B_3*Ltot + 2*K_A_1*K_B_2*K_B_3*Rtot + 2*K_A_1*K_B_2*Ltot + 2*K_A_1*K_B_2*Rtot + 2*K_A_1*K_B_3*Ltot + 2*K_A_1*K_B_3*Rtot + 2*K_A_1*Ltot + 2*K_A_1*Rtot + K_B_1^2*K_B_2^2 + 2*K_B_1^2*K_B_2 + K_B_1^2 + 2*K_B_1*K_B_2^2 + 4*K_B_1*K_B_2 + 2*K_B_1 + K_B_2^2 + 2*K_B_2 + 1)^(1/2) + K_B_1*K_B_2 - K_A_1*Ltot + K_A_1*Rtot - K_A_1*K_B_3*Ltot + K_A_1*K_B_3*Rtot + 1)/(2*K_A_1*(K_B_2 + K_B_3 + K_B_2*K_B_3 + 1)) < Ltot and (K_B_1 + K_B_2 - (K_A_1^2*K_B_3^2*Ltot^2 - 2*K_A_1^2*K_B_3^2*Ltot*Rtot + K_A_1^2*K_B_3^2*Rtot^2 + 2*K_A_1^2*K_B_3*Ltot^2 - 4*K_A_1^2*K_B_3*Ltot*Rtot + 2*K_A_1^2*K_B_3*Rtot^2 + K_A_1^2*Ltot^2 - 2*K_A_1^2*Ltot*Rtot + K_A_1^2*Rtot^2 + 2*K_A_1*K_B_1*K_B_2*K_B_3*Ltot + 2*K_A_1*K_B_1*K_B_2*K_B_3*Rtot + 2*K_A_1*K_B_1*K_B_2*Ltot + 2*K_A_1*K_B_1*K_B_2*Rtot + 2*K_A_1*K_B_1*K_B_3*Ltot + 2*K_A_1*K_B_1*K_B_3*Rtot + 2*K_A_1*K_B_1*Ltot + 2*K_A_1*K_B_1*Rtot + 2*K_A_1*K_B_2*K_B_3*Ltot + 2*K_A_1*K_B_2*K_B_3*Rtot + 2*K_A_1*K_B_2*Ltot + 2*K_A_1*K_B_2*Rtot + 2*K_A_1*K_B_3*Ltot + 2*K_A_1*K_B_3*Rtot + 2*K_A_1*Ltot + 2*K_A_1*Rtot + K_B_1^2*K_B_2^2 + 2*K_B_1^2*K_B_2 + K_B_1^2 + 2*K_B_1*K_B_2^2 + 4*K_B_1*K_B_2 + 2*K_B_1 + K_B_2^2 + 2*K_B_2 + 1)^(1/2) + K_B_1*K_B_2 - K_A_1*Ltot + K_A_1*Rtot - K_A_1*K_B_3*Ltot + K_A_1*K_B_3*Rtot + 1)/(K_B_2 + K_B_3 + K_B_2*K_B_3 + 1) < 0 and (K_A_1^2*K_B_3^2*Ltot^2 - 2*K_A_1^2*K_B_3^2*Ltot*Rtot + K_A_1^2*K_B_3^2*Rtot^2 + 2*K_A_1^2*K_B_3*Ltot^2 - 4*K_A_1^2*K_B_3*Ltot*Rtot + 2*K_A_1^2*K_B_3*Rtot^2 + K_A_1^2*Ltot^2 - 2*K_A_1^2*Ltot*Rtot + K_A_1^2*Rtot^2 + 2*K_A_1*K_B_1*K_B_2*K_B_3*Ltot + 2*K_A_1*K_B_1*K_B_2*K_B_3*Rtot + 2*K_A_1*K_B_1*K_B_2*Ltot + 2*K_A_1*K_B_1*K_B_2*Rtot + 2*K_A_1*K_B_1*K_B_3*Ltot + 2*K_A_1*K_B_1*K_B_3*Rtot + 2*K_A_1*K_B_1*Ltot + 2*K_A_1*K_B_1*Rtot + 2*K_A_1*K_B_2*K_B_3*Ltot + 2*K_A_1*K_B_2*K_B_3*Rtot + 2*K_A_1*K_B_2*Ltot + 2*K_A_1*K_B_2*Rtot + 2*K_A_1*K_B_3*Ltot + 2*K_A_1*K_B_3*Rtot + 2*K_A_1*Ltot + 2*K_A_1*Rtot + K_B_1^2*K_B_2^2 + 2*K_B_1^2*K_B_2 + K_B_1^2 + 2*K_B_1*K_B_2^2 + 4*K_B_1*K_B_2 + 2*K_B_1 + K_B_2^2 + 2*K_B_2 + 1)^(1/2) + K_A_1*Ltot + K_A_1*K_B_3*Ltot <> K_B_1 + K_B_2 + K_B_1*K_B_2 + K_A_1*Rtot + K_A_1*K_B_3*Rtot + 1 and K_B_1 + K_B_2 + (K_A_1^2*K_B_3^2*Ltot^2 - 2*K_A_1^2*K_B_3^2*Ltot*Rtot + K_A_1^2*K_B_3^2*Rtot^2 + 2*K_A_1^2*K_B_3*Ltot^2 - 4*K_A_1^2*K_B_3*Ltot*Rtot + 2*K_A_1^2*K_B_3*Rtot^2 + K_A_1^2*Ltot^2 - 2*K_A_1^2*Ltot*Rtot + K_A_1^2*Rtot^2 + 2*K_A_1*K_B_1*K_B_2*K_B_3*Ltot + 2*K_A_1*K_B_1*K_B_2*K_B_3*Rtot + 2*K_A_1*K_B_1*K_B_2*Ltot + 2*K_A_1*K_B_1*K_B_2*Rtot + 2*K_A_1*K_B_1*K_B_3*Ltot + 2*K_A_1*K_B_1*K_B_3*Rtot + 2*K_A_1*K_B_1*Ltot + 2*K_A_1*K_B_1*Rtot + 2*K_A_1*K_B_2*K_B_3*Ltot + 2*K_A_1*K_B_2*K_B_3*Rtot + 2*K_A_1*K_B_2*Ltot + 2*K_A_1*K_B_2*Rtot + 2*K_A_1*K_B_3*Ltot + 2*K_A_1*K_B_3*Rtot + 2*K_A_1*Ltot + 2*K_A_1*Rtot + K_B_1^2*K_B_2^2 + 2*K_B_1^2*K_B_2 + K_B_1^2 + 2*K_B_1*K_B_2^2 + 4*K_B_1*K_B_2 + 2*K_B_1 + K_B_2^2 + 2*K_B_2 + 1)^(1/2) + K_B_1*K_B_2 + K_A_1*Rtot + K_A_1*K_B_3*Rtot + 1 <> K_A_1*Ltot + K_A_1*K_B_3*Ltot or K_A_1^2*K_B_3^2*Ltot^2 + K_A_1^2*K_B_3^2*Rtot^2 + 2*K_A_1^2*K_B_3*Ltot^2 + 2*K_A_1^2*K_B_3*Rtot^2 + K_A_1^2*Ltot^2 + K_A_1^2*Rtot^2 + 2*K_A_1*K_B_1*K_B_2*K_B_3*Ltot + 2*K_A_1*K_B_1*K_B_2*K_B_3*Rtot + 2*K_A_1*K_B_1*K_B_2*Ltot + 2*K_A_1*K_B_1*K_B_2*Rtot + 2*K_A_1*K_B_1*K_B_3*Ltot + 2*K_A_1*K_B_1*K_B_3*Rtot + 2*K_A_1*K_B_1*Ltot + 2*K_A_1*K_B_1*Rtot + 2*K_A_1*K_B_2*K_B_3*Ltot + 2*K_A_1*K_B_2*K_B_3*Rtot + 2*K_A_1*K_B_2*Ltot + 2*K_A_1*K_B_2*Rtot + 2*K_A_1*K_B_3*Ltot + 2*K_A_1*K_B_3*Rtot + 2*K_A_1*Ltot + 2*K_A_1*Rtot + K_B_1^2*K_B_2^2 + 2*K_B_1^2*K_B_2 + K_B_1^2 + 2*K_B_1*K_B_2^2 + 4*K_B_1*K_B_2 + 2*K_B_1 + K_B_2^2 + 2*K_B_2 + 1 < 2*Ltot*Rtot*K_A_1^2*K_B_3^2 + 4*Ltot*Rtot*K_A_1^2*K_B_3 + 2*Ltot*Rtot*K_A_1^2 and -(K_B_1 + K_B_2 + (K_A_1^2*K_B_3^2*Ltot^2 - 2*K_A_1^2*K_B_3^2*Ltot*Rtot + K_A_1^2*K_B_3^2*Rtot^2 + 2*K_A_1^2*K_B_3*Ltot^2 - 4*K_A_1^2*K_B_3*Ltot*Rtot + 2*K_A_1^2*K_B_3*Rtot^2 + K_A_1^2*Ltot^2 - 2*K_A_1^2*Ltot*Rtot + K_A_1^2*Rtot^2 + 2*K_A_1*K_B_1*K_B_2*K_B_3*Ltot + 2*K_A_1*K_B_1*K_B_2*K_B_3*Rtot + 2*K_A_1*K_B_1*K_B_2*Ltot + 2*K_A_1*K_B_1*K_B_2*Rtot + 2*K_A_1*K_B_1*K_B_3*Ltot + 2*K_A_1*K_B_1*K_B_3*Rtot + 2*K_A_1*K_B_1*Ltot + 2*K_A_1*K_B_1*Rtot + 2*K_A_1*K_B_2*K_B_3*Ltot + 2*K_A_1*K_B_2*K_B_3*Rtot + 2*K_A_1*K_B_2*Ltot + 2*K_A_1*K_B_2*Rtot + 2*K_A_1*K_B_3*Ltot + 2*K_A_1*K_B_3*Rtot + 2*K_A_1*Ltot + 2*K_A_1*Rtot + K_B_1^2*K_B_2^2 + 2*K_B_1^2*K_B_2 + K_B_1^2 + 2*K_B_1*K_B_2^2 + 4*K_B_1*K_B_2 + 2*K_B_1 + K_B_2^2 + 2*K_B_2 + 1)^(1/2) + K_B_1*K_B_2 - K_A_1*Ltot + K_A_1*Rtot - K_A_1*K_B_3*Ltot + K_A_1*K_B_3*Rtot + 1)/(2*K_A_1*(K_B_2 + K_B_3 + K_B_2*K_B_3 + 1)) < Ltot and (K_B_1 + K_B_2 + (K_A_1^2*K_B_3^2*Ltot^2 - 2*K_A_1^2*K_B_3^2*Ltot*Rtot + K_A_1^2*K_B_3^2*Rtot^2 + 2*K_A_1^2*K_B_3*Ltot^2 - 4*K_A_1^2*K_B_3*Ltot*Rtot + 2*K_A_1^2*K_B_3*Rtot^2 + K_A_1^2*Ltot^2 - 2*K_A_1^2*Ltot*Rtot + K_A_1^2*Rtot^2 + 2*K_A_1*K_B_1*K_B_2*K_B_3*Ltot + 2*K_A_1*K_B_1*K_B_2*K_B_3*Rtot + 2*K_A_1*K_B_1*K_B_2*Ltot + 2*K_A_1*K_B_1*K_B_2*Rtot + 2*K_A_1*K_B_1*K_B_3*Ltot + 2*K_A_1*K_B_1*K_B_3*Rtot + 2*K_A_1*K_B_1*Ltot + 2*K_A_1*K_B_1*Rtot + 2*K_A_1*K_B_2*K_B_3*Ltot + 2*K_A_1*K_B_2*K_B_3*Rtot + 2*K_A_1*K_B_2*Ltot + 2*K_A_1*K_B_2*Rtot + 2*K_A_1*K_B_3*Ltot + 2*K_A_1*K_B_3*Rtot + 2*K_A_1*Ltot + 2*K_A_1*Rtot + K_B_1^2*K_B_2^2 + 2*K_B_1^2*K_B_2 + K_B_1^2 + 2*K_B_1*K_B_2^2 + 4*K_B_1*K_B_2 + 2*K_B_1 + K_B_2^2 + 2*K_B_2 + 1)^(1/2) + K_B_1*K_B_2 - K_A_1*Ltot + K_A_1*Rtot - K_A_1*K_B_3*Ltot + K_A_1*K_B_3*Rtot + 1)/(K_B_2 + K_B_3 + K_B_2*K_B_3 + 1) < 0 and -(K_B_1 + K_B_2 - (K_A_1^2*K_B_3^2*Ltot^2 - 2*K_A_1^2*K_B_3^2*Ltot*Rtot + K_A_1^2*K_B_3^2*Rtot^2 + 2*K_A_1^2*K_B_3*Ltot^2 - 4*K_A_1^2*K_B_3*Ltot*Rtot + 2*K_A_1^2*K_B_3*Rtot^2 + K_A_1^2*Ltot^2 - 2*K_A_1^2*Ltot*Rtot + K_A_1^2*Rtot^2 + 2*K_A_1*K_B_1*K_B_2*K_B_3*Ltot + 2*K_A_1*K_B_1*K_B_2*K_B_3*Rtot + 2*K_A_1*K_B_1*K_B_2*Ltot + 2*K_A_1*K_B_1*K_B_2*Rtot + 2*K_A_1*K_B_1*K_B_3*Ltot + 2*K_A_1*K_B_1*K_B_3*Rtot + 2*K_A_1*K_B_1*Ltot + 2*K_A_1*K_B_1*Rtot + 2*K_A_1*K_B_2*K_B_3*Ltot + 2*K_A_1*K_B_2*K_B_3*Rtot + 2*K_A_1*K_B_2*Ltot + 2*K_A_1*K_B_2*Rtot + 2*K_A_1*K_B_3*Ltot + 2*K_A_1*K_B_3*Rtot + 2*K_A_1*Ltot + 2*K_A_1*Rtot + K_B_1^2*K_B_2^2 + 2*K_B_1^2*K_B_2 + K_B_1^2 + 2*K_B_1*K_B_2^2 + 4*K_B_1*K_B_2 + 2*K_B_1 + K_B_2^2 + 2*K_B_2 + 1)^(1/2) + K_B_1*K_B_2 - K_A_1*Ltot + K_A_1*Rtot - K_A_1*K_B_3*Ltot + K_A_1*K_B_3*Rtot + 1)/(2*K_A_1*(K_B_2 + K_B_3 + K_B_2*K_B_3 + 1)) < Ltot and (K_B_1 + K_B_2 - (K_A_1^2*K_B_3^2*Ltot^2 - 2*K_A_1^2*K_B_3^2*Ltot*Rtot + K_A_1^2*K_B_3^2*Rtot^2 + 2*K_A_1^2*K_B_3*Ltot^2 - 4*K_A_1^2*K_B_3*Ltot*Rtot + 2*K_A_1^2*K_B_3*Rtot^2 + K_A_1^2*Ltot^2 - 2*K_A_1^2*Ltot*Rtot + K_A_1^2*Rtot^2 + 2*K_A_1*K_B_1*K_B_2*K_B_3*Ltot + 2*K_A_1*K_B_1*K_B_2*K_B_3*Rtot + 2*K_A_1*K_B_1*K_B_2*Ltot + 2*K_A_1*K_B_1*K_B_2*Rtot + 2*K_A_1*K_B_1*K_B_3*Ltot + 2*K_A_1*K_B_1*K_B_3*Rtot + 2*K_A_1*K_B_1*Ltot + 2*K_A_1*K_B_1*Rtot + 2*K_A_1*K_B_2*K_B_3*Ltot + 2*K_A_1*K_B_2*K_B_3*Rtot + 2*K_A_1*K_B_2*Ltot + 2*K_A_1*K_B_2*Rtot + 2*K_A_1*K_B_3*Ltot + 2*K_A_1*K_B_3*Rtot + 2*K_A_1*Ltot + 2*K_A_1*Rtot + K_B_1^2*K_B_2^2 + 2*K_B_1^2*K_B_2 + K_B_1^2 + 2*K_B_1*K_B_2^2 + 4*K_B_1*K_B_2 + 2*K_B_1 + K_B_2^2 + 2*K_B_2 + 1)^(1/2) + K_B_1*K_B_2 - K_A_1*Ltot + K_A_1*Rtot - K_A_1*K_B_3*Ltot + K_A_1*K_B_3*Rtot + 1)/(K_B_2 + K_B_3 + K_B_2*K_B_3 + 1) < 0 and (K_A_1^2*K_B_3^2*Ltot^2 - 2*K_A_1^2*K_B_3^2*Ltot*Rtot + K_A_1^2*K_B_3^2*Rtot^2 + 2*K_A_1^2*K_B_3*Ltot^2 - 4*K_A_1^2*K_B_3*Ltot*Rtot + 2*K_A_1^2*K_B_3*Rtot^2 + K_A_1^2*Ltot^2 - 2*K_A_1^2*Ltot*Rtot + K_A_1^2*Rtot^2 + 2*K_A_1*K_B_1*K_B_2*K_B_3*Ltot + 2*K_A_1*K_B_1*K_B_2*K_B_3*Rtot + 2*K_A_1*K_B_1*K_B_2*Ltot + 2*K_A_1*K_B_1*K_B_2*Rtot + 2*K_A_1*K_B_1*K_B_3*Ltot + 2*K_A_1*K_B_1*K_B_3*Rtot + 2*K_A_1*K_B_1*Ltot + 2*K_A_1*K_B_1*Rtot + 2*K_A_1*K_B_2*K_B_3*Ltot + 2*K_A_1*K_B_2*K_B_3*Rtot + 2*K_A_1*K_B_2*Ltot + 2*K_A_1*K_B_2*Rtot + 2*K_A_1*K_B_3*Ltot + 2*K_A_1*K_B_3*Rtot + 2*K_A_1*Ltot + 2*K_A_1*Rtot + K_B_1^2*K_B_2^2 + 2*K_B_1^2*K_B_2 + K_B_1^2 + 2*K_B_1*K_B_2^2 + 4*K_B_1*K_B_2 + 2*K_B_1 + K_B_2^2 + 2*K_B_2 + 1)^(1/2) + K_A_1*Ltot + K_A_1*K_B_3*Ltot <> K_B_1 + K_B_2 + K_B_1*K_B_2 + K_A_1*Rtot + K_A_1*K_B_3*Rtot + 1 and K_B_1 + K_B_2 + (K_A_1^2*K_B_3^2*Ltot^2 - 2*K_A_1^2*K_B_3^2*Ltot*Rtot + K_A_1^2*K_B_3^2*Rtot^2 + 2*K_A_1^2*K_B_3*Ltot^2 - 4*K_A_1^2*K_B_3*Ltot*Rtot + 2*K_A_1^2*K_B_3*Rtot^2 + K_A_1^2*Ltot^2 - 2*K_A_1^2*Ltot*Rtot + K_A_1^2*Rtot^2 + 2*K_A_1*K_B_1*K_B_2*K_B_3*Ltot + 2*K_A_1*K_B_1*K_B_2*K_B_3*Rtot + 2*K_A_1*K_B_1*K_B_2*Ltot + 2*K_A_1*K_B_1*K_B_2*Rtot + 2*K_A_1*K_B_1*K_B_3*Ltot + 2*K_A_1*K_B_1*K_B_3*Rtot + 2*K_A_1*K_B_1*Ltot + 2*K_A_1*K_B_1*Rtot + 2*K_A_1*K_B_2*K_B_3*Ltot + 2*K_A_1*K_B_2*K_B_3*Rtot + 2*K_A_1*K_B_2*Ltot + 2*K_A_1*K_B_2*Rtot + 2*K_A_1*K_B_3*Ltot + 2*K_A_1*K_B_3*Rtot + 2*K_A_1*Ltot + 2*K_A_1*Rtot + K_B_1^2*K_B_2^2 + 2*K_B_1^2*K_B_2 + K_B_1^2 + 2*K_B_1*K_B_2^2 + 4*K_B_1*K_B_2 + 2*K_B_1 + K_B_2^2 + 2*K_B_2 + 1)^(1/2) + K_B_1*K_B_2 + K_A_1*Rtot + K_A_1*K_B_3*Rtot + 1 <> K_A_1*Ltot + K_A_1*K_B_3*Ltot, {}])](U-R-L-RL_derivation_images/math50.png)
Extract solutions
solution_lines:=4:
eq3_13:= solution3_12[i,1] $ i=1..solution_lines;
nops(%)

![]()
Is 1st solution a combination of 2nd and 3rd?
solution1:=eq3_13[1]; // a sequence of roots
solution2:=eq3_13[2][1]; // extract equation out of a sequence
solution3:=eq3_13[3][1]; // extract equation out of a sequence
if solution2 in solution1
then print(Unquoted,"First set of roots contains the second root.");
else print(Unquoted,"First set of roots DOES NOT contain the second root!");
end_if;
if solution3 in solution1
then print(Unquoted,"First set of roots contains the third root.");
else print(Unquoted,"First set of roots DOES NOT contain the third root!");
end_if;



First set of roots DOES NOT contain the second root!
First set of roots DOES NOT contain the third root!
Check correctness of the solution by substitution
// Check the 2nd root
test1:=eq3_12 | Leq=solution2;
normal(%);


good
// Check the 3rd root
test1:=eq3_12 | Leq=solution3;
normal(%);


good
=> BOTH SOLUTIONS ARE CORRECT.
Test which solution is meaningful
solution2 | K_A_1=1 | K_B_1=1 | K_B_2=1 | K_B_3=1 | Rtot=1 | Ltot=1;
float(%)
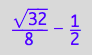
![]()
meaningless
solution3 | K_A_1=1 | K_B_1=1 | K_B_2=1 | K_B_3=1 | Rtot=1 | Ltot=1;
float(%)
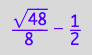
![]()
=> MEANINGFUL
Choose as a final solution
eq3_14:= Leq = solution3

Summary of equations for all species
Leq_U_R_L_RL:=eq3_14

Req_U_R_L_RL:=eq3_11

Rstareq_U_R_L_RL:=eq3_7
![]()
Lstareq_U_R_L_RL:=eq3_9
![]()
RLeq_U_R_L_RL:=eq3_4
![]()
RLstareq_U_R_L_RL:=eq3_1
![]()
Create functions for computing concentrations
Here I only check that the results are numerically meaningful--functions were created right. Scientific meaningfulness will be analyzed in a separate notebook 'Analysis'.
(use --> to force direct substitution):
fLeq_U_R_L_RL:= (Rtot, Ltot, K_A_1, K_B_1, K_B_2, K_B_3) --> Leq_U_R_L_RL[2]

//test operation
fLeq_U_R_L_RL(1,1,10,100,1000,1):
float(%)
![]()
=> OK
fReq_U_R_L_RL:=(Rtot, Ltot, K_A_1, K_B_1, K_B_2, K_B_3) --> Req_U_R_L_RL[2] | Leq_U_R_L_RL

//test operation
fReq_U_R_L_RL(1,1,10,100,1000,1):
float(%)
![]()
=> OK
fRstareq_U_R_L_RL:=(Rtot, Ltot, K_A_1, K_B_1, K_B_2, K_B_3) --> Rstareq_U_R_L_RL[2] | Req_U_R_L_RL | Leq_U_R_L_RL

//test operation
fRstareq_U_R_L_RL(1,1,10,100,1000,1):
float(%)
![]()
=> OK
fLstareq_U_R_L_RL:=(Rtot, Ltot, K_A_1, K_B_1, K_B_2, K_B_3) --> Lstareq_U_R_L_RL[2] | Leq_U_R_L_RL

//test operation
fLstareq_U_R_L_RL(1,1,10,100,1000,1):
float(%)
![]()
=> OK
fRLeq_U_R_L_RL:=(Rtot, Ltot, K_A_1, K_B_1, K_B_2, K_B_3) --> RLeq_U_R_L_RL[2] | Req_U_R_L_RL | Leq_U_R_L_RL

//test operation
fRLeq_U_R_L_RL(1,1,10,100,1000,1):
float(%)
![]()
=> OK
fRLstareq_U_R_L_RL:=(Rtot, Ltot, K_A_1, K_B_1, K_B_2, K_B_3) --> RLstareq_U_R_L_RL[2] | RLeq_U_R_L_RL | Req_U_R_L_RL | Leq_U_R_L_RL

//test operation
fRLstareq_U_R_L_RL(1,1,10,100,1000,1):
float(%)
![]()
=> OK
(you can retrieve them later by executing: fread(filename,Quiet))
ProjectName
![]()
filename:=CurrentPath.ProjectName.".mb";
write(filename,
// Equations
Leq_U_R_L_RL,
Req_U_R_L_RL,
Rstareq_U_R_L_RL,
Lstareq_U_R_L_RL,
RLeq_U_R_L_RL,
RLstareq_U_R_L_RL,
// Analytical functions
fLeq_U_R_L_RL,
fReq_U_R_L_RL,
fRstareq_U_R_L_RL,
fLstareq_U_R_L_RL,
fRLeq_U_R_L_RL,
fRLstareq_U_R_L_RL
)

Error: Cannot write to file '/Users/kovrigin/Documents/Workspace/Global Analysis/code_development/Mathematical_models/Equilibrium_thermodynamic_models/U-R-L-RL/U-R-L-RL.mb'. [write]
Conclusions
1. Analytical solution obtained.
2. Functions for analysis of behavior of solutions are created and saved.