U_R_L_derivation

Derivation of equations for U-R-L model

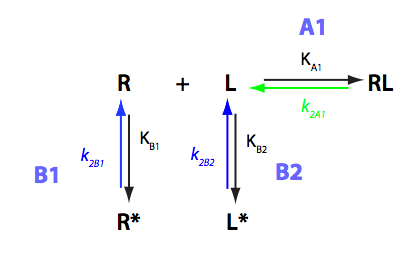
Binding coupled with intramolecular isomerization of both receptor and a ligand into unbinding conformations

2. Derivation of a main equation

3. Define functions for equilibrium concentrations

6. Save results on disk for future use

Back to Contents

In this notebook I will derive analytical solutions for U-R-L model and prepare equations for numerical simulations.

Back to Contents

clean up workspace

reset()

Set path to save results into:

ProjectName:="U_R_L";

CurrentPath:="/Users/kovrigin/Documents/Workspace/Data/Data.XV/EKM16.Analysis_of_multistep_kinetic_mechanisms/Equilibria/U_R_L_model/";

Binding and isomerization constants

All binding constants I am using are association constants.

These relationships serve as restraints for solve(), but not restrict these values in calculations!

K_A_1

K_A_1 ;

assumeAlso(K_A_1 > 0):

assumeAlso(K_A_1 , R_):

Isomerization constants are formation constants for the alternative species

K_B_1

K_B_1 ;

assumeAlso(K_B_1 > 0):

assumeAlso(K_B_1 , R_):

K_B_2

K_B_2 ;

assumeAlso(K_B_2 > 0):

assumeAlso(K_B_2 , R_):

Total concentrations

Rtot - total concentration of the receptor

Rtot;

assumeAlso(Rtot>0):

assumeAlso(Rtot,R_):

Ltot - total concentration of a ligand

Ltot;

assumeAlso(Ltot>0):

assumeAlso(Ltot,R_):

Common equilibrium concentrations

Req - equilibrium concentration of a receptor monomer

Req;

assumeAlso(Req>0):

assumeAlso(Req<Rtot):

assumeAlso(Req,R_):

Rstareq - equilibrium concentration of an nonbinding receptor isomer

Rstareq;

assumeAlso(Rstareq>0):

assumeAlso(Rstareq<Rtot):

assumeAlso(Rstareq,R_):

Leq - equilibrium concentration of a free ligand

Leq;

assumeAlso(Leq>0):

assumeAlso(Leq<Ltot):

assumeAlso(Leq,R_):

Lstareq - equilibrium concentration of a nonbinding ligand isomer

Lstareq;

assumeAlso(Lstareq>0):

assumeAlso(Lstareq<Ltot):

assumeAlso(Lstareq,R_):

RLeq - equilibrium concentration of a receptor-ligand complex

RLeq;

assumeAlso(RLeq>0):

assumeAlso(RLeq<Rtot):

assumeAlso(RLeq,R_):

anames(Properties,User);

math

Back to Contents

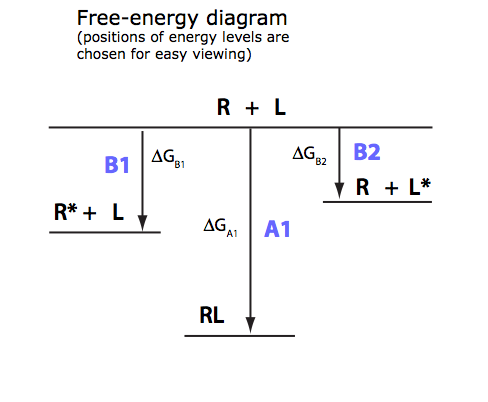
2. Derivation of a main equation

Working equation: I will try to express analytical [L] from equation for a total concentration of a receptor or use the expression for a numeric solution if analytical is not possible

eq2_1:= Rtot= Req + Rstareq + RLeq;

eq2_2:= Ltot= Leq + Lstareq + RLeq;

Equilbrium thermodynamic equations:

eq2_3:= K_A_1 = RLeq/(Req*Leq)

math

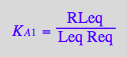
eq2_4:= K_B_1 = Rstareq/Req

math

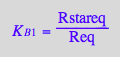
eq2_5:= K_B_2 = Lstareq/Leq

math

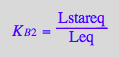
Express all species in terms of Req and Leq

Lstareq

eq2_5;

solve(%, Lstareq);

%[1][1];

eq2_6:= Lstareq = %

math

math

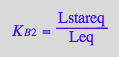
Rstareq

eq2_4;

solve(%,Rstareq);

%[1][1];

eq2_7:= Rstareq = %

math

math

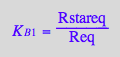
RLeq

eq2_3;

solve(%,RLeq);

%[1][1];

eq2_8:= RLeq = %

math

math

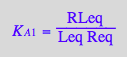
Substitute into mass action laws

express Req

eq2_2;

% | eq2_6 | eq2_8;

solve(%,Req);

%[1][1];

eq2_9:= Req = %

math

math

math

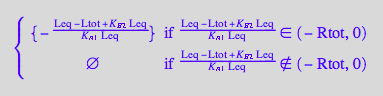
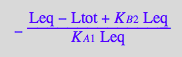
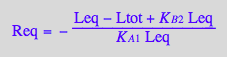
eq2_1;

% | eq2_8 | eq2_7 | eq2_9 ;

eq2_10:= %:

math

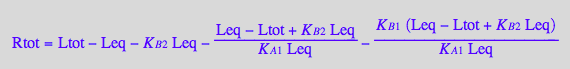
Solve for Leq

solutions2_10:=solve(eq2_10,Leq)

math

Extract solutions

eq2_11:= solutions2_10[i,1] $ i=1..nops(solutions2_10);

nops(%)

math

Is the 1st solution a combination of 2nd and 3rd?

solution1:=eq2_11[1]; // a sequence of roots

solution2:=eq2_11[2][1]; // extract equation out of a sequence

solution3:=eq2_11[3][1]; // extract equation out of a sequence

if solution2 in solution1

then print(Unquoted,"First set of roots contains the second root.");

else print(Unquoted,"First set of roots DOES NOT contain the second root!");

end_if;

if solution3 in solution1

then print(Unquoted,"First set of roots contains the third root.");

else print(Unquoted,"First set of roots DOES NOT contain the third root!");

end_if;

math

math

math

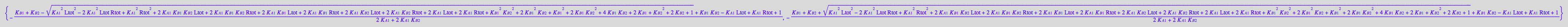
First set of roots contains the second root.

First set of roots contains the third root.

Check correctness of the solutions by substitution into original equation solved:

Check the first root

test1:= eq2_10 | Leq=solution2:

normal(%);

Check the second root

test1:= eq2_10 | Leq=solution3:

normal(%);

Both solutions are correct.

Select meaningful solution by substituting parameters

solution2 | K_A_1=1 | K_B_1=1 | K_B_2=1 | Ltot=1 | Rtot =1;

float(%);

math

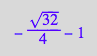
Not meaningful.

solution3 | K_A_1=1 | K_B_1=1 | K_B_2=1 | Ltot=1 | Rtot =1;

float(%);

math

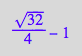
Solution 3 is meaningful!

Assign it to an equation

eq2_12:= Leq = solution3

math

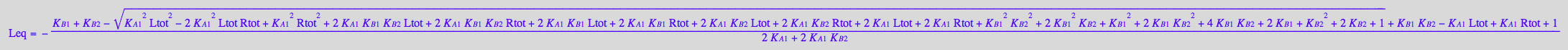
Derive apparent constant value

If only total unbound R and total unbound L is measured what is the apparent binding constant?

eq2_13:= R_U=Req+Rstareq;

eq2_14:= L_U=Leq+Lstareq;

Apparent binding constant in terms of 'unbound species'

eq2_15:= Kapp= RLeq/(R_U*L_U);

math

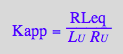
Express in terms of microscopic species:

eq2_16:= eq2_15 | eq2_13 | eq2_14

math

Express in terms of true constants

eq2_16 | eq2_6 | eq2_7 | eq2_8;

normal(%);

eq2_17:=%;

math

math

math

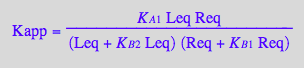
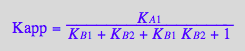
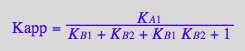
Factor the denominator

op(eq2_17,[2,2,1]);

factor(%);

eq2_18:= %

math

math

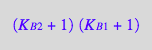
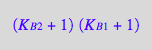
Reassemble the equation

op(eq2_17,[1]) = op(eq2_17,[2,1])/eq2_18;

eq2_19:= %:

math

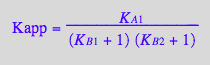
Summary of equations for equilibrium concentrations

Rtot= f(Leq, Leq and constants)

eq2_10

math

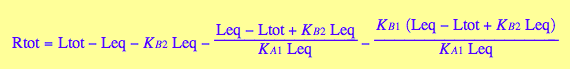
Analytical solution for [L]:

eq2_12

math

[R]

eq2_9

math

[L*]

eq2_6

[R*]

eq2_7

[RL]

eq2_8

Apparent binding constant (using full concentrations of unbound species)

eq2_19

math

Back to Contents

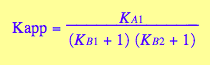
3. Define functions for equilibrium concentrations

Define functions for plotting and analysis

[L]

fLeq_U_R_L:= (Rtot, Ltot, K_A_1, K_B_1, K_B_2) --> eq2_12[2]

math

[R]

fReq_U_R_L:= (Rtot, Ltot, K_A_1, K_B_1, K_B_2) --> eq2_9[2] | eq2_12

math

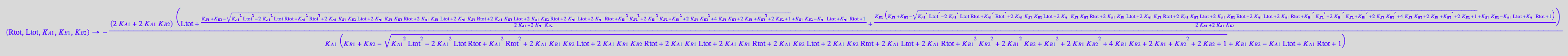
[R*]

fRstareq_U_R_L:= (Rtot, Ltot, K_A_1, K_B_1, K_B_2) --> eq2_7[2] | eq2_9 | eq2_12

math

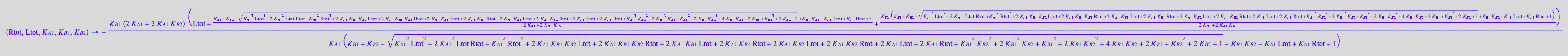
[L*]

fLstareq_U_R_L:= (Rtot, Ltot, K_A_1, K_B_1, K_B_2) --> eq2_6[2] | eq2_12

math

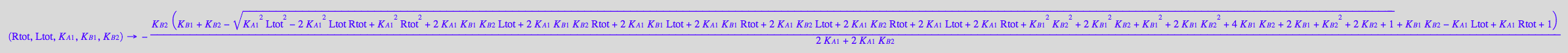
[RL]

fRLeq_U_R_L:= (Rtot, Ltot, K_A_1, K_B_1, K_B_2) --> eq2_8[2] | eq2_9 | eq2_12

math

Back to Contents

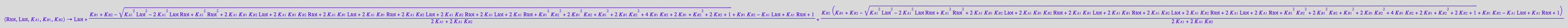
8. Save results on disk for future use

(you can retrieve them later by executing: fread(filename,Quiet))

ProjectName

Make "portable" equations (unique names for future use):

Rtot_U_R_L:=eq2_10;

Leq_U_R_L:=eq2_12;

Req_U_R_L:=eq2_9;

Lstareq_U_R_L:=eq2_6;

Rstareq_U_R_L:=eq2_7;

RLeq_U_R_L:=eq2_8;

Kapp_U_R_L:= eq2_19;

math

math

math

math

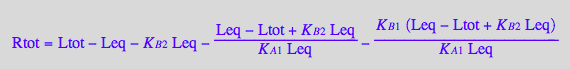
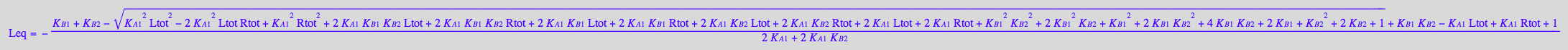
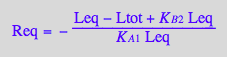
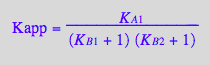
Save all numeric solutions:

filename:=CurrentPath.ProjectName.".mb";

write(filename,

// save basic equations

Rtot_U_R_L,

Leq_U_R_L,

Req_U_R_L,

Lstareq_U_R_L,

Rstareq_U_R_L,

RLeq_U_R_L,

Kapp_U_R_L,

// save functions

fLeq_U_R_L,

fReq_U_R_L,

fLstareq_U_R_L,

fRstareq_U_R_L,

fRLeq_U_R_L

)

Back to Contents

Conclusions

1. I derived analytical solutions for the U_R_L system

2. I also derived Rtot=f([L]) for numerical solution in Matlab

3. I will do test calculations in U_R_L_analysis.mn

Back to Contents