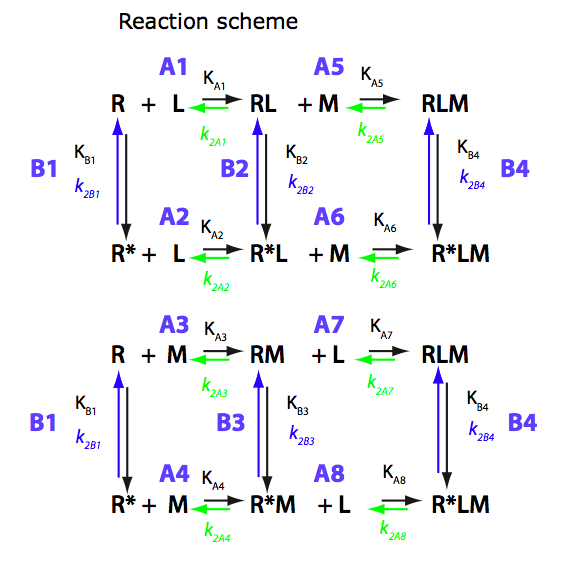
U-R-RL-RM_RLM_derivation

U-R-RL-RM-RLM

Binding of two ligands at non-mutually exclusive binding sites coupled with intramolecular isomerization of the receptor

(allosterically linked binding sites).

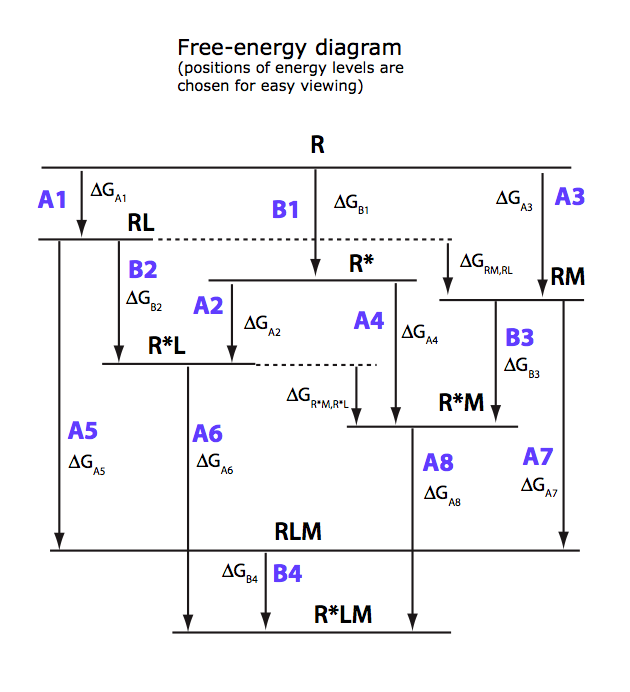
(images from

Equilibrium_models/U-R-RL-RM_RLM_model.pdf)

Contents

Goals

1. Definitions

2. Basic equilibrium equations

3. Derivation of equations for equilibrium concentrations

4. Prepare equations for a numeric solution

5. Save results on disk for future use

Conclusions

Back to Contents

Goals

In this notebook I will derive equations for two-ligand U-R-RL-RM-RLM model with separate (non-exclusive) binding sites and prepare equations for numerical simulations.

Analysis will be done in

EKM16.Analysis_of_multistep_kinetic_mechanisms/Equilibria/LRIM_U_R_RL_RM_RLM_analysis.mn

1. Definitions

clean up workspace

reset()

Set path to save results into:

ProjectName:="U_R_RL_RM_RLM";

CurrentPath:="/Users/kovrigin/Documents/Workspace/Data/Data.XV/EKM16.Analysis_of_multistep_kinetic_mechanisms/Equilibria/";

Binding and isomerization constants

All binding constants I am using are association constants.

These relationships serve as restraints for solve(), but not restrict these values in calculations!

K_A_1

K_A_1 ;

assumeAlso(K_A_1 > 0):

assumeAlso(K_A_1 , R_):

K_A_2

K_A_2 ;

assumeAlso(K_A_2 > 0):

assumeAlso(K_A_2 , R_):

K_A_3

K_A_3 ;

assumeAlso(K_A_3 > 0):

assumeAlso(K_A_3 , R_):

K_A_4

K_A_4 ;

assumeAlso(K_A_4 > 0):

assumeAlso(K_A_4 , R_):

K_A_5

K_A_5 ;

assumeAlso(K_A_5 > 0):

assumeAlso(K_A_5 , R_):

K_A_6

K_A_6 ;

assumeAlso(K_A_6 > 0):

assumeAlso(K_A_6 , R_):

K_A_7

K_A_7 ;

assumeAlso(K_A_7 > 0):

assumeAlso(K_A_7 , R_):

K_A_8

K_A_8 ;

assumeAlso(K_A_8 > 0):

assumeAlso(K_A_8 , R_):

Isomerization constants are formation constants for the alternative species

K_B_1

K_B_1 ;

assumeAlso(K_B_1 > 0):

assumeAlso(K_B_1 , R_):

K_B_2

K_B_2 ;

assumeAlso(K_B_2 > 0):

assumeAlso(K_B_2 , R_):

K_B_3

K_B_3 ;

assumeAlso(K_B_3 > 0):

assumeAlso(K_B_3 , R_):

K_B_4

K_B_4 ;

assumeAlso(K_B_4 > 0):

assumeAlso(K_B_4 , R_):

Total concentrations

Rtot - total concentration of the receptor

Rtot;

assumeAlso(Rtot>0):

assumeAlso(Rtot,R_):

Ltot - total concentration of the first ligand

Ltot;

assumeAlso(Ltot>0):

assumeAlso(Ltot,R_):

Mtot - total concentration of the second ligand

Mtot;

assumeAlso(Mtot>0):

assumeAlso(Mtot,R_):

Common equilibrium concentrations

Req - equilibrium concentration of a receptor monomer

Req;

assumeAlso(Req>0):

assumeAlso(Req<Rtot):

assumeAlso(Req,R_):

Rstareq - equilibrium concentration of an isomerized receptor monomer

Rstareq;

assumeAlso(Rstareq>0):

assumeAlso(Rstareq<Rtot):

assumeAlso(Rstareq,R_):

Leq - equilibrium concentration of a free ligand

Leq;

assumeAlso(Leq>0):

assumeAlso(Leq<Ltot):

assumeAlso(Leq,R_):

RLeq - equilibrium concentration of a receptor-ligand complex

RLeq;

assumeAlso(RLeq>0):

assumeAlso(RLeq<Rtot):

assumeAlso(RLeq,R_):

RstarLeq - equilibrium concentration of an isomerized receptor-ligand complex

RstarLeq;

assumeAlso(RstarLeq>0):

assumeAlso(RstarLeq<Rtot):

assumeAlso(RstarLeq,R_):

RMeq - equilibrium concentration of a receptor-ligand complex

RMeq;

assumeAlso(RMeq>0):

assumeAlso(RMeq<Rtot):

assumeAlso(RMeq,R_):

RstarMeq - equilibrium concentration of a receptor-ligand complex

RstarMeq;

assumeAlso(RstarMeq>0):

assumeAlso(RstarMeq<Rtot):

assumeAlso(RstarMeq,R_):

RLMeq - equilibrium concentration of a receptor-double-ligand complex

RLMeq;

assumeAlso(RLMeq>0):

assumeAlso(RLMeq<Rtot):

assumeAlso(RLMeq,R_):

RstarLMeq - equilibrium concentration of a receptor-ligand complex

RstarLMeq;

assumeAlso(RstarLMeq>0):

assumeAlso(RstarLMeq<Rtot):

assumeAlso(RstarLMeq,R_):

anames(Properties,User);

math

Back to Contents

2. Basic equilibrium equations

I will express Rtot as a function of Leq and all constants for numeric solution

Total concentrations of a receptor and a ligand

eq2_1:= Rtot = Req + Rstareq + RLeq + RstarLeq + RMeq + RstarMeq + RLMeq + RstarLMeq;

eq2_2:= Ltot = Leq + RLeq + RstarLeq + RLMeq + RstarLMeq;

eq2_3:= Mtot = Meq + RMeq + RstarMeq + RLMeq + RstarLMeq;

Write equilibrium thermodynamics equations (KA2 and KA4 are chosen to be dependent constants).

eq2_4:= K_A_1 = RLeq / (Req*Leq)

math

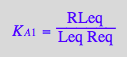
eq2_5:= K_A_2 = RstarLeq / (Rstareq*Leq) // !!! Dependent constant

math

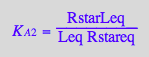
eq2_6:= K_A_3 = RMeq / (Req*Meq)

math

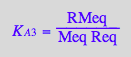
eq2_7:= K_A_4 = RstarMeq / (Rstareq*Meq) // !!! Dependent constant

math

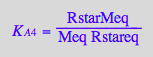
eq2_8:= K_A_5 = RLMeq / (RLeq*Meq)

math

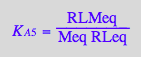
eq2_9:= K_A_6 = RstarLMeq / (RstarLeq*Meq) // !!! Dependent constant

math

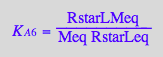
eq2_10:= K_A_7 = RLMeq /(RMeq*Leq)

math

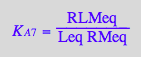
eq2_11:= K_A_8 = RstarLMeq/(RstarMeq*Leq) // !!! Dependent constant

math

eq2_12:= K_B_1 = Rstareq / Req

math

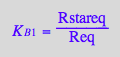
eq2_13:= K_B_2 = RstarLeq / RLeq

math

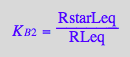
eq2_14:= K_B_3 = RstarMeq / RMeq

math

eq2_15:= K_B_4 = RstarLMeq / RLMeq

math

Back to Contents

3. Derivation of equations for equilibrium concentrations

Try to express Leq as a function of all constants and total concentrations

Express RstarLMeq

eq2_15;

solve(%,RstarLMeq);

%[1][1];

eq3_1:= RstarLMeq=%

math

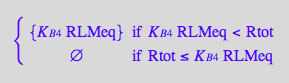
Express RstarMeq

eq2_14;

solve(%,RstarMeq);

%[1][1];

eq3_2:= RstarMeq=%

math

Express RstarLeq

eq2_13;

solve(eq2_13,RstarLeq);

%[1][1];

eq3_3:= RstarLeq = %

math

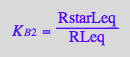
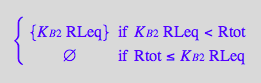
Express Rstareq

eq2_12;

solve(eq2_12,Rstareq);

%[1][1];

eq3_4:= Rstareq = %

math

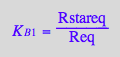
Express RLMeq

eq2_10;

solve(eq2_10,RLMeq);

%[1][1];

eq3_5:= RLMeq = %

math

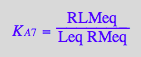
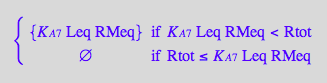
Express RMeq

eq2_6;

solve(eq2_6,RMeq);

%[1][1];

eq3_6:= RMeq = %

math

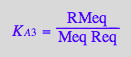
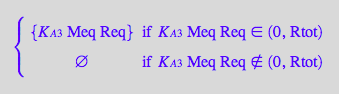
Express RLeq

eq2_4;

solve(eq2_4,RLeq);

%[1][1];

eq3_7:= RLeq = %

math

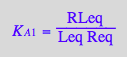
Substitute in mass conservation equations (begin with shorter ones for ligands)

eq2_2;

% | eq3_1;

% | eq3_3;

% | eq3_5;

% | eq3_6;

% | eq3_7;

eq3_8:= %:

Express [R] from there (keep [L] for last solving)

solve(eq3_8, Req);

%[1][1];

eq3_9:= Req = %

math

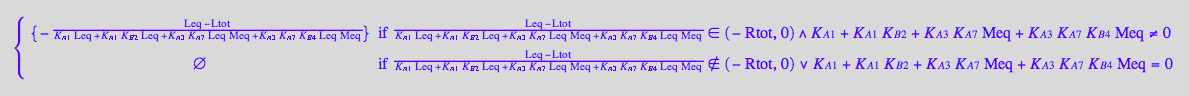
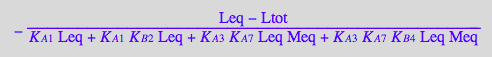
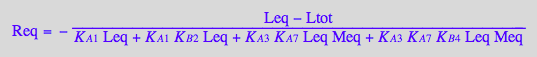
Use second ligand mass conservation law

eq2_3;

% | eq3_1;

% | eq3_2;

% | eq3_5;

% | eq3_6;

% | eq3_9;

eq3_10:= %:

math

Solve it for Meq

solutions3_10:=solve(eq3_10,Meq):

eq3_11:= solutions3_10[i,1] $ i=1..nops(solutions3_10):

nops(%)

How many independent soltions we have?

Is 1st solution a combination of 2nd and 3rd?

solution1:=eq3_11[4]: // a sequence of roots

solution2:=eq3_11[2][1]: // extract equation out of a sequence

solution3:=eq3_11[3][1]: // extract equation out of a sequence

if solution2 in solution1

then print(Unquoted,"First set of roots contains the second root.");

else print(Unquoted,"First set of roots DOES NOT contain the second root!");

end_if;

if solution3 in solution1

then print(Unquoted,"First set of roots contains the third root.");

else print(Unquoted,"First set of roots DOES NOT contain the third root!");

end_if;

First set of roots contains the second root.

First set of roots contains the third root.

Check correctness of the solutions by substitution into original equation solved:

Check first root

test1:= eq3_10 | Meq=solution2:

normal(%);

Check first root

test2:= eq3_10 | Meq=solution3:

normal(%);

Both solutions are correct.

Choose meaningful one for further work

solution2 | Leq=1 | Rtot=1 | Mtot=1 | Ltot=1 | K_A_1 =1 | K_A_3 =1 | K_A_5 =1 | K_A_7 =1 | K_A_8 =1 | K_B_1 =1 | K_B_2 =1 | K_B_3 =1 | K_B_4 =1 :

float(%)

solution3 | Leq=1 | Rtot=1 | Mtot=1 | Ltot=1 | K_A_1 =1 | K_A_3 =1 | K_A_5 =1 | K_A_7 =1 | K_A_8 =1 | K_B_1 =1 | K_B_2 =1 | K_B_3 =1 | K_B_4 =1 :

float(%)

Solution 3 is meaningful !

ASSIGN TO AN EQUATION:

eq3_12:= Meq = solution3:

NOTE: Here I did not pay attention, but A5 and A7 are dependent. Current equations are cast in A7. I will change it to A5 using relationship:

eq3_14:= K_A_7=K_A_1*K_A_5/K_A_3

math

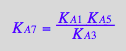
Finally, substitute all into a mass conservation law for a receptor (40 seconds to display!)

eq2_1;

% | eq3_1 ;

% | eq3_2 ;

% | eq3_3 ;

% | eq3_4 ;

% | eq3_5 ;

% | eq3_6 ;

% | eq3_7 ;

% | eq3_9 ;

% | eq3_12 :

% | eq3_14 :

eq3_13:=%:

math

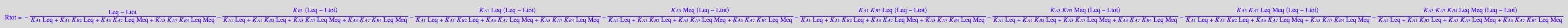
Summary of final equations

Reassign names for storage

ProjectName

Rtot=f([L])

Final equation (40 seconds to display!)

Rtot_U_R_RL_RM_RLM:=eq3_13:

[M]

Meq_U_R_RL_RM_RLM:=eq3_12 | eq3_14

math

[R]

Req_U_R_RL_RM_RLM:=eq3_9 | eq3_14

math

[RL]

RLeq_U_R_RL_RM_RLM:=eq3_7

[RM]

RMeq_U_R_RL_RM_RLM:=eq3_6

[RLM]

RLMeq_U_R_RL_RM_RLM:=eq3_5 | eq3_14

math

[R*]

Rstareq_U_R_RL_RM_RLM:=eq3_4

[R*L]

RstarLeq_U_R_RL_RM_RLM:=eq3_3

[R*M]

RstarMeq_U_R_RL_RM_RLM:=eq3_2

[R*LM]

RstarLMeq_U_R_RL_RM_RLM:=eq3_1

Test equations' consistency by expressing dependentt equilibrium constants:

eq2_5;

eq3_15:= KA2_U_R_RL_RM_RLM:= % | eq3_1 | eq3_2 | eq3_3 | eq3_4 | eq3_5 | eq3_6 | eq3_7 | eq3_9 | eq3_12 | eq3_13 ;

math

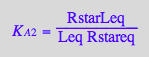
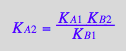
Correct !

eq2_7;

eq3_16:= KA4_U_R_RL_RM_RLM:= % | eq3_1 | eq3_2 | eq3_3 | eq3_4 | eq3_5 | eq3_6 | eq3_7 | eq3_9 | eq3_12 | eq3_13 ;

math

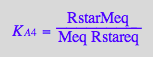
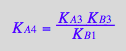
correct!

eq2_9;

eq3_17:= KA6_U_R_RL_RM_RLM:= % | eq3_1 | eq3_2 | eq3_3 | eq3_4 | eq3_5 | eq3_6 | eq3_7 | eq3_9 | eq3_12 | eq3_13 ;

math

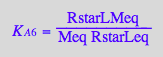
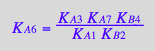
correct

eq2_11;

eq3_18:= KA8_U_R_RL_RM_RLM:= % | eq3_1 | eq3_2 | eq3_3 | eq3_4 | eq3_5 | eq3_6 | eq3_7 | eq3_9 | eq3_12 | eq3_13 ;

math

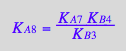
correct !

Back to Contents

5. Save results on disk for future use

(you can retrieve them later by executing: fread(filename,Quiet))

ProjectName

filename:=CurrentPath.ProjectName.".mb";

write(filename,

Rtot_U_R_RL_RM_RLM,

Meq_U_R_RL_RM_RLM,

Req_U_R_RL_RM_RLM,

RMeq_U_R_RL_RM_RLM,

RLeq_U_R_RL_RM_RLM,

Rstareq_U_R_RL_RM_RLM,

RstarMeq_U_R_RL_RM_RLM,

RstarLeq_U_R_RL_RM_RLM,

RLMeq_U_R_RL_RM_RLM,

RstarLMeq_U_R_RL_RM_RLM,

KA2_U_R_RL_RM_RLM,

KA4_U_R_RL_RM_RLM,

KA6_U_R_RL_RM_RLM,

KA8_U_R_RL_RM_RLM)