U_R_RL_derivation

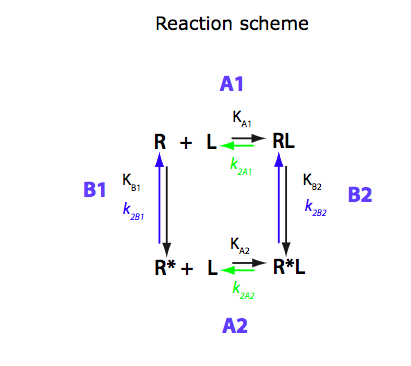
Derivation of equations for U-R-RL model

Binding of one ligand coupled with intramolecular isomerization

(this is the same model as ABC1, just in a new notation)

Contents

Goals

1. Definitions

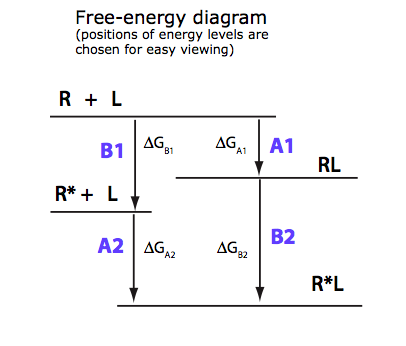
2. Derivation of a main equation

3. Define functions for equilibrium concentrations

4. Test if solution is meaningful

5. Check whether the solution satisfies all initial equation and conditions

6. Save results on disk for future use

Conclusions

Back to Contents

Goals

In this notebook I will re-derive equations for U-R-RL model (previously analyzed as ABC1) and prepare equations for numerical simulations.

Analysis will be done in

EKM16.Analysis_of_multistep_kinetic_mechanisms/Equilibria/LRIM_U_R_RL.analysis.mn

Back to Contents

1. Definitions

clean up workspace

reset()

Set path to save results into:

ProjectName:="U_R_RL";

CurrentPath:="/Users/kovrigin/Documents/Workspace/Data/Data.XV/EKM16.Analysis_of_multistep_kinetic_mechanisms/Equilibria/";

Binding and isomerization constants

All binding constants I am using are association constants.

These relationships serve as restraints for solve(), but not restrict these values in calculations!

K_A_1

K_A_1 ;

assumeAlso(K_A_1 > 0):

assumeAlso(K_A_1 , R_):

K_A_2

K_A_2 ;

assumeAlso(K_A_2 > 0):

assumeAlso(K_A_2 , R_):

Isomerization constants are formation constants for the alternative species

K_B_1

K_B_1 ;

assumeAlso(K_B_1 > 0):

assumeAlso(K_B_1 , R_):

K_B_2

K_B_2 ;

assumeAlso(K_B_2 > 0):

assumeAlso(K_B_2 , R_):

Total concentrations

Rtot - total concentration of the receptor

Rtot;

assumeAlso(Rtot>0):

assumeAlso(Rtot,R_):

Ltot - total concentration of a ligand

Ltot;

assumeAlso(Ltot>0):

assumeAlso(Ltot,R_):

Common equilibrium concentrations

Req - equilibrium concentration of a receptor monomer

Req;

assumeAlso(Req>0):

assumeAlso(Req<Rtot):

assumeAlso(Req,R_):

Rstareq - equilibrium concentration of an isomerized receptor monomer

Rstareq;

assumeAlso(Rstareq>0):

assumeAlso(Rstareq<Rtot):

assumeAlso(Rstareq,R_):

Leq - equilibrium concentration of a free ligand

Leq;

assumeAlso(Leq>0):

assumeAlso(Leq<Ltot):

assumeAlso(Leq,R_):

RLeq - equilibrium concentration of a receptor-ligand complex

RLeq;

assumeAlso(RLeq>0):

assumeAlso(RLeq<Rtot):

assumeAlso(RLeq,R_):

RstarLeq - equilibrium concentration of an isomerized receptor-ligand complex

RstarLeq;

assumeAlso(RstarLeq>0):

assumeAlso(RstarLeq<Rtot):

assumeAlso(RstarLeq,R_):

anames(Properties,User);

math

Back to Contents

2. Derivation of a main equation

Working equation: I will try to express analytical [L] from equation for a total concentration of a receptor or use the expression for a numeric solution if analytical is not possible

Total concentrations of a receptor and a ligand

eq2_1:= Rtot = Req + Rstareq + RLeq + RstarLeq;

eq2_2:= Ltot = Leq + RLeq + RstarLeq

Write equilibrium thermodynamics equations

eq2_3:= K_A_1 = RLeq / (Req*Leq)

math

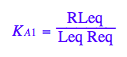
The following constant as chosen to be dependent in the model setup (don't use this equation in the solution):

eq2_4:= K_A_2 = RstarLeq / (Rstareq*Leq)

math

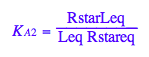
eq2_5:= K_B_1 = Rstareq/Req

math

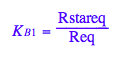
eq2_6:= K_B_2 = RstarLeq/RLeq

math

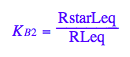
Try to express Leq as a function of all constants and total concentrations

Express RstarLeq

eq2_6;

solve(%,RstarLeq);

%[1][1];

eq2_7:= RstarLeq= %

math

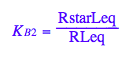
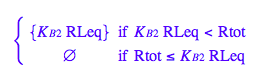
Express Rstareq

eq2_4;

% | eq2_7;

solve(%,Rstareq);

eq2_8:= Rstareq = %[1][1]

math

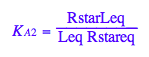
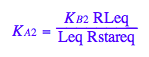
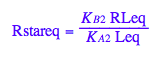
Express RLeq

eq2_5;

% | eq2_8;

solve(%,RLeq);

eq2_9:= RLeq = %[1][1]

math

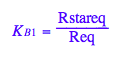
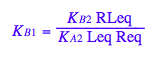
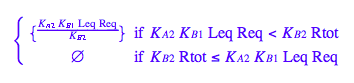
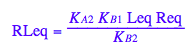
Check for mistakes in the equilbrium constants formulas:

Express Req using last equation left

eq2_3;

% | eq2_9;

math

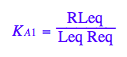
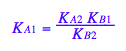
Nice!!! We arrived at the expected identity as one of the constants is dependent on the others!

Enter all equilibrium concentrations in equations for total concentrations:

eq2_1;eq2_2;

Substitute all receptor forms:

eq2_1;

% | eq2_7;

% | eq2_8;

% | eq2_9;

eq2_10:= %:

math

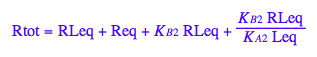
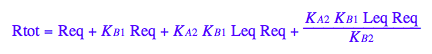
Express Req

solve(eq2_10,Req);

%[1];

eq2_11:= Req = %

math

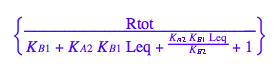
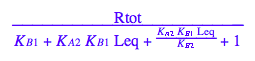
Substitute all ligand forms and Req

eq2_2;

% | eq2_7;

% | eq2_9;

% | eq2_11;

eq2_12:= %:

math

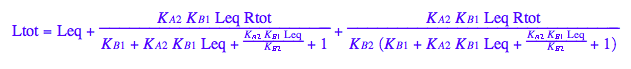
Solve for Leq

solutions2_12:=solve(eq2_12,Leq)

math

Extract solutions

eq2_13:= solutions2_12[i,1] $ i=1..nops(solutions2_12);

nops(%)

math

Is 1st solution a combination of 2nd and 3rd?

solution1:=eq2_13[1]; // a sequence of roots

solution2:=eq2_13[2][1]; // extract equation out of a sequence

solution3:=eq2_13[3][1]; // extract equation out of a sequence

if solution2 in solution1

then print(Unquoted,"First set of roots contains the second root.");

else print(Unquoted,"First set of roots DOES NOT contain the second root!");

end_if;

if solution3 in solution1

then print(Unquoted,"First set of roots contains the third root.");

else print(Unquoted,"First set of roots DOES NOT contain the third root!");

end_if;

math

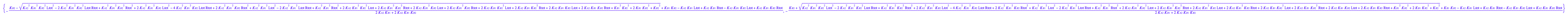
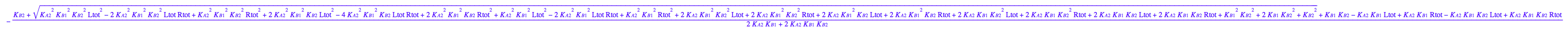
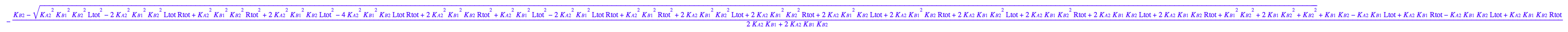
First set of roots contains the second root.

First set of roots contains the third root.

Check correctness of the solutions by substitution into original equation solved:

Check first root

test1:= eq2_12 | Leq=solution2;

normal(%);

math

Check second root

test2:= eq2_12 | Leq=solution3;

normal(%);

math

Both solutions are correct.

Back to Contents

3. Define functions for equilibrium concentrations

Define functions for plotting and analysis

Choose one solution (tested for being meaningful later)

eq3_1:= Leq = solution3;

math

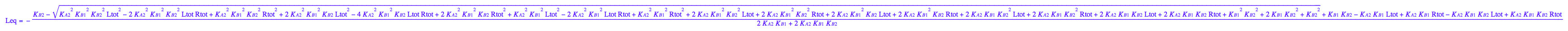
Express dependent constant:

eq2_3;

% | eq2_9;

solve(%,K_A_2);

%[1];

eq3_2:= K_A_2= %

math

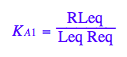
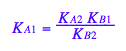
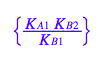
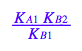
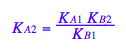
Remove dependent constant from all equations

eq3_1;

eq3_4:= eq3_1 | eq3_2;

math

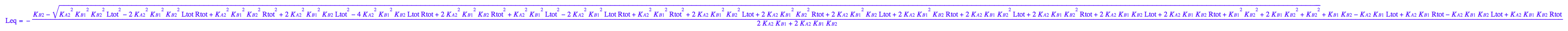
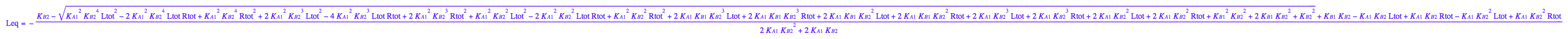
eq2_11;

eq3_5:= eq2_11 | eq3_4 | eq3_2;

math

eq2_9;

eq3_6:= % | eq3_4 | eq3_5 | eq3_2

math

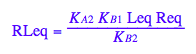
eq2_8;

eq3_7:= % | eq3_6 | eq3_4 | eq3_2;

math

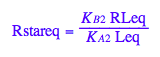
eq2_7;

eq3_8:= % | eq3_6;

math

Summary of equations for all species

Independent parameters:

Rtot, Ltot, K_A_1, K_B_1, K_B_2

Dependent constant

eq3_2

math

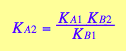
[L]

eq3_4

math

[R]

eq2_11

math

[RL]

eq2_9

math

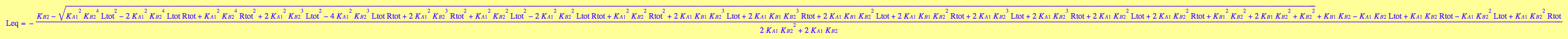
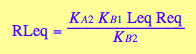
[R*]

eq2_8 | eq2_9

[R*L]

eq2_7 | eq2_9

Generate functions

fLeq:= (Rtot, Ltot, K_A_1, K_B_1, K_B_2) --> eq3_4[2]

math

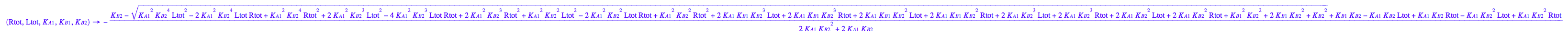
fReq:= (Rtot, Ltot, K_A_1, K_B_1, K_B_2) --> eq3_5[2]

math

fRLeq:= (Rtot, Ltot, K_A_1, K_B_1, K_B_2) --> eq3_6[2]

math

fRstareq:= (Rtot, Ltot, K_A_1, K_B_1, K_B_2) --> eq3_7[2]

math

fRstarLeq:= (Rtot, Ltot, K_A_1, K_B_1, K_B_2) --> eq3_8[2]

math

Back to Contents

4. Test if solution is meaningful

Set some realistic values for constants:

Total_R:=1e-3;

Total_L:=0.5e-3;

Ka1:=1e7;

Kb1:=1/1;

Kb2:=0.1;

Test that all equilibrium concentrations are positive values:

if (fLeq(Total_R, Total_L, Ka1, Kb1, Kb2)>0 and

fReq(Total_R, Total_L, Ka1, Kb1, Kb2)>0 and

fRLeq(Total_R, Total_L, Ka1, Kb1, Kb2)>0 and

fRstareq(Total_R, Total_L, Ka1, Kb1, Kb2)>0 and

fRstarLeq(Total_R, Total_L, Ka1, Kb1, Kb2)>0

)

then

print(Unquoted,"Solution is meaningful.");

else

print(Unquoted,"WARNING!!!!");

print(Unquoted,"Solution is NOT meaningful: some concentrations become negative!");

end_if

Solution is meaningful.

Back to Contents

5. Check whether the solution satisfies all initial equation and conditions

Here are all original independent

equations:

eq2_1;eq2_2;eq2_3;eq2_4;eq2_5;eq2_6;

math

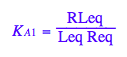
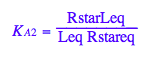
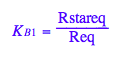
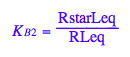
Test eq2_1

eq2_1;

% | eq3_4 | eq3_5 | eq3_6 | eq3_7 | eq3_8;

normal(%)

math

Test eq2_2

eq2_2;

% | eq3_4 | eq3_5 | eq3_6 | eq3_7 | eq3_8;

normal(%)

math

Test eq2_3

eq2_3;

% | eq3_4 | eq3_5 | eq3_6 | eq3_7 | eq3_8;

normal(%)

math

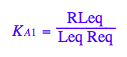
Test eq2_4

eq2_4;

% | eq3_4 | eq3_5 | eq3_6 | eq3_7 | eq3_8 | eq3_2;

normal(%)

math

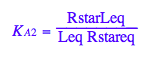
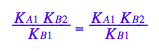
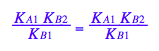
Test eq2_5

eq2_5;

% | eq3_4 | eq3_5 | eq3_6 | eq3_7 | eq3_8;

normal(%)

math

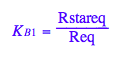
Test eq2_6

eq2_6;

% | eq3_4 | eq3_5 | eq3_6 | eq3_7 | eq3_8;

normal(%)

math

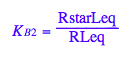
The found solution satisfies all original equations

Back to Contents

5. Save results on disk for future use

(you can retrieve them later by executing: fread(filename,Quiet))

ProjectName

eq2_7;eq2_8;eq2_9;eq2_10;eq2_11;

math

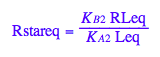
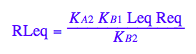
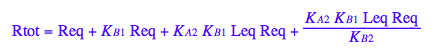
Generate Rtot=f([L]) equation for testing numerical routines against analytical solutions

eq2_2;

% | eq2_7;

% | eq2_9;

solve(%,Req);

%[1][1];

eq5_1:= Req = %;

math

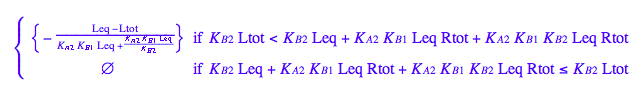
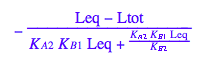
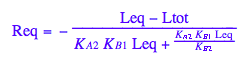
eq2_1;

% | eq2_7 | eq2_8 | eq2_9 | eq5_1 ;

% | eq3_2; // get rid of dependent KA2

eq5_2:= %:

math

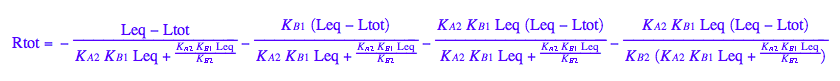
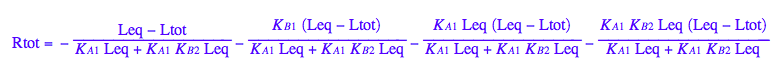
Here are solutions we want to save.

Reassign names

Rtot_U_R_RL:=eq5_2;

Leq_U_R_RL:=eq3_4:;

Req_U_R_RL:=eq3_5:;

RLeq_U_R_RL:=eq3_6:;

Rstareq_U_R_RL:=eq3_7:;

RstarLeq_U_R_RL:=eq3_8:;

KA2_U_R_RL:=eq3_2:;

math

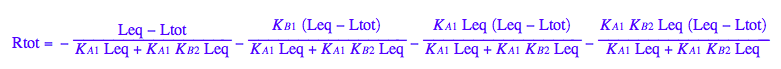
Reassign function names

fLeq_U_R_RL:=fLeq:

fReq_U_R_RL:=fReq:

fRLeq_U_R_RL:=fRLeq:

fRstareq_U_R_RL:=fRstareq:

fRstarLeq_U_R_RL:=fRstarLeq:

ProjectName

filename:=CurrentPath.ProjectName.".mb";

write(filename,Rtot_U_R_RL,Leq_U_R_RL, Req_U_R_RL, RLeq_U_R_RL, Rstareq_U_R_RL, RstarLeq_U_R_RL, KA2_U_R_RL,

fLeq_U_R_RL,fReq_U_R_RL,fRLeq_U_R_RL,fRstareq_U_R_RL,fRstarLeq_U_R_RL)

Conclusions

1. I derived analytical solutions for the U_R_RL system

2. I also derived and saved Rtot=f([L]) for numerical solution

Back to Contents