![]()

U model (analysis)
Binding of one ligand molecules to one receptor monomer
R + L = RL
Evgenii L. Kovrigin
01-15-2014
Here I am analyzing the U model solution
clean up workspace
reset()
STEP 1: Set path to saved derivation results
NOTE: make sure the path ends with slash character "/".
ProjectName:="U_model_derivation";
CurrentPath:="/Volumes/Leopard_Partition/Users/kovrigin/Documents/Workspace/Global Analysis/IDAP/Mathematical_models/Equilibrium_thermodynamic_models/U/";
![]()

Read results of derivations
filename:=CurrentPath.ProjectName.".mb";
fread(filename,Quiet):
anames(User);

![]()
STEP 2: Assume values and test procedures:
Rtot_value:=1e-3:
K_A_value:= 1e7:
LR_ratio_value:= 0.8:
Test calculations:
fLeq_U(Rtot_value, LR_ratio_value, K_A_value);
pnReq_U(Rtot_value, LR_ratio_value, K_A_value);
pnRLeq_U(Rtot_value, LR_ratio_value, K_A_value);
![]()
![]()
![]()
=> all operational
STEP 3: Make wrapper functions for plotting dependent only on one parameter x=L/R:
fnLeq_U:=x -> fLeq_U(Rtot_value, x, K_A_value):
fnReq_U:=x -> pnReq_U(Rtot_value, x, K_A_value):
fnRLeq_U:=x -> pnRLeq_U(Rtot_value, x, K_A_value):
2.1 Macroscopic B model
ModelName:="U":
// Thermodynamic parameters
Rtot_value:=1e-3:
K_A_value:= 1e5:
LR_ratio_max:= 1.5:
// Plotting parameters
LW:=1: x_min:=1e-6:
// Compute dependent constants
// None in this model
p_Leq:= plot::Function2d(Function=(fnLeq_U), LegendText="[L]", Color = RGB::Green, XMin=(x_min),XMax=(LR_ratio_max),XName=(x),TitlePositionX=(0) ,LineWidth=LW):
p_Req:= plot::Function2d(Function=(fnReq_U), LegendText="[R]", Color = RGB::Black, XMin=(x_min),XMax=(LR_ratio_max),XName=(x),TitlePositionX=(0) ,LineWidth=LW):
p_RLeq:= plot::Function2d(Function=(fnRLeq_U), LegendText="[RL]", Color = RGB::Blue, XMin=(x_min),XMax=(LR_ratio_max),XName=(x),TitlePositionX=(0) ,LineWidth=LW):
// Report constants
print(Unquoted,"Model: ".ModelName);
print(Unquoted,"R(total):=".Rtot_value.":");
print(Unquoted,"K_A:=".K_A_value.":");
// Plot all
// plot all together
plot(p_Leq,p_Req, p_RLeq, YAxisTitle="M", Header=("Model: ".ProjectName), Height=160, Width=100,TicksLabelFont=["Helvetica",12,[0,0,0],Left], AxesTitleFont=["Helvetica",14,[0,0,0],Left], XGridVisible=TRUE, YGridVisible=TRUE,LegendVisible=TRUE, LegendFont=["Helvetica",14,[0,0,0],Left]);
Model: U
R(total):=0.001:
K_A:=100000.0: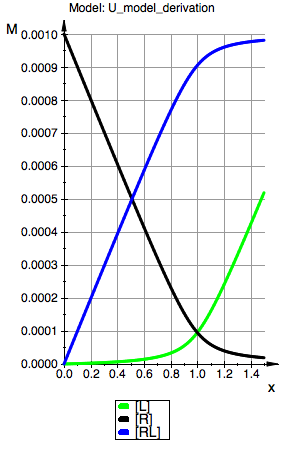
Conclusions
U model is ready for use in IDAP.