![]()

U models (derivation)
Binding of one ligand molecules to one receptor monomer
R + L = RL
Evgenii L. Kovrigin
01-15-2014
2. Basic equilibrium equations
3. Analysis of statistical effects on binding and kinetic constants
4. Derivation of equations for concentrations of species
5. Prepare equations for a numeric solution
6. Save results on disk for future use
1. define thermodynamic equations for binding of one ligand to one receptor molecule .
2. prepare equations for calculations of equilibrium concentrations in the titration experiment.
Analysis of the solutions will be done separately.
clean up workspace
reset()
Set path to save results into:
NOTE: make sure the path ends with slash character "/".
ProjectName:="U_model_derivation";
CurrentPath:="/Volumes/Leopard_Partition/Users/kovrigin/Documents/Workspace/Global Analysis/IDAP/Mathematical_models/Equilibrium_thermodynamic_models/U/";
![]()

Binding constant
NOTE 1: All binding constants I am using are association constants.
NOTE 2: These relationships serve as restraints for solve(), but not restrict these values in calculations!
Macroscopic equilibrium constants
K_A
K_A ;
assumeAlso(K_A > 0):
assumeAlso(K_A , R_):
![]()
Total concentrations
Rtot - total concentration of the receptor
Rtot;
assumeAlso(Rtot>0):
assumeAlso(Rtot,R_):
![]()
Ltot - total concentration of a ligand
Ltot;
assumeAlso(Ltot>0):
assumeAlso(Ltot,R_):
![]()
Equilibrium concentrations
Req - free receptor
Req;
assumeAlso(Req>0):
assumeAlso(Req<Rtot):
assumeAlso(Req,R_):
![]()
Leq - free ligand
Leq;
assumeAlso(Leq>0):
assumeAlso(Leq<Ltot):
assumeAlso(Leq,R_):
![]()
RLeq - equlibrium conentration of single-bound species
RLeq;
assumeAlso(RLeq>0):
assumeAlso(RLeq<Rtot):
assumeAlso(RLeq<Ltot):
assumeAlso(RLeq,R_):
![]()
Check if all names are correctly entered:
anames(Properties,User);
![]()
2. Basic equilibrium equations
Goal: I will try to express analytical [L] from equation for a total concentration of a receptor or use the expression for a numeric solution if analytical is not possible
Total concentration (mass balance) equations:
eq2_1:= Rtot = Req + RLeq;
eq2_2:= Ltot = Leq + RLeq ;
![]()
![]()
Equilibrium thermodynamics equations for independent constants
eq2_3:= K_A = RLeq / (Req*Leq);
![]()
4. Derivation of equations for concentrations of species
Goal: Express concentration of the free ligand, Leq, as a function of equilibrium constants and total concentrations.
Equations to use:
eq2_1
![]()
eq2_2
![]()
eq2_3
![]()
STEP 1: Express all R-containing species starting from the higher stoichiometry
Express RL_2eq out of the equilibrium constant equation
eq2_3:
solve(%, RLeq):
%[1][1]:
eq4_1:= RLeq = %
![]()
STEP 2: Substitute all into mass balance for L and express Req
eq2_2:
% | eq4_1:
eq4_2:= %
![]()
solve(eq4_2,Req):
%[1][1]:
eq4_3:= Req = %
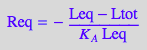
STEP 3: Substitute all into mass balance for R and attempt to solve for Leq
eq2_1:
% | eq4_1 | eq4_3:
eq4_4:= %;
normal(%);
eq4_5:=Simplify(%);
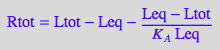
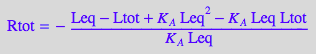
![]()
=> This is an expression for numerical solution
Try to solve analytically
solutions:=solve(eq4_5, Leq);
![piecewise([(K_A^2*Ltot^2 - 2*K_A^2*Ltot*Rtot + K_A^2*Rtot^2 + 2*K_A*Ltot + 2*K_A*Rtot + 1)^(1/2) + K_A*Rtot + 1 < K_A*Ltot and 2*K_A^2*Ltot*Rtot <= K_A^2*Ltot^2 + K_A^2*Rtot^2 + 2*K_A*Ltot + 2*K_A*Rtot + 1 and ((K_A^2*Ltot^2 - 2*K_A^2*Ltot*Rtot + K_A^2*Rtot^2 + 2*K_A*Ltot + 2*K_A*Rtot + 1)^(1/2) + K_A*Ltot - K_A*Rtot - 1)/(2*K_A) < Ltot and -((K_A^2*Ltot^2 - 2*K_A^2*Ltot*Rtot + K_A^2*Rtot^2 + 2*K_A*Ltot + 2*K_A*Rtot + 1)^(1/2) - K_A*Ltot + K_A*Rtot + 1)/(2*K_A) < Ltot and K_A*Rtot + 1 < (K_A^2*Ltot^2 - 2*K_A^2*Ltot*Rtot + K_A^2*Rtot^2 + 2*K_A*Ltot + 2*K_A*Rtot + 1)^(1/2) + K_A*Ltot, {-((K_A^2*Ltot^2 - 2*K_A^2*Ltot*Rtot + K_A^2*Rtot^2 + 2*K_A*Ltot + 2*K_A*Rtot + 1)^(1/2) - K_A*Ltot + K_A*Rtot + 1)/(2*K_A), ((K_A^2*Ltot^2 - 2*K_A^2*Ltot*Rtot + K_A^2*Rtot^2 + 2*K_A*Ltot + 2*K_A*Rtot + 1)^(1/2) + K_A*Ltot - K_A*Rtot - 1)/(2*K_A)}], [(not (K_A^2*Ltot^2 - 2*K_A^2*Ltot*Rtot + K_A^2*Rtot^2 + 2*K_A*Ltot + 2*K_A*Rtot + 1)^(1/2) + K_A*Rtot + 1 < K_A*Ltot or not -((K_A^2*Ltot^2 - 2*K_A^2*Ltot*Rtot + K_A^2*Rtot^2 + 2*K_A*Ltot + 2*K_A*Rtot + 1)^(1/2) - K_A*Ltot + K_A*Rtot + 1)/(2*K_A) < Ltot) and 2*K_A^2*Ltot*Rtot <= K_A^2*Ltot^2 + K_A^2*Rtot^2 + 2*K_A*Ltot + 2*K_A*Rtot + 1 and ((K_A^2*Ltot^2 - 2*K_A^2*Ltot*Rtot + K_A^2*Rtot^2 + 2*K_A*Ltot + 2*K_A*Rtot + 1)^(1/2) + K_A*Ltot - K_A*Rtot - 1)/(2*K_A) < Ltot and K_A*Rtot + 1 < (K_A^2*Ltot^2 - 2*K_A^2*Ltot*Rtot + K_A^2*Rtot^2 + 2*K_A*Ltot + 2*K_A*Rtot + 1)^(1/2) + K_A*Ltot, {((K_A^2*Ltot^2 - 2*K_A^2*Ltot*Rtot + K_A^2*Rtot^2 + 2*K_A*Ltot + 2*K_A*Rtot + 1)^(1/2) + K_A*Ltot - K_A*Rtot - 1)/(2*K_A)}], [(K_A^2*Ltot^2 - 2*K_A^2*Ltot*Rtot + K_A^2*Rtot^2 + 2*K_A*Ltot + 2*K_A*Rtot + 1)^(1/2) + K_A*Rtot + 1 < K_A*Ltot and 2*K_A^2*Ltot*Rtot <= K_A^2*Ltot^2 + K_A^2*Rtot^2 + 2*K_A*Ltot + 2*K_A*Rtot + 1 and (not ((K_A^2*Ltot^2 - 2*K_A^2*Ltot*Rtot + K_A^2*Rtot^2 + 2*K_A*Ltot + 2*K_A*Rtot + 1)^(1/2) + K_A*Ltot - K_A*Rtot - 1)/(2*K_A) < Ltot or not K_A*Rtot + 1 < (K_A^2*Ltot^2 - 2*K_A^2*Ltot*Rtot + K_A^2*Rtot^2 + 2*K_A*Ltot + 2*K_A*Rtot + 1)^(1/2) + K_A*Ltot) and -((K_A^2*Ltot^2 - 2*K_A^2*Ltot*Rtot + K_A^2*Rtot^2 + 2*K_A*Ltot + 2*K_A*Rtot + 1)^(1/2) - K_A*Ltot + K_A*Rtot + 1)/(2*K_A) < Ltot, {-((K_A^2*Ltot^2 - 2*K_A^2*Ltot*Rtot + K_A^2*Rtot^2 + 2*K_A*Ltot + 2*K_A*Rtot + 1)^(1/2) - K_A*Ltot + K_A*Rtot + 1)/(2*K_A)}], [(((K_A^2*Ltot^2 - 2*K_A^2*Ltot*Rtot + K_A^2*Rtot^2 + 2*K_A*Ltot + 2*K_A*Rtot + 1)^(1/2) + K_A*Ltot - K_A*Rtot - 1)/(2*K_A) < Ltot and K_A*Rtot + 1 < (K_A^2*Ltot^2 - 2*K_A^2*Ltot*Rtot + K_A^2*Rtot^2 + 2*K_A*Ltot + 2*K_A*Rtot + 1)^(1/2) + K_A*Ltot or (K_A^2*Ltot^2 - 2*K_A^2*Ltot*Rtot + K_A^2*Rtot^2 + 2*K_A*Ltot + 2*K_A*Rtot + 1)^(1/2) + K_A*Rtot + 1 < K_A*Ltot and (not ((K_A^2*Ltot^2 - 2*K_A^2*Ltot*Rtot + K_A^2*Rtot^2 + 2*K_A*Ltot + 2*K_A*Rtot + 1)^(1/2) + K_A*Ltot - K_A*Rtot - 1)/(2*K_A) < Ltot or not K_A*Rtot + 1 < (K_A^2*Ltot^2 - 2*K_A^2*Ltot*Rtot + K_A^2*Rtot^2 + 2*K_A*Ltot + 2*K_A*Rtot + 1)^(1/2) + K_A*Ltot) and -((K_A^2*Ltot^2 - 2*K_A^2*Ltot*Rtot + K_A^2*Rtot^2 + 2*K_A*Ltot + 2*K_A*Rtot + 1)^(1/2) - K_A*Ltot + K_A*Rtot + 1)/(2*K_A) < Ltot) and K_A^2*Ltot^2 + K_A^2*Rtot^2 + 2*K_A*Ltot + 2*K_A*Rtot + 1 < 2*K_A^2*Ltot*Rtot or not (K_A^2*Ltot^2 - 2*K_A^2*Ltot*Rtot + K_A^2*Rtot^2 + 2*K_A*Ltot + 2*K_A*Rtot + 1)^(1/2) + K_A*Rtot + 1 < K_A*Ltot and not K_A*Rtot + 1 < (K_A^2*Ltot^2 - 2*K_A^2*Ltot*Rtot + K_A^2*Rtot^2 + 2*K_A*Ltot + 2*K_A*Rtot + 1)^(1/2) + K_A*Ltot or (K_A^2*Ltot^2 - 2*K_A^2*Ltot*Rtot + K_A^2*Rtot^2 + 2*K_A*Ltot + 2*K_A*Rtot + 1)^(1/2) + K_A*Rtot + 1 < K_A*Ltot and not -((K_A^2*Ltot^2 - 2*K_A^2*Ltot*Rtot + K_A^2*Rtot^2 + 2*K_A*Ltot + 2*K_A*Rtot + 1)^(1/2) - K_A*Ltot + K_A*Rtot + 1)/(2*K_A) < Ltot and not K_A*Rtot + 1 < (K_A^2*Ltot^2 - 2*K_A^2*Ltot*Rtot + K_A^2*Rtot^2 + 2*K_A*Ltot + 2*K_A*Rtot + 1)^(1/2) + K_A*Ltot or (not (K_A^2*Ltot^2 - 2*K_A^2*Ltot*Rtot + K_A^2*Rtot^2 + 2*K_A*Ltot + 2*K_A*Rtot + 1)^(1/2) + K_A*Rtot + 1 < K_A*Ltot or not -((K_A^2*Ltot^2 - 2*K_A^2*Ltot*Rtot + K_A^2*Rtot^2 + 2*K_A*Ltot + 2*K_A*Rtot + 1)^(1/2) - K_A*Ltot + K_A*Rtot + 1)/(2*K_A) < Ltot) and not ((K_A^2*Ltot^2 - 2*K_A^2*Ltot*Rtot + K_A^2*Rtot^2 + 2*K_A*Ltot + 2*K_A*Rtot + 1)^(1/2) + K_A*Ltot - K_A*Rtot - 1)/(2*K_A) < Ltot and K_A*Rtot + 1 < (K_A^2*Ltot^2 - 2*K_A^2*Ltot*Rtot + K_A^2*Rtot^2 + 2*K_A*Ltot + 2*K_A*Rtot + 1)^(1/2) + K_A*Ltot, {}])](U_model_derivation_images/math21.png)
=> multipe solutions. Select the positive one:
sol1:=solutions[2][1];
sol2:=solutions[3][1];
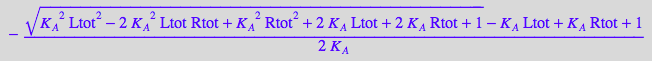
Test
sol1 | Ltot=1 | Rtot = 1 | K_A=1;
bool(%>0)
![]()
![]()
sol2 | Ltot=1 | Rtot = 1 | K_A=1;
bool(%>0)
![]()
![]()
Use positivie solution!
eq4_6:= Leq = sol1
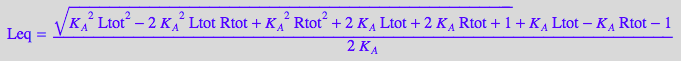
Summary of equations for equilibrium concentrations of species
NOTE: Rename all equations for easier use.
Expression for analytical solution for Leq:
eqLeq:=eq4_6
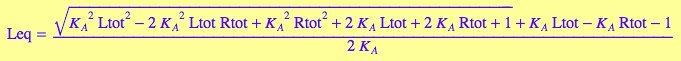
Expressions for other species
eqReq:=eq4_3
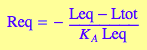
eqRLeq:=eq4_1
![]()
Introduce a convenient variable LRratio=Ltot/Rtot
eqLRratio:= Ltot = LRratio * Rtot
![]()
5.1 Macroscopic B model
STEP 1: Make a function forLeq
fLeq_U:= (Rtot, LRratio, K_A) --> eqLeq[2] | eqLRratio;
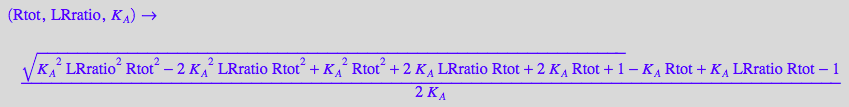
Assume some constant values for testing
NOTE 1: Use different names for variables!!!
NOTE 2: Make sure the VALUES are all different and NOT just ORDER OF MAGNITUDS to make it easier for troubleshooting.
Rtot_value:=1e-3:
K_A_value:= 1e4:
LR_ratio_max:= 2.5:
LR_ratio_value:= 0.8:
Test operation of the new function:
fLeq_U(Rtot_value, LR_ratio_value, K_A_value)
![]()
=> operational!
STEP 3: Define functions for equilibrium concentrations of all species
(begin with listing equations for the species)
Expressions for other species:
eqReq:
pnReq_U:= proc(paramRtot, paramLRratio, paramK_A)
local L;
begin
L:=fLeq_U(paramRtot, paramLRratio, paramK_A);
// Insert equation for this species and substitute all parameters
eqReq[2] | Ltot=paramLRratio*paramRtot | Leq=L | K_A=paramK_A
end_proc
![]()
test
pnReq_U(Rtot_value, LR_ratio_value, K_A_value);
![]()
=>operational
RLeq
eqRLeq;
pnRLeq_U:= proc(paramRtot, paramLRratio, paramK_A)
local L, R;
begin
L:=fLeq_U(paramRtot, paramLRratio, paramK_A);
R:=pnReq_U(paramRtot, paramLRratio, paramK_A);
// Insert equation for this species and substitute all parameters
eqRLeq[2] | Leq=L | Req=R | K_A=paramK_A ;
end_proc
![]()
![]()
Test
pnRLeq_U(Rtot_value, LR_ratio_value, K_A_value);
![]()
=> operational
STEP 4: Catch errors in substitution of equations (cut-and-paste glitches)
Collect all the test lines and re-run. Make sure all numbers come out different.
Cut-and-paste glitches come out as identical numbers.
fLeq_U(Rtot_value, LR_ratio_value, K_A_value);
pnReq_U(Rtot_value, LR_ratio_value, K_A_value);
pnRLeq_U(Rtot_value, LR_ratio_value, K_A_value);
![]()
![]()
![]()
=> All different! No cut-and-paste typos.
STEP 5: Collect all these names in Section 6 for saving on the disk.
6. Save results on disk for future use
(you can retrieve them later by executing: fread(filename,Quiet))
ProjectName;
CurrentPath
![]()

Save all numeric solutions:
filename:=CurrentPath.ProjectName.".mb";
write(filename,
// - equations
eqLeq,
eqReq,
eqRLeq,
// - procedures
fLeq_U,
pnReq_U,
pnRLeq_U
)

Conclusions
Derivation has been completed. Analysis document confirms correctness of the model