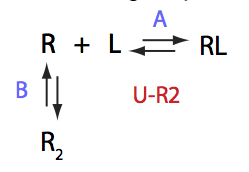
U-R2

Derivation of differential equations describing evolution of spin populations

image

 

 

 

 

Contents

 

 

1. Reaction rates and partial conversion rates

 

3. Net conversion rates

 

4. Expression in terms of spin (monomer) concentrations

 

5. Final result

 

Conclusions

 

 

 

 

Back to Contents

 

 

 

 

 

 

1. Reaction rates and partial conversion rates

clean up workspace

reset()

 

 

 

Write properly balanced reactions equations:

 

Transition A:

(1)          (2)

R+L<=>RL

Constants: k_1_A, k_2_A.

 

 

 

Transition B:

(1)          (2)

2R <=> R2

Constants: k_1_B, k_2_B.

 

 

 

 

Write reaction rates

We distinguish reaction rates ( Rate, elementary reaction acts per unit time) and conversion rates (dc/dt, number of moles of specific species consumed/produced per unit time). Conversion rates, dc/dt, for species are related to reaction rates, Rate, through molecularity coefficients.

 

We also distinguish here partial conversion rates from net (overall) conversion rates. The net conversion rate is actual rate of change in measured concentration of the species. Partial conversion rate is the conversion rate of the species along a specific branch of the reaction mechanism. Summing partial conversion rates of the species one obtains the net conversion rate.

 

 

Ligand binding rates (forward transition on A: 1_A)

 

a reaction rate

eq1_1a:=Rate_1_A = k_1_A*R*L

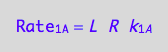
Rate_1_A = L*R*k_1_A

a partial conversion rate of R

eq1_1b:= dcRdt_1_A = Rate_1_A

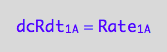
dcRdt_1_A = Rate_1_A

The final form

eq1_1c:= eq1_1b | eq1_1a

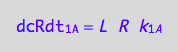
dcRdt_1_A = L*R*k_1_A

 

 

 

Ligand dissociation rates (reverse transition on A: 2_A)

 

a reaction rate

eq1_2a:=Rate_2_A = k_2_A*RL

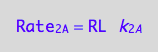
Rate_2_A = RL*k_2_A

a partial conversion rate of RL

eq1_2b:= dcRLdt_2_A = Rate_2_A

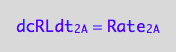
dcRLdt_2_A = Rate_2_A

The final form

eq1_2c:= eq1_2b | eq1_2a

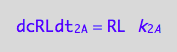
dcRLdt_2_A = RL*k_2_A

 

 

 

Receptor dimerization rates (forward transition on B: 1_B)

 

a reaction rate

eq1_3a:= Rate_1_B = k_1_B*R*R

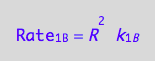
Rate_1_B = R^2*k_1_B

a partial conversion rate of R

(two molecules are involved in one reaction act)

eq1_3b:= dcRdt_1_B = 2* Rate_1_B

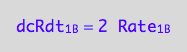
dcRdt_1_B = 2*Rate_1_B

The final form

eq1_3c:= eq1_3b | eq1_3a

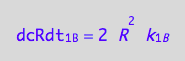
dcRdt_1_B = 2*R^2*k_1_B

 

 

 

Receptor dissociation rates (reverse transition on B: 1_B)

 

a reaction rate

eq1_4a:= Rate_2_B = k_2_B * R2

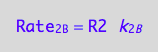
Rate_2_B = R2*k_2_B

a partial conversion rate of R2

eq1_4b:= dcR2dt_2_B = Rate_2_B

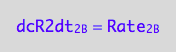
dcR2dt_2_B = Rate_2_B

The final form

eq1_4c:= eq1_4b |eq1_4a

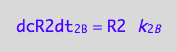
dcR2dt_2_B = R2*k_2_B

 

 

 

Back to Contents

 

 

 

 

 

 

 

3. Net conversion rates

 

To define evolution of the species we need to compute concentrations  as a function of time. To this end, we will write differential equations for conversion rates of all species.

 

In a reversible process both forward and reverse reaction occur simultaneously. Thus, the net conversion rate of the species is a difference between partial conversion rates resulting from forward and reverse reactions, summed along all branches.

 

Net conversion rate of  R

 

Sum all pertaining partial rates with respective signs

eq3_1:= dcRdt_N = -dcRdt_1_A + dcRdt_2_A -dcRdt_1_B + dcRdt_2_B

dcRdt_N = dcRdt_2_A - dcRdt_1_B - dcRdt_1_A + dcRdt_2_B

Let's determine what the terms are.

 

The forward terms were defined above:

eq1_1c;
eq1_3c;

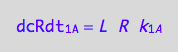
dcRdt_1_A = L*R*k_1_A
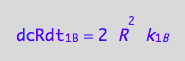
dcRdt_1_B = 2*R^2*k_1_B

 

The reverse reaction on A converts one molecule of RL to one of R so

dcRdt_2_A = dcRLdt_2_A;
eq3_2:= % | eq1_2c

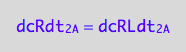
dcRdt_2_A = dcRLdt_2_A
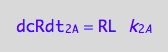
dcRdt_2_A = RL*k_2_A

 

The reverse reaction of B makes two molecules of R from one R2 so the conversion rate of R is a double of one of R2

dcRdt_2_B = 2* dcR2dt_2_B;
eq3_3:= % | eq1_4c

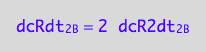
dcRdt_2_B = 2*dcR2dt_2_B
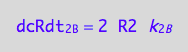
dcRdt_2_B = 2*R2*k_2_B

 

Therefore, the net conversion rate is

eq3_4:= eq3_1 | eq1_1c | eq1_3c | eq3_2 | eq3_3

dcRdt_N = - 2*k_1_B*R^2 - L*k_1_A*R + 2*R2*k_2_B + RL*k_2_A

 

 

 

 

 

Net conversion rate of RL

 

Sum all pertaining partial rates with respective signs

eq3_5:= dcRLdt_N = dcRLdt_1_A -dcRLdt_2_A

dcRLdt_N = dcRLdt_1_A - dcRLdt_2_A

dissociation rate is known

eq1_2c

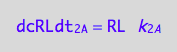
dcRLdt_2_A = RL*k_2_A

The forward (association reaction) makes same number of RL as uses R so

dcRLdt_1_A = dcRdt_1_A;
eq3_6:= % | eq1_1c

dcRLdt_1_A = dcRdt_1_A
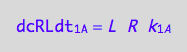
dcRLdt_1_A = L*R*k_1_A

 

Therefore, the net conversion rate is

eq3_7:= eq3_5 | eq1_2c | eq3_6

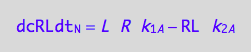
dcRLdt_N = L*R*k_1_A - RL*k_2_A

 

 

 

Net conversion rate of R2

 

Sum all pertaining partial rates with respective signs

eq3_8:= dcR2dt_N = dcR2dt_1_B - dcR2dt_2_B

dcR2dt_N = dcR2dt_1_B - dcR2dt_2_B

The dissociation rate is known

eq1_4c

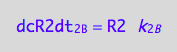
dcR2dt_2_B = R2*k_2_B

The association requires two molecules of R to make on R2 so

dcR2dt_1_B = dcRdt_1_B/2;
eq3_9:= % | eq1_3c

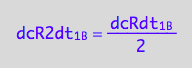
dcR2dt_1_B = dcRdt_1_B/2
dcR2dt_1_B = R^2*k_1_B

 

Therefore, the net conversion rate is

eq3_10:= eq3_8 | eq1_4c | eq3_9

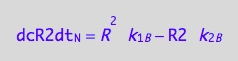
dcR2dt_N = R^2*k_1_B - R2*k_2_B

 

 

 

Back to Contents

 

 

 

 

 

4. Expression in terms of spin (monomer) concentrations

 

The Bloch-McConnell equations describe evolution of bulk magnetization of a sample, which is proportional to the number of spins found in every specific magnetic environment. A dimer contains two identical spins, therefore the amount of magnetization from spins in the environment of dimer is proportional to the doubled equilibrium concentration of a dimer.

 

 

 

 

Define new variables for concentrations and net conversion rates

 

We assign species as: R-1, R2-2, RL-3.

 

A monomeric receptor contains only one spin so everything is equivalent:

eq4_1a:= C_1 = R;
eq4_1b:= dC_1dt=dcRdt_N

C_1 = R
dC_1dt = dcRdt_N

 

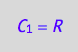
A dimer of receptror contains two spins

eq4_2a:= C_2 = R2*2;
eq4_2b:= dC_2dt = 2* dcR2dt_N

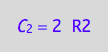
C_2 = 2*R2
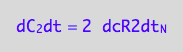
dC_2dt = 2*dcR2dt_N

 

A bound complex contains  one spin

eq4_3a:= C_3 = RL;
eq4_3b:= dC_3dt = dcRLdt_N

C_3 = RL
dC_3dt = dcRLdt_N

 

 

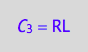
Express concentration of species in new concentration terms

solve(eq4_1a, R):
eq4_4:= R = %[1]

R = C_1

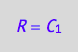
solve(eq4_2a, R2):
eq4_5:= R2 = %[1]

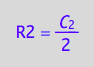
R2 = C_2/2

solve(eq4_3a, RL):
eq4_6:= RL = %[1]

RL = C_3

 

 

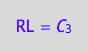
Obtain conversion rates in new concentrations

 

A spin in a monomeric receptor

eq4_1b | eq3_4;
eq4_7:= % | eq4_4 | eq4_5 | eq4_6

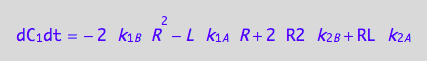
dC_1dt = - 2*k_1_B*R^2 - L*k_1_A*R + 2*R2*k_2_B + RL*k_2_A
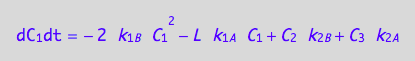
dC_1dt = - 2*k_1_B*C_1^2 - L*k_1_A*C_1 + C_2*k_2_B + C_3*k_2_A

 

 

A spin in a dimeric receptor

eq4_2b | eq3_10;
eq4_8:= % | eq4_4 | eq4_5 | eq4_6

dC_2dt = 2*R^2*k_1_B - 2*R2*k_2_B
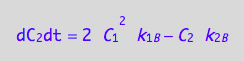
dC_2dt = 2*C_1^2*k_1_B - C_2*k_2_B

 

A spin in a bound complex

eq4_3b | eq3_7;
eq4_9:= % | eq4_4 | eq4_5 | eq4_6

dC_3dt = L*R*k_1_A - RL*k_2_A
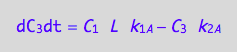
dC_3dt = C_1*L*k_1_A - C_3*k_2_A

 

 

 

Back to Contents

 

 

 

 

 

5. Final result

 

Summarize the derivation results

 

These are the differential equations governing  concentrations of spins experiencing environment of a monomer, C1,  a dimer, C2, and a receptor-ligand complex, C3.

eq4_7;
eq4_8;
eq4_9;

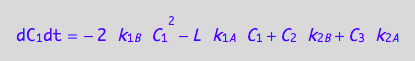
dC_1dt = - 2*k_1_B*C_1^2 - L*k_1_A*C_1 + C_2*k_2_B + C_3*k_2_A
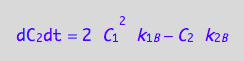
dC_2dt = 2*C_1^2*k_1_B - C_2*k_2_B
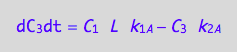
dC_3dt = C_1*L*k_1_A - C_3*k_2_A

where

eq4_1a;
eq4_2a;
eq4_3a;

C_1 = R
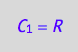
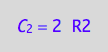
C_2 = 2*R2
C_3 = RL

 

 

 

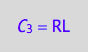
Prepare results for transfer to MATLAB

To avoid typing errors when transfering derived K matrix to MATLAB we enter it here and then directly test against derivation result. Then K matrix may be transfered to MATLAB by cut-and-paste of the MuPad output.

 

Restate the results

eq4_7;
eq4_8;
eq4_9;

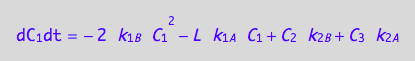
dC_1dt = - 2*k_1_B*C_1^2 - L*k_1_A*C_1 + C_2*k_2_B + C_3*k_2_A
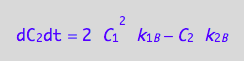
dC_2dt = 2*C_1^2*k_1_B - C_2*k_2_B
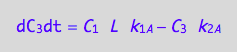
dC_3dt = C_1*L*k_1_A - C_3*k_2_A

 

Enter the K-matrix looking at the above results.

 

    Simple rules that allow catching mistakes in K matrix derivation:

   

   (1) a sum of each column should be zero (so each constant must appear with both positive and negative sign), and 

 

   (2) each row has to have complete pairs of constants (i.e., if k12

    appears there must be k21 in the same row with an opposite sign and so on). 

 

K:=matrix(3,3,[
[ (-2*k_1_B*C_1-k_1_A*L),   k_2_B,   k_2_A  ],
[   2*k_1_B*C_1,           -k_2_B,     0    ],
[               k_1_A*L,      0,    -k_2_A  ]
])

matrix([[- 2*C_1*k_1_B - L*k_1_A, k_2_B, k_2_A], [2*C_1*k_1_B, -k_2_B, 0], [L*k_1_A, 0, -k_2_A]])

Create P-column vector

P:=matrix(3,1,[ C_1, C_2, C_3])

matrix([[C_1], [C_2], [C_3]])

 

 

 

 

Check correctness of the entered K matrix by multiplying with P and comparing to the above equations:

 

Multiply K and P:

dCdt_manual_input:=K*P

matrix([[C_2*k_2_B + C_3*k_2_A - C_1*(2*C_1*k_1_B + L*k_1_A)], [2*C_1^2*k_1_B - C_2*k_2_B], [C_1*L*k_1_A - C_3*k_2_A]])

 

Collect right-hand-side parts of equations

dCdt_mupad:=matrix(3,1,[ rhs(eq4_7), rhs(eq4_8), rhs(eq4_9)])

matrix([[- 2*k_1_B*C_1^2 - L*k_1_A*C_1 + C_2*k_2_B + C_3*k_2_A], [2*C_1^2*k_1_B - C_2*k_2_B], [C_1*L*k_1_A - C_3*k_2_A]])

 

Compare derivation result to manual input

dCdt_mupad=dCdt_manual_input:
normal(%);
bool(%)

matrix([[- 2*k_1_B*C_1^2 - L*k_1_A*C_1 + C_2*k_2_B + C_3*k_2_A], [2*C_1^2*k_1_B - C_2*k_2_B], [C_1*L*k_1_A - C_3*k_2_A]]) = matrix([[- 2*k_1_B*C_1^2 - L*k_1_A*C_1 + C_2*k_2_B + C_3*k_2_A], [2*C_1^2*k_1_B - C_2*k_2_B], [C_1*L*k_1_A - C_3*k_2_A]])
TRUE

=> Great!

 

Use this K-matrix  (copy-paste output to MATLAB)

K;

matrix([[- 2*C_1*k_1_B - L*k_1_A, k_2_B, k_2_A], [2*C_1*k_1_B, -k_2_B, 0], [L*k_1_A, 0, -k_2_A]])

 

 

 

Back to Contents

 

 

 

 

 

Conclusions

 

Differential equations governing spin populations in U-R2 system have been derived. The K matrix has been prepared for transferring to MATLAB.

 

 

 

Back to Contents