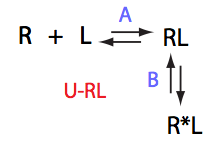

In this model the receptor-ligand complex isomerizes into an alternative conformation. This is a pure Koshland's induced-fit model (Koshland, 1966), where R cannot assume R* conformation in the absense of L.
One of the biophysical interaction mechanisms corresponding to this model is that RL represents a weak first-encounter complex eventually isomerizing into a tight-bound form.
NOTES ON TERMINOLOGY: Some authors refer to RL in this model as a 'transient' kinetic intermediate species. This is not correct because 'transient' implies that the RL complex completely interconverts into R*L with time. This is not the case. Ratio of R*L and RL concentrations is constant at any titration point under equilibrium conditions of NMR experiments. The RL complex is an intermediate species between the R and R*L in a sense that R*L cannot be formed directly because R* does not form in this model. However, RL is a genuine thermodynamic species with defined equilibrium concentration at any time during titration and after the titration is finished.
If a rapid-mixing experiment is performed instead of the equilibrium measurements (what NMR and ITC are) then, indeed, RL may be accumulating in excess of its equilibrium concentration in the beginning of the mixing reaction. In that context RL may be reffered as transiently populated intermediate species. However, independent of kinetics, if KB is not very large a measurable concentration of RL will be found after the reaction is complete (thus making 'transient kinetic intermediate' label entirely nonsensical for RL).
This is the simplest case, both transitions are in slow exchange. This case may be a model of an allosteric regulatory interaction where tight binding of the specific regulatory molecule at the binding site allows slow isomerization of the entire complex.
Report: summary_report
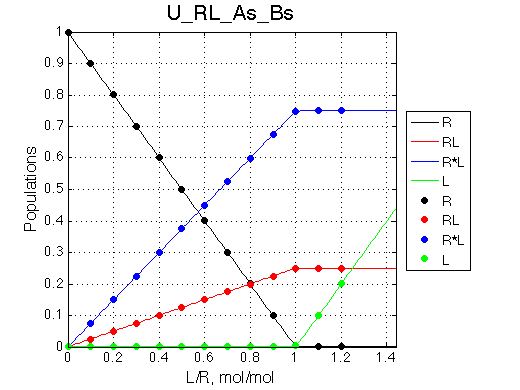
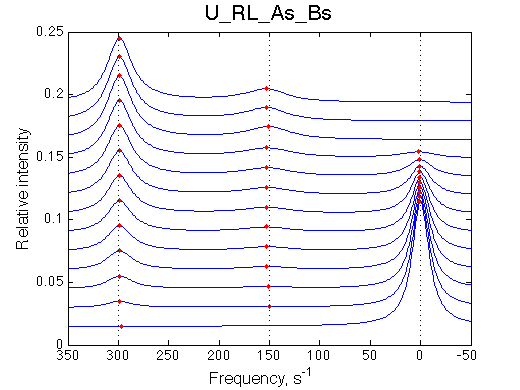
As the complex of R and L forms it is always split between RL and R*L with the equilibrium constant. In case KB >10 the peak of RL in the final spectra will unlikely be detectable with the practical signal-to-noise ratios.
Fast binding of L and slow isomerization of R*L is the model for formation of many receptor-ligand complexes when a low-affinity first-encounter complex with fast off-rate constant is formed between R and L following isomerization into a more thermodynamically stable species.
Report: summary_report

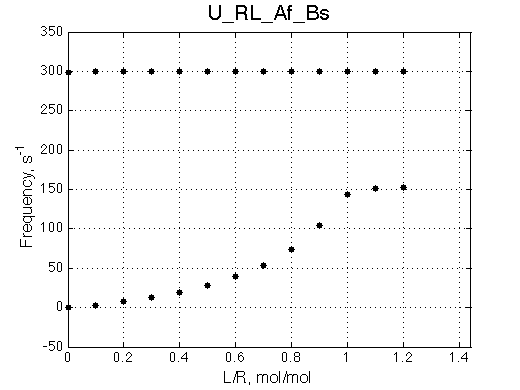
We can see that the R*L species at 300 s-1 is in slow exchange with the rest of the system. It gradually gains intensity as the titration progresses. The R and RL are in fast exchange with each other so one peak between R and RL positions is observed shifted accordingly to population ratio of R and RL. This shift is nonlinear if viewed on a chemical shift titration plot despite the single-site binding mechanism.
In this example I set KB=3 to still have RL complex peak observable at the end of titration. A more realistic example may be if KB is larger so RL peak is never observed. This is a situation when a disordered peptide binds to a protein receptor and becomes structured in the complex (see, for example, (Sugase et al. 2007)).
Simulate setup2 U_RL_Af_Bs2
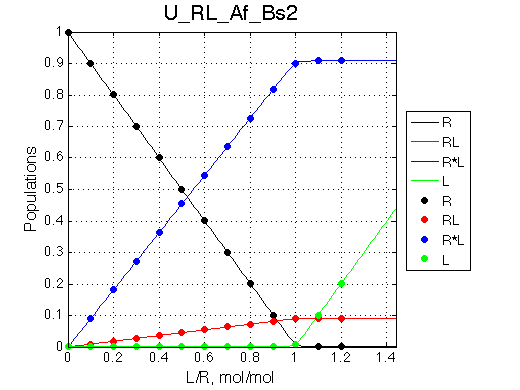
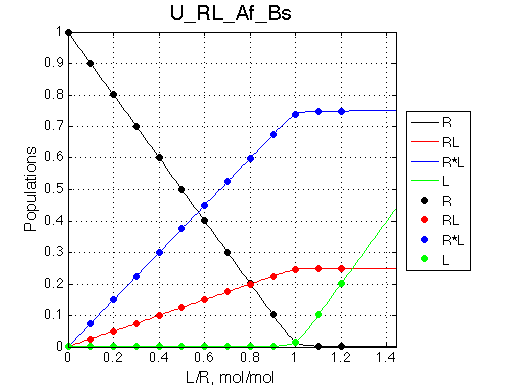
Here we assumed that the largest chemical shift difference occurs upon binding event (from R to RL) and readjustment of structure to R*L has less dramatic effect. This assumption is not necessary, I only want to emphasize the spectral changes we observe:
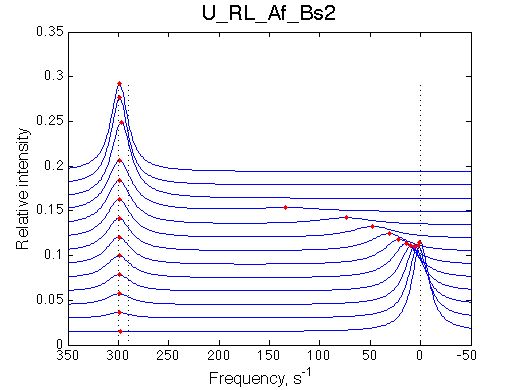
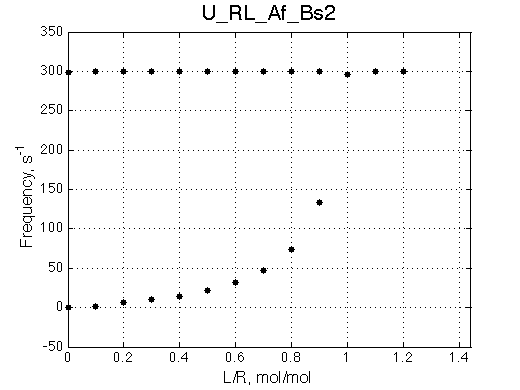
The most curious phenomenon is that the R peak is moving towards RL chemical shift in a nonlinear fashion and it disappears as the R*L peak gains intensity.
In this example the peak shifts towards growing peak of R*L which is due to purely accidental choice of the chemical shifts for the species. In the next simulation we re-position chemical shifts to illustrate that the fast exchange peak moves towards RL position even if it never becomes significantly populated.
Simulate setup2 U_RL_Af_Bs3
Here R is at 100/s, RL is at 300/s and R*L is 0/s
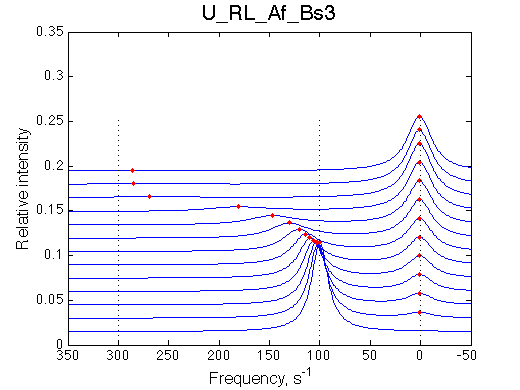
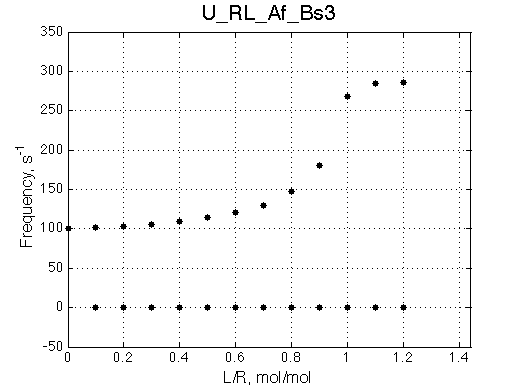
It must be noted that this behavior is also observed for systems with oligomerization of the free R (U_R2 model) so a concentration independence of free R peak position must be verified before interpreting the titration results.
Fast-exchange binding process followed by fast isomerization represents another common biophysical interaction mechanism with formation of first-encounter complex RL and fast readjustment into a final conformation R*L.
Simulate setup3 U_RL_Af_Bf
Report: summary_report
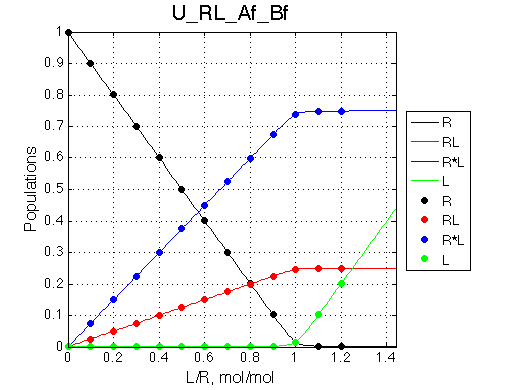
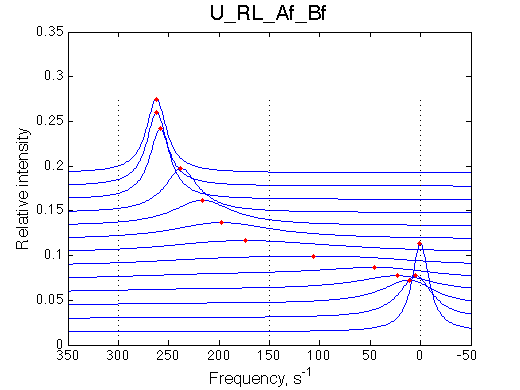
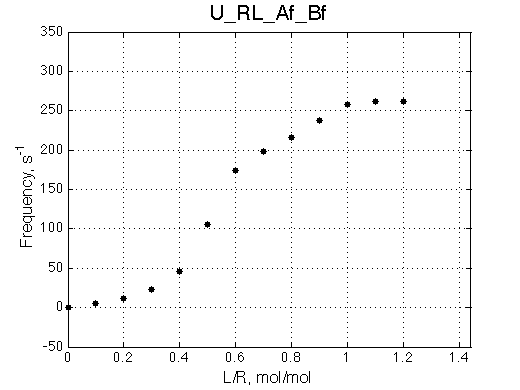
Bothprocesses are in fast exchange but overall we observe intermediate exchange regime.
It is worth noting that this model is a mirror image of the U_R model where isomerization occurs in the free receptor instead of receptor-ligand complex. With all the parameters of transitions identical, the U_R model produces line shapes that indicate much faster exchange regime:
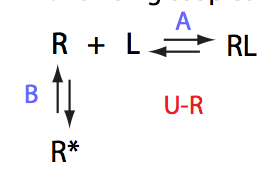
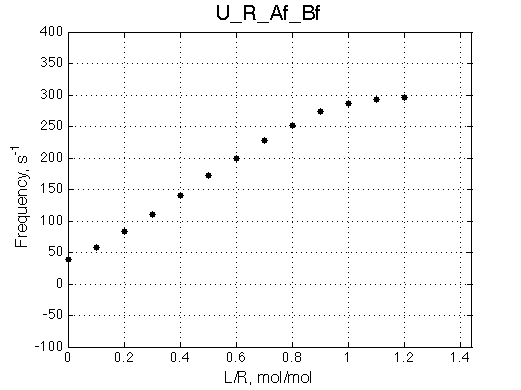
In order to drive U_RL model into similar overall faster exchange regime we have to increase off rate from 500/s to 1000/s for both isomerization and binding processes:
Simulate setup3 U_RL_Af_Bf2
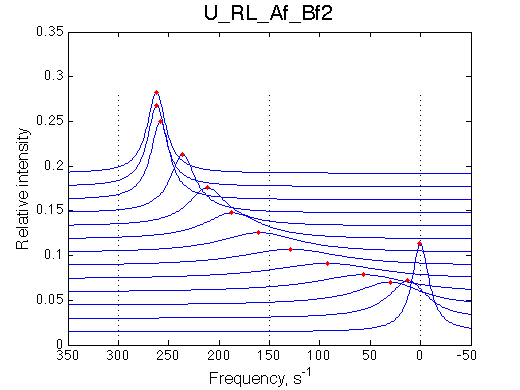

With both binding and isomerization in fast exchange we see one shifting averaged resonance and may propose the 2-site exchange (U model). Let's consider two arrangements of chemical shifts in this system:
| R, s-1 | RL, s-1 | R*L, s-1 | |
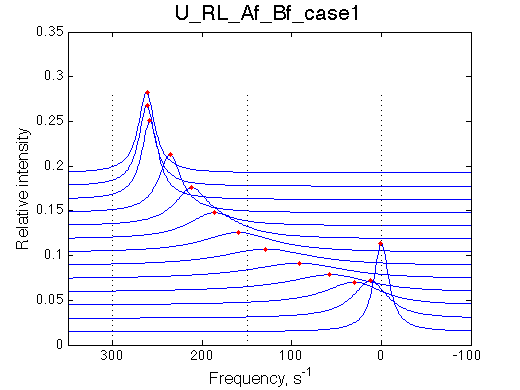
| case 1, U_RL_Af_Bf_case1.txt | 0 | 150 | 300 |
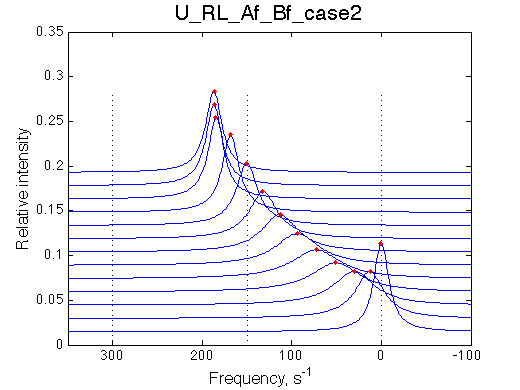
| case 2, U_RL_Af_Bf_case2.txt | 0 | 300 | 150 |
In both cases we will use k2=1000/s
Simulate setup3a U_RL_Af_Bf_case1
Simulate setup3a U_RL_Af_Bf_case2
| case 1 | case 2 |
 |
 |
[1] Kd: 2.03775e-07 +/- 1.1e-08 => Ka=1/Kd=5*106 |
1] Kd: 1.95389e-07 +/- 1.1e-08 |
Fit is adequate enough not to discard the 2-site model right away. In a slower exchange mode of case 1 (larger chemical shift sseparation between the end states) in the beginning of titration series 2-site model requires broader peaks with lower intensity, while at the end of titration the 2-site peaks must be sharper than U_RL produces. This is a similar pattern to what is observed with the U_R model spectra being fit to 2-site exchange. The discrepancy between the data in the fit there is much more remarkable but likely U_R and U_RL spectra may be easily confused and adequately fit by the opposite model. In case 2, when the exchange regime becomes faster (with smaller chemical shift separation), the fit becomes better so we have even less chance to detect deviation from the 2-state exchange process.
Note, that both fitting run result in apparent Ka of 5*106 , which is approximately what effective Ka for R*L is KA*(1+KB)=106(1+3)=4*106. It is remarkable, that 2-site fitting results in koff =200/s while both processes occur with 1000 s-1 rate constants.
This is the case of conformational equilibrium in the complex while initial binding occurs with high affinity and slow off-rate.
Simulate setup4.txt U_RL_As_Bf.txt
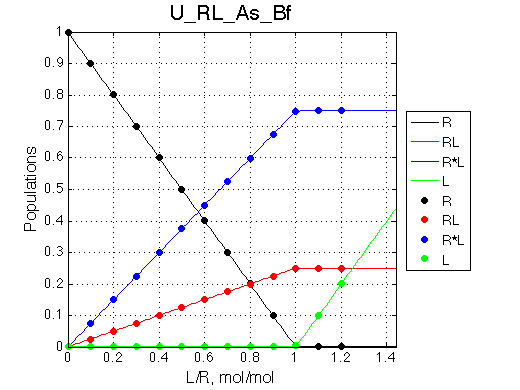
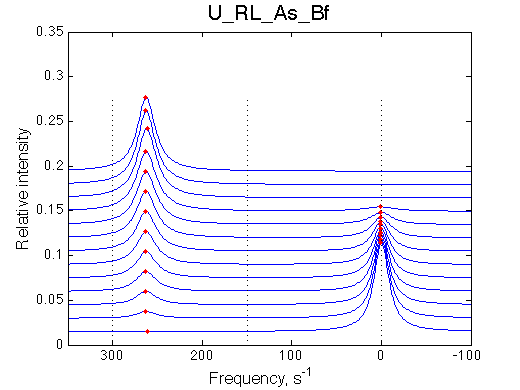
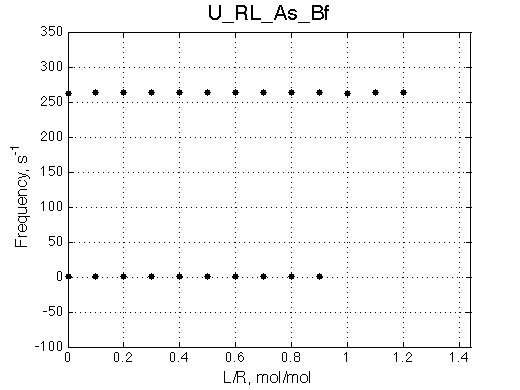
Fitting with 2-state model does not reveal much chance we have for detection of 3-state equilibrium if binding is slow.
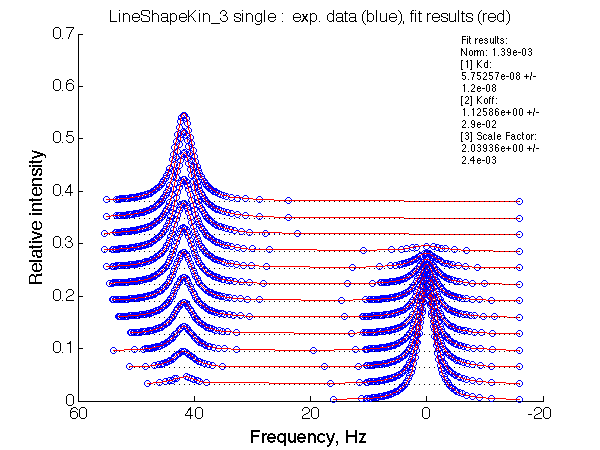
Slow exchange isomerization equilibrium gives us a chance to detect of 3-site mechanism if (1) binding is slow but isomerization equilibrium is not shifted too much towards R*L, or (2) binding is fast.
In case of fast isomerization and fast binding the spectra will deviate from 2-site mechanism if apparent exchange falls into intermediate regime.
Slow binding and fast isomerization do not give us a chance to detect 3-site exchange from this data alone.
Back to LineShapeKin Simulation Tutorial